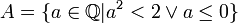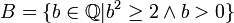Coupures de Dedekind

Coupure de Dedekind

En mathématiques, une coupure de Dedekind d'un ensemble totalement ordonné E est un couple (A,B) de sous-ensembles de E, lesquels forment à eux deux une partition de E, et où tout élément de A est inférieur à tout élément de B.

D'une certaine façon, une telle coupure conceptualise quelque chose qui se trouverait « entre » A et B, mais qui ne serait pas forcément un élément de E.

Les coupures de Dedekind furent introduites par Richard Dedekind comme moyen de construction de l'ensemble des nombres réels (en présentant de manière formelle ce qui se trouve « entre » les nombres rationnels).

Définition

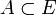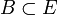Une coupure de Dedekind d’un ensemble totalement ordonné E se définit par un couple (A,B), où $A \subset E$ et $B \subset E$, et tels que :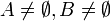

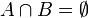
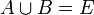
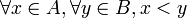
1. $A \ne \empty, B \ne \empty$
2. $A \cap B = \empty$
3. $A \cup B = E$
4. $\forall x \in A, \forall y \in B, x<y$
5. A ne possède pas un plus grand élément.

Les points 1, 2 et 3 posent que A et B réalisent une partition de E. Par conséquent, la définition de l'un détermine entièrement l'autre.

Le point 4 pose le partage des éléments de E dans ces deux parties. Il est possible de montrer que ce point équivaut à :

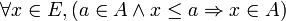• $\forall x \in E, (a\in A \land x\le a \Rightarrow x\in A)$ et
• $\forall y \in E, (b\in B \land y\ge b \Rightarrow y\in B)$.

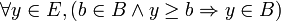Le point 5 permet d'associer à chaque élément de E, une coupure de Dedekind unique. Ainsi, si 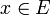$x \in E$, on lui associe la coupure 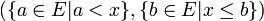$( \{ a\in E | a < x \} , \{ b\in E | x \le b \} )$, car il résulte de la définition que 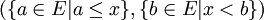$( \{ a\in E | a \le x \} , \{ b\in E | x < b\} )$ n'est pas une coupure de Dedekind.

Exemples

Construction des nombres réels

Si 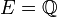$E=\mathbb Q$, l'ensemble des nombres rationnels, on peut considérer la coupure suivante :

$A=\{a\in\mathbb Q | a^2<2\lor a\le 0 \}$

$B = \{ b\in\mathbb Q | b^2\ge 2\land b>0 \}$

Cette coupure permet de représenter le nombre irrationnel 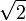$\sqrt{2}$ qui est ici défini à la fois par l'ensemble des nombres rationnels qui lui sont inférieurs et par celui des nombres rationnels qui lui sont supérieurs.

La prise en compte de toutes les coupures de Dedekind sur 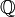$\mathbb Q$ permet une construction de l'ensemble des nombres réels $\mathbb R$ (voir l'article Construction des nombres réels).

Ordre sur les coupures de Dedekind

Soient (A,B) et (C,D) deux coupures de Dedekind de E. On définit un ordre sur l'ensemble des coupures de Dedekind de E en posant :

$(A,B)<(C,D) \Leftrightarrow A\subset C$.

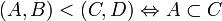Il est possible de montrer que l'ensemble des coupures de Dedekind de E muni de cet ordre possède la propriété de la borne supérieure, même si E ne la possède pas. En plongeant E dans cet ensemble, on le prolonge en un ensemble dont tout sous-ensemble possède une borne supérieure.

Voir aussi

• Richard Dedekind
• Nombre réel
• Nombre surréel
• Construction des nombres réels
• Suite de Cauchy

Ce document provient de « Coupure de Dedekind ».