Catégorie monoidale
- Catégorie monoidale
-
Catégorie monoïdale
En mathématiques, une catégorie monoïdale est une catégorie munie d'un bifoncteur qui généralise la notion de produit tensoriel de deux structures algébriques. Intuitivement, il s'agit de l'analogue, au niveau des catégories, de la notion de monoïde, c'est-à-dire que le bifoncteur joue le rôle d'une sorte de multiplication pour les objets de la catégorie.
Définition
Une catgéorie monoïdale est une catégorie 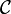 munie :
munie :
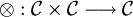
appelé produit tensoriel.
- D'un objet I appartenant à
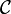 appelé objet unité.
appelé objet unité.
- D'une transformation naturelle α appelé associateur telle que pour tous objets A,B,C, αA,B,C soit un isomorphisme de
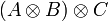 vers
vers 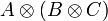 . Autrement dit, α est un isomorphisme naturel du foncteur
. Autrement dit, α est un isomorphisme naturel du foncteur 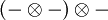 vers le foncteur
vers le foncteur 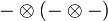 .
.
- De deux transformations naturelles λ,ρ telles que pour tout objet A, λ et ρ induisent des isomorphismes
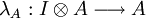 et
et 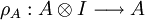 .
.
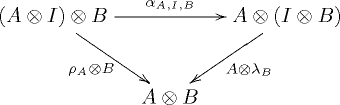
Les conditions de cohérence pour ces transformations naturelles s'expriment par la commutativité des diagrammes suivants:

Exemples
- Si k est un corps, la catégorie des k-espaces vectoriels munie du produit tensoriel usuel est une catégorie monoïdale.
- Plus généralement, si R est un anneau commutatif, la catégorie des R-modules munie du produit tensoriel usuel est une catégorie monoïdale.
- Si A est une algèbre, la catégorie des A-modules n'est pas une catégorie monoïdale en général. Il faut des conditions supplémentaires sur A, par exemple que A soit une algèbre de Hopf.
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégories : Théorie des catégories | Groupes quantiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Catégorie monoidale de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Catégorie monoïdale — En mathématiques, une catégorie monoïdale est une catégorie munie d un bifoncteur qui généralise la notion de produit tensoriel de deux structures algébriques. Intuitivement, il s agit de l analogue, au niveau des catégories, de la notion de… … Wikipédia en Français
Catégorie monoïdale symétrique — Catégorie monoïdale tressée En mathématiques, une catégorie monoïdale tressée est une catégorie monoïdale particulière, à laquelle on ajoute l analogue de la notion de commutativité. Définition formelle Soit une catégorie monoïdale. On note le… … Wikipédia en Français
Catégorie monoïdale tressée — En mathématiques, une catégorie monoïdale tressée est une catégorie monoïdale particulière, à laquelle on ajoute un analogue de la notion de commutativité. Définition formelle Soit une catégorie monoïdale. On note le produit tensoriel opposé à ,… … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Tenseur (mathématiques) — Pour l’article homonyme, voir Tenseur. Les tenseurs sont des objets mathématiques issus de l algèbre multilinéaire permettant de généraliser les scalaires et les vecteurs. On les rencontre notamment en analyse vectorielle et en… … Wikipédia en Français
Opérade — En algèbre générale, une opérade est une structure algébrique modélisant les propriétés (associativité, commutativité et autres relations) d une algèbre. Intuitivement, les éléments d une opérade correspondent à des opérations à plusieurs entrées … Wikipédia en Français
Opérades — Opérade En algèbre générale, une opérade est une structure algébrique modélisant les propriétés (associativité, commutativité et autres relations) d une algèbre. Intuitivement, les éléments d une opérade correspondent à des opérations à plusieurs … Wikipédia en Français
Algebre de Hopf — Algèbre de Hopf En mathématiques, une algèbre de Hopf, du nom du mathématicien Heinz Hopf, est une bialgèbre qui possède en plus une opération (l antipode) qui généralise la notion de passage à l inverse dans un groupe. Ces algèbres ont été… … Wikipédia en Français
Algebre de Hopf quasi-triangulaire — Algèbre de Hopf quasi triangulaire En mathématiques, une algèbre de Hopf H est dite quasi triangulaire s il existe un élément inversible qui vérifie : où … Wikipédia en Français
 munie :
munie :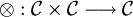
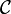 appelé objet unité.
appelé objet unité.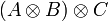 vers
vers 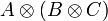 . Autrement dit, α est un isomorphisme naturel du foncteur
. Autrement dit, α est un isomorphisme naturel du foncteur 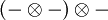 vers le foncteur
vers le foncteur 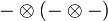 .
.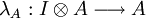 et
et 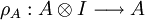 .
.

