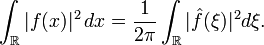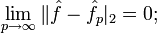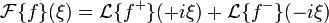- Transformee de Fourier
-
Transformée de Fourier
En analyse, la transformation de Fourier est un analogue de la théorie des séries de Fourier pour les fonctions non périodiques, et permet de leur associer un spectre en fréquences. On cherche ensuite à obtenir l'expression de la fonction comme « somme infinie » des fonctions trigonométriques de toutes fréquences qui forment son spectre. Une telle sommation se présentera donc sous forme d'intégrale. L'analyse non standard permet de la présenter sous forme d'une série et justifie le point de vue intuitif. Séries et transformation de Fourier constituent les deux outils de base de l'analyse harmonique.
Transformation de Fourier pour les fonctions intégrables
La transformée de Fourier
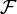 est une opération qui transforme une fonction intégrable sur
est une opération qui transforme une fonction intégrable sur  en une autre fonction, décrivant le spectre fréquentiel de cette dernière. Si
en une autre fonction, décrivant le spectre fréquentiel de cette dernière. Si 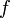 est une fonction intégrable sur
est une fonction intégrable sur  , sa transformée de Fourier est la fonction
, sa transformée de Fourier est la fonction 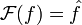 donnée par la formule :
donnée par la formule :Il est possible de choisir une définition alternative pour la transformée de Fourier. Ce choix est une affaire de convention dont les conséquences ne se manifestent (en général) que par des facteurs numériques. Par exemple, certains électroniciens utilisent ainsi :
avec t en secondes ν la fréquence (en s − 1).
Certains physiciens utilisent pour des raisons de symétrie avec la transformée de Fourier inverse :
avec t en secondes et ω la pulsation (en rad.s − 1). Cette définition n'est cependant pas adaptée au traitement des produits de convolution : à cause du facteur
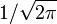 ,
, 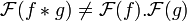 , à moins d'introduire un tel facteur dans la définition du produit de convolution.
, à moins d'introduire un tel facteur dans la définition du produit de convolution.L'ensemble de départ est l'ensemble des fonctions intégrables
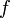 d'une variable réelle
d'une variable réelle 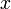 . L'ensemble d'arrivée est l'ensemble des fonctions d'une variable réelle
. L'ensemble d'arrivée est l'ensemble des fonctions d'une variable réelle  . Concrètement lorsque cette transformation est utilisée en traitement du signal, on notera volontiers t à la place de x et
. Concrètement lorsque cette transformation est utilisée en traitement du signal, on notera volontiers t à la place de x et 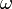 ou
ou 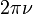 à la place de
à la place de  qui seront les variables respectives de temps et de pulsation ou de fréquence. On dira alors que
qui seront les variables respectives de temps et de pulsation ou de fréquence. On dira alors que 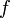 est dans le domaine temporel, et que
est dans le domaine temporel, et que  est dans le domaine fréquentiel.
est dans le domaine fréquentiel.En physique, la transformation de Fourier permet de déterminer le spectre d'un signal. Les phénomènes de diffraction donnent une image de l'espace dual du réseau, ils sont une sorte de « machine à transformation de Fourier » naturelle. Pour ces applications, les physiciens définissent en général la transformée directe avec un facteur
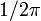 et la transformée de Fourier inverse sans aucun préfacteur.
et la transformée de Fourier inverse sans aucun préfacteur.Le cadre le plus naturel pour définir les transformées de Fourier est celui des fonctions intégrables. Toutefois, de nombreuses opérations (dérivations, transformée de Fourier inverse) ne peuvent être écrites en toute généralité. On doit à Plancherel l'introduction de la transformation de Fourier pour les fonctions de carré sommable, pour lesquelles la formule d'inversion est vraie. Puis la théorie des distributions de Schwartz permit de trouver un cadre parfaitement adapté.
La notation
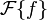 peut aussi être remplacée par F(f) ou TF(ƒ). Dans cet article, on utilisera exclusivement la première notation.
peut aussi être remplacée par F(f) ou TF(ƒ). Dans cet article, on utilisera exclusivement la première notation.Il est également d'usage dans certaines communautés scientifiques de noter
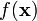 pour la fonction de départ et
pour la fonction de départ et 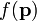 pour sa transformée, faisant ainsi correspondre à x, y, z les variables duales p, q, r. Cette notation est conforme à l'interprétation physique inspirée par la mécanique quantique : dualité entre position et moment. Cette notation n'est pas retenue ici.
pour sa transformée, faisant ainsi correspondre à x, y, z les variables duales p, q, r. Cette notation est conforme à l'interprétation physique inspirée par la mécanique quantique : dualité entre position et moment. Cette notation n'est pas retenue ici.On peut généraliser la définition de la transformée de Fourier à plusieurs variables, et même sur d'autres groupes que le groupe additif
 . Ainsi, on peut la définir sur le groupe additif
. Ainsi, on peut la définir sur le groupe additif 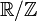 , c'est à dire sur les fonctions de période 1 — on retrouve ainsi les séries de Fourier — sur des groupes localement compacts, pas nécessairement commutatifs, et en particulier sur des groupes finis. Ces définitions font intervenir les groupes duaux.
, c'est à dire sur les fonctions de période 1 — on retrouve ainsi les séries de Fourier — sur des groupes localement compacts, pas nécessairement commutatifs, et en particulier sur des groupes finis. Ces définitions font intervenir les groupes duaux.Propriétés de la transformée de Fourier
Fonction Transformée de Fourier Linéarité 
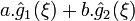
Contraction du domaine 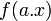
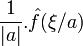
Translation temporelle 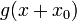
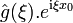
Modulation dans le domaine temporel 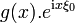
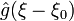
Produit de convolution 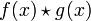
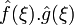
Dérivation 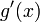
(voir conditions ci-dessous)
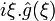
Symétrie réelle et paire réelle et paire réelle et impaire imaginaire pure et impaire imaginaire pure et paire imaginaire pure et paire imaginaire pure et impaire réelle et impaire gaussienne gaussienne - La contraction dans un domaine (temporel, spatial ou fréquentiel) implique une dilatation dans l'autre. Un exemple concret de ce phénomène peut être observé par exemple sur un gramophone. La lecture d'un 33 tours à 45 tours par minute implique une augmentation de la fréquence du signal audio (a<1), on contracte le signal audio dans le domaine temporel ce qui le dilate dans le domaine fréquentiel.
- Si la fonction f est à support bornée ( i.e, si
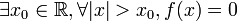 ) alors
) alors 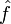 est à support infini. Inversement, si le support spectral de la fonction
est à support infini. Inversement, si le support spectral de la fonction 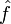 est borné alors f est à support infini.
est borné alors f est à support infini. - Si f est une fonction non-nulle sur un intervalle borné alors
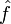 est une fonction non-nulle sur
est une fonction non-nulle sur 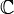 et inversement, si
et inversement, si 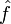 est non nulle sur un intervalle borné alors f est une fonction non nulle sur
est non nulle sur un intervalle borné alors f est une fonction non nulle sur 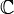 .
. - La transformée de Fourier de f est une fonction continue, de limite nulle à l'infini (théorème de Riemann-Lebesgue), notamment bornée par
- Par changement de variable on trouve des formules intéressantes lorsqu'on effectue une translation, dilatation du graphe de f.
- Supposons que la fonction
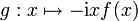 soit intégrable ; alors on peut dériver la formule de définition sous le signe d'intégration. On constate alors que la dérivée
soit intégrable ; alors on peut dériver la formule de définition sous le signe d'intégration. On constate alors que la dérivée 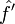 est la transformée de Fourier de g.
est la transformée de Fourier de g. - Si f est dérivable, de limite nulle à l'infini et si la dérivée de f est intégrable, alors
 est la transformée de Fourier de la dérivée de f .
est la transformée de Fourier de la dérivée de f .
On peut résumer les deux dernières propriétés : notons D l'opération
et M la multiplication par l'argument:
 .
.
Alors, si f satisfait des conditions fonctionnelles convenables,
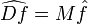 et
et 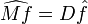 . Ces formules symétriques sont très belles, et aussi très importantes.
. Ces formules symétriques sont très belles, et aussi très importantes.On s'affranchira de ces conditions fonctionnelles en élargissant la classe des objets sur lesquelles opère la transformation de Fourier. C'est une des motivations de la définition des distributions.
Transformée de Fourier inverse
Si la transformée de Fourier de f est elle-même une fonction intégrable, la formule dite de transformation de Fourier inverse, opération notée
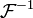 , est celle qui permet (sous conditions appropriées) de retrouver f à partir des données fréquentielles :
, est celle qui permet (sous conditions appropriées) de retrouver f à partir des données fréquentielles :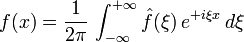 pour
pour 
Cette opération de transformation de Fourier inverse a des propriétés analogues à la transformation directe, puisque seuls changent le coefficient multiplicatif et le − i devenu i.
Dans le cas des définitions alternatives, la transformée de Fourier inverse devient:
- Définition en fréquence:
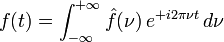 pour
pour 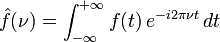
- Définition en pulsation:
 pour
pour 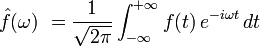
Preuve par la formule sommatoire de PoissonSoit h une fonction complexe définie sur
 et deux fois continûment différentiable. On suppose que h vérifie l'estimation
et deux fois continûment différentiable. On suppose que h vérifie l'estimationet que les deux premières dérivées de h sont intégrables sur
 . Alors la transformée de Fourier de h vérifie une estimation analogue
. Alors la transformée de Fourier de h vérifie une estimation analogueSoit y un nombre réel qui, pour le moment, est simplement un paramètre, et notons
-
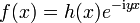 .
.
On vérifie que f a les mêmes propriétés fonctionnelles que h. Par conséquent, on peut appliquer la formule sommatoire de Poisson à f, avec la période 2π:
Mais le calcul de
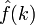 donne
donneOn peut donc réécrire la formule sommatoire de Poisson en termes de h, et il vient
On multiplie les deux membres de cette identité par eixy:
On remarque que les séries apparaissant de part et d'autre sont normalement convergentes pour la norme du maximum. On va donc pouvoir échanger la sommation et l'intégration par rapport à y sur l'intervalle [0,1].
A gauche, l'intégration par rapport à y ne laisse subsister qu'un seul terme, celui correspondant à n=0. A droite, on intègre par rapport à y et on effectue dans chaque intégrale le changement de variable y + k = ξ. On obtient ainsi la formule
On passe au cas général de la formule d'inversion de Fourier pour une fonction f intégrable ainsi que sa transformée de Fourier par une méthode de densité. On approche f par une suite de fonctions fp vérifiant les hypothèses fonctionnelles de la présente démonstration. On doit bien sûr supposer que les fp et leurs transformées de Fourier
 convergent vers leurs limites respectives f et
convergent vers leurs limites respectives f et  en norme
en norme 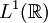 . On peut construire de telles approximations en tronquant f, c'est à dire en le remplaçant par 0 en dehors de l'intervalle [ − p,p], et en le régularisant par convolution. Si φ est une fonction deux fois continûment différentiable, d'intégrale 1, et à support borné, on pose φp(x) = pφ(px) et on convole la fonction tronquée f1[ − p,p] par φp. C'est une idée raisonnable d'utiliser ici le même paramètre p.Preuve par l'analyse non standard
. On peut construire de telles approximations en tronquant f, c'est à dire en le remplaçant par 0 en dehors de l'intervalle [ − p,p], et en le régularisant par convolution. Si φ est une fonction deux fois continûment différentiable, d'intégrale 1, et à support borné, on pose φp(x) = pφ(px) et on convole la fonction tronquée f1[ − p,p] par φp. C'est une idée raisonnable d'utiliser ici le même paramètre p.Preuve par l'analyse non standardSoit f est une fonction de classe
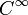 à support compact. Par le principe de transfert, on peut se contenter d'étudier le cas d'une fonction standard. Dans ce cas, il existe un réel infiniment grand T tel que pour tout réel | x | > T, f(x) = 0. Introduisons une base orthonormée totale de l'espace de Hilbert L2([ − T,T]) donnée par :
à support compact. Par le principe de transfert, on peut se contenter d'étudier le cas d'une fonction standard. Dans ce cas, il existe un réel infiniment grand T tel que pour tout réel | x | > T, f(x) = 0. Introduisons une base orthonormée totale de l'espace de Hilbert L2([ − T,T]) donnée par :Par le lemme de Parseval, on est en mesure d'écrire :
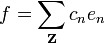 où
où 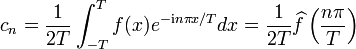
Plus explicitement, pour x standard :
La dernière égalité vient de ce que que le membre de gauche est standard, que la somme de Riemann s'effectue sur une partition de longueur infiniment petite(π / T), et donc que le membre de droite est la partie standard du membre intermédiaire. L'égalité recherchée est donc vraie pour toutes les fonctions standard de classe
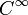 à support compact et tout x standard. Par le principe de transfert, elle est aussi vérifiée pour toutes les fonctions
à support compact et tout x standard. Par le principe de transfert, elle est aussi vérifiée pour toutes les fonctions 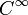 à support compact et tout x, puis par densité des fonctions
à support compact et tout x, puis par densité des fonctions 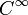 à support compact dans l'espace des fonctions intégrables, pour toutes les fonctions intégrables dont la transformée est intégrable et pour presque tout x.
à support compact dans l'espace des fonctions intégrables, pour toutes les fonctions intégrables dont la transformée est intégrable et pour presque tout x.Extension à l'espace
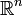
Notons
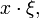 le produit scalaire dans
le produit scalaire dans 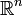 :
:Si f est une fonction intégrable sur
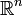 , sa transformée de Fourier est donnée par la formule
, sa transformée de Fourier est donnée par la formuleSi la transformée de Fourier de f est elle-même une fonction intégrable, on a alors la formule d'inversion:
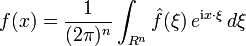 .
.
Transformation de Fourier pour les fonctions de carré sommable
Le théorème de Plancherel permet d'étendre la transformation de Fourier aux fonctions de carré sommable sur
 .
.On commence par un premier résultat.
Lemme — Soit h une fonction complexe deux fois continûment dérivable sur
 , qui vérifie l'estimation
, qui vérifie l'estimation-
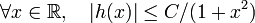 (où C est une constante),
(où C est une constante),
et dont les deux premières dérivées sont intégrables. Ceci implique que la transformée de Fourier
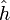 est bien définie et de carré intégrable. De plus, on a l'identité:Preuve par la formule sommatoire de Poisson
est bien définie et de carré intégrable. De plus, on a l'identité:Preuve par la formule sommatoire de PoissonOn reprend la formule établie ci-dessus dans la démonstration de la formule d'inversion de Fourier:
On prend le carré du module des deux membres, et on intègre sur l'intervalle [0,1] par rapport à y et sur l'intervalle [0,2π]:
On peut échanger l'ordre de la sommation et des deux intégrations dans l'expression ci-dessus, parce que les hypothèses faites sur h impliquent que les séries convergent normalement dans l'espace des fonctions continues de x et y, périodiques de période 2π en x et de période 1 en y. L'intégration en y du premier membre ne laisse subsister que les termes pour lesquels m et n sont égaux, et l'intégration en x du deuxième membre ne laisse subsister que les termes pour lesquels j et k sont identiques. Il reste donc:
Il suffit de faire dans le premier membre le changement de variable dans chaque intégrale x + 2πn = x' et dans le second le changement de variable dans chaque intégrale <\math>y+k=\xi</math>, et on obtient la formule:
Après changement de la variable muette x' en x, on obtient la formule annoncée.
Une fois démontrée dans le lemme ci-dessus la formule de Plancherel pour une classe de fonctions suffisamment régulières, on étend par densité la transformation de Fourier à tout
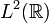 .Extension de la transformation de Fourier par densité
.Extension de la transformation de Fourier par densitéOn adopte encore les mêmes notations que dans la démonstration de la formule d'inversion de Fourier par la formule sommatoire de Poisson, donc φ est une fonction deux fois continûment différentiable, à support compact, et d'intégrale 1. On pose φp(x) = pφ(px).
Soit h une fonction de carré intégrable, et soit p un nombre entier quelconque. On définit
-
- hp = (h1[ − p,p]) * φp,
et on peut montrer le résultat suivant:
La démonstration utilise des techniques classiques d'approximation par régularisation.
D'autre part, les fonctions hp ont les propriétés nécessaires pour appliquer le lemme ci-dessus, et en particulier
Comme la suite
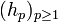 est de Cauchy dans l'espace
est de Cauchy dans l'espace 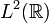 , la suite des transformées de Fourier
, la suite des transformées de Fourier 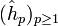 est aussi de Cauchy, donc elle converge. Sa limite, qu'on note
est aussi de Cauchy, donc elle converge. Sa limite, qu'on note 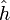 , ne dépend pas du choix de la suite d'approximations. En effet, si gp était une autre suite d'approximations convergeant vers h en moyenne quadratique, et satisfaisant les conditions fonctionnelles sous lesquelles on peut appliquer la formule sommatoire de Poisson, on aurait l'estimation
, ne dépend pas du choix de la suite d'approximations. En effet, si gp était une autre suite d'approximations convergeant vers h en moyenne quadratique, et satisfaisant les conditions fonctionnelles sous lesquelles on peut appliquer la formule sommatoire de Poisson, on aurait l'estimationqui tend vers 0 pour p tendant vers l'infini. Par conséquent
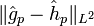 tend aussi vers 0 et on conclut que la limite de la suite
tend aussi vers 0 et on conclut que la limite de la suite 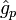 est bien
est bien 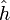 .
.On a ainsi le théorème de Plancherel:
Théorème de Plancherel — Soit f une fonction complexe sur
 et de carré sommable. Alors la transformée de Fourier de f peut être définie comme suit: pour tout p entier, on pose
et de carré sommable. Alors la transformée de Fourier de f peut être définie comme suit: pour tout p entier, on poseLa suite des transformées de Fourier
 converge dans
converge dans 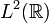 , et sa limite est la transformée de Fourier
, et sa limite est la transformée de Fourier  , c'est-à-dire
, c'est-à-direDe plus on a l'identité:
De façon similaire, si on pose
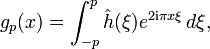 les gp convergent en moyenne quadratique vers fDémonstration du théorème de Plancherel
les gp convergent en moyenne quadratique vers fDémonstration du théorème de PlancherelL'identité suivante résulte du procédé d'extension décrit ci-dessus :
Considérons alors la suite de fonctions fp = f1[ − p,p]. En vertu du théorème de convergence dominée de Lebesgue pour les fonctions de carré sommable, la suite des fp converge en moyenne quadratique vers f, et par conséquent, on aura aussi
en d'autres termes,
 converge en moyenne quadratique vers
converge en moyenne quadratique vers  . La démonstration pour la formule d'inversion est analogue.
. La démonstration pour la formule d'inversion est analogue.Ainsi la transformation de Fourier-Plancherel définit un automorphisme de l'espace L2, qui est une isométrie, à condition de faire un changement d'échelle:
En physique, on interprète le terme
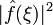 figurant sous l'intégrale comme une densité spectrale de puissance.
figurant sous l'intégrale comme une densité spectrale de puissance.
La définition de la transformation de Fourier-Plancherel est compatible avec la définition habituelle de la transformée de Fourier des fonctions intégrables. Sur l'intersection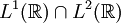 des domaines de définition, on montre à l'aide du théorème de convergence dominée de Lebesgue que les deux définitions coïncident.
des domaines de définition, on montre à l'aide du théorème de convergence dominée de Lebesgue que les deux définitions coïncident.Lien avec le produit de convolution
La transformation de Fourier a des propriétés très intéressantes liées au produit de convolution. Ainsi :
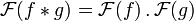
- Si
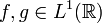 , alors
, alors 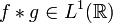 et
et 
- Si
 et
et 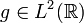 , alors
, alors 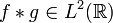 et
et 
Transformation de Fourier pour les distributions tempérées
Liens avec d'autres transformations
Lien avec les transformations de Laplace
La transformée de Fourier d'une fonction
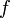 est un cas particulier de la transformée bilatérale de Laplace de cette même fonction définie par :
est un cas particulier de la transformée bilatérale de Laplace de cette même fonction définie par : 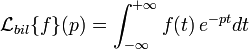 avec
avec 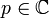
On constate alors que
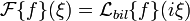 .
.
On peut également écrire ce lien en utilisant la transformée de Laplace "usuelle" par :où les fonctions
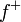 et
et 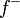 sont définies par :
sont définies par :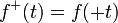 si t ≥ 0 et 0 sinon.
si t ≥ 0 et 0 sinon.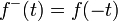 si t ≥ 0 et 0 sinon.
si t ≥ 0 et 0 sinon.
Lien avec les séries de Fourier
Parallèle formel
La transformée de Fourier est définie de façon semblable : la variable d'intégration x est remplacée par nΔx, n étant l'indice de sommation, et l'intégrale par la somme. On a alors
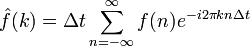 .
.
On trouvera quelques remarques à ce sujet dans Analyse spectrale.
Transformée
On utilise les variables normalisées suivantes :
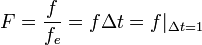 , Ω = eπF = 2πfΔt = ωδt | Δt = 1
, Ω = eπF = 2πfΔt = ωδt | Δt = 1Transformation de Fourier (analyse) Transformation inverse (synthèse) 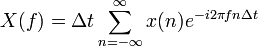
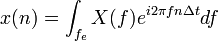
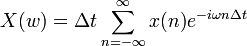
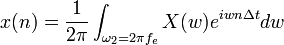

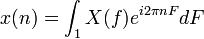
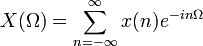
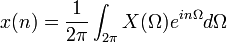
Références
- Jean-Michel Bony, Cours d'analyse, Editions de l'École Polytechnique
- Srishti D. Chatterji Cours d'analyse, Presses Polytechniques et Universitaires Romandes 1998 (ISBN 978-2880743468 )
Voir aussi
- Densité spectrale
- Densité spectrale de puissance
- Produit de convolution
- Transformée de Fourier rapide
- Transformée de Fourier discrète
- Transformée de Laplace
- Bispectre
Lien externe
- Portail des mathématiques
Catégories : Théorie de l'intégration | Mécanique ondulatoire | Spectroscopie | Théorie de Fourier | Transformée
Wikimedia Foundation. 2010.


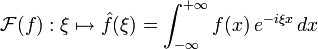
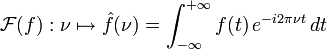
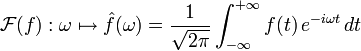
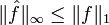
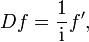
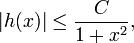

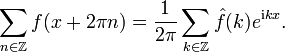
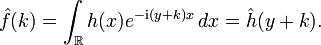
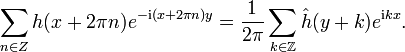

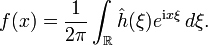
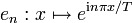
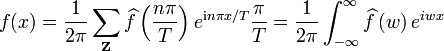
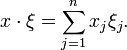
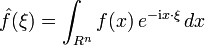
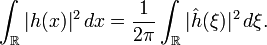
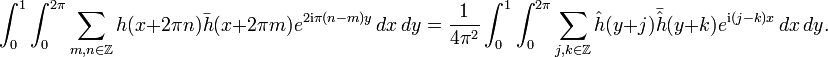
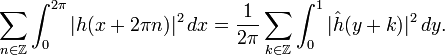

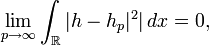
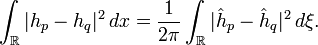
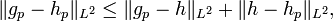
![f_p(x)=(f 1_{[-p,p]})(x)=\begin{cases}f(x) &\text{si } |x|\le p,\\0&\text{sinon}.\end{cases}](/pictures/frwiki/53/5f11b21e8e294f24b015189b4cd4636d.png)