- Theoreme de Radon
-
Théorème de Radon
Le théorème de projection de Radon établit la possibilité de reconstituer une fonction réelle à deux variables (assimilable à une image) à l'aide de la totalité de ses projections selon des droites concourantes. L'application la plus courante de ce théorème est la reconstruction d'images médicales en tomodensitométrie, c'est-à-dire dans les scanneurs à rayon X. Il doit son nom au mathématicien Johann Radon.
En pratique, il est impossible de disposer de toutes les projections d'un objet solide, seulement un échantillonnage. Mais il existe des méthodes pour combler ce manque d'information conformément à ce que l'on sait a priori sur l'image, par exemple les méthodes d'entropie maximale (voir théorème de Cox-Jaynes).
Transformée de Radon
La transformée de Radon est la formulation mathématique d'une projection. La transformée de Radon d'une fonction de deux variables f est donné par l'intégrale double selon une direction
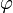 :
: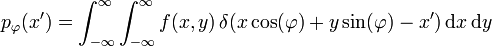
Où δ(x) est l'impulsion de Dirac.
Dans le cas où x' et
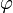 sont discrets, la transformée de Radon est équivalente à la transformée de Hough pour une droite.
sont discrets, la transformée de Radon est équivalente à la transformée de Hough pour une droite.Transformée inverse de Radon
La reconstruction de la fonction f en coordonnées polaires peut alors être réalisée à l'aide de la transformée inverse de Radon:
![\hat{f}(r,\theta)=\int_{-\infty}^{\infty} \mathcal{F}^{-1}[|\omega
|]*p_{\varphi}(x')\,\mathrm d\varphi](/pictures/frwiki/56/8d2a4d19c9737c9a921a126fe28c9e37.png)
Où
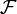 est la transformée de Fourier. La transformée inverse de Radon consiste à filtrer toutes les projections et à les propager sur toute l'image dans la même direction où ils avaient été projetés ; d'où le nom « reconstruction par rétroprojection filtrée » parfois aussi utilisé.
est la transformée de Fourier. La transformée inverse de Radon consiste à filtrer toutes les projections et à les propager sur toute l'image dans la même direction où ils avaient été projetés ; d'où le nom « reconstruction par rétroprojection filtrée » parfois aussi utilisé.- Portail des mathématiques
Catégories : Théorie de la mesure | Théorème de mathématiques | Radiologie
Wikimedia Foundation. 2010.

