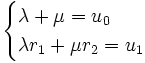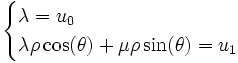- Suite récurrente linéaire d'ordre 1
-
Suite récurrente linéaire
En mathématiques, on appelle suite récurrente linéaire d’ordre p, toute suite à valeurs dans un corps K (généralement
 ou
ou  ) définie pour tout
) définie pour tout 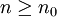 par la relation de récurrence suivante :
par la relation de récurrence suivante :a0, a1, …ap − 1 étant p scalaires fixés de K (a0 non nul), pour tout
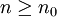 , on a
, on aUne telle suite est entièrement déterminée par la donnée des p premiers termes de la suite et par la relation de récurrence.
Les suites récurrentes linéaires d’ordre 1 s’appellent plus simplement des suites géométriques de raison a0. Concernant les suites récurrentes linéaires d'ordre 2, notons qu'on peut exprimer leur terme général sans avoir recours à la récurrence, plus précisément en utilisant seulement les deux premiers termes, quelques valeurs constantes, quelques opérations élémentaires de l'arithmétique (addition, soustraction, multiplication, exponentielle) et les fonctions sinus et cosinus. Une des suites de ce type est la très célèbre suite de Fibonacci qui peut s'exprimer à partir de puissances faisant intervenir le nombre d'or. L’étude des suites récurrentes linéaires d’ordre p fait appel à la notion d’espace vectoriel et au calcul matriciel.
Sommaire
Suite récurrente linéaire d’ordre 1
- Voir article détaillé : Suite géométrique
Si la relation de récurrence est
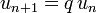 , le terme général est
, le terme général est 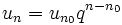
Suite récurrente linéaire d’ordre 2
a et b étant deux scalaires fixés de K avec b non nul, la relation de récurrence est
- un + 2 = aun + 1 + bun (R)
On va prouver que le terme général d'une telle suite est
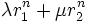 si r1 et r2 sont deux racines distinctes du polynôme X2 − aX − b
si r1 et r2 sont deux racines distinctes du polynôme X2 − aX − b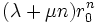 si r0 est racine double du polynôme X2 − aX − b
si r0 est racine double du polynôme X2 − aX − b pour une suite réelle quand ρeiθ et ρe − iθ sont les deux racines complexes du polynôme X2 − aX − b
pour une suite réelle quand ρeiθ et ρe − iθ sont les deux racines complexes du polynôme X2 − aX − b
On ne perd rien à la généralité de la suite en supposant que celle-ci est définie sur tout
 et pas seulement à partir de n0. En effet, si une suite (u) n’est définie qu’à partir de n0, elle induit la création d’une suite (v) définie sur
et pas seulement à partir de n0. En effet, si une suite (u) n’est définie qu’à partir de n0, elle induit la création d’une suite (v) définie sur  en posant
en posant  .
.L’idée est alors de rechercher des suites géométriques vérifiant la récurrence (R). C’est-à-dire chercher des scalaires r tels que la suite
 vérifie (R). On démontre aisément que ce problème équivaut à résoudre l’équation du second degré
vérifie (R). On démontre aisément que ce problème équivaut à résoudre l’équation du second degré 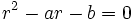 . Le polynôme
. Le polynôme 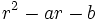 est alors appelé le polynôme caractéristique de la suite. Son discriminant est
est alors appelé le polynôme caractéristique de la suite. Son discriminant est 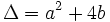 . Il faudra alors distinguer plusieurs cas, selon que le nombre de racines du polynôme caractéristique.
. Il faudra alors distinguer plusieurs cas, selon que le nombre de racines du polynôme caractéristique.Si le polynôme possède deux racines distinctes
Soient r1 et r2 les deux racines distinctes. Les suites
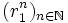 et
et 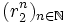 vérifient (R) ainsi que toute suite dont le terme général serait
vérifient (R) ainsi que toute suite dont le terme général serait 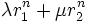 (cela tient au caractère linéaire de la récurrence). A-t-on alors trouvé toutes les suites vérifiant (R) ? Une suite vérifiant (R) étant entièrement déterminée par la donnée de u0 et u1, il suffit de prouver que l’on peut toujours trouver λ et μ solutions du système
(cela tient au caractère linéaire de la récurrence). A-t-on alors trouvé toutes les suites vérifiant (R) ? Une suite vérifiant (R) étant entièrement déterminée par la donnée de u0 et u1, il suffit de prouver que l’on peut toujours trouver λ et μ solutions du systèmeOr ce système a pour déterminant r2 − r1 non nul. Il est donc toujours possible d’exprimer une suite vérifiant (R) comme combinaison linéaire des suites
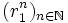 et
et 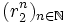
Cette situation se produit pour toute suite à valeurs réelles pour laquelle le discriminant
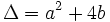 est strictement positif, ou pour toute suite à valeurs complexes pour laquelle le discriminant est non nul.
est strictement positif, ou pour toute suite à valeurs complexes pour laquelle le discriminant est non nul.Si le polynôme possède une racine double
Si le discriminant est nul, le problème est tout autre car on ne trouve qu’une seule valeur r0, donc une seule famille de suites géométriques
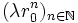 vérifiant (R) . L’idée consiste alors à rechercher les suites
vérifiant (R) . L’idée consiste alors à rechercher les suites 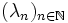 telles que, pour tout entier n,
telles que, pour tout entier n, 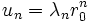 avec
avec 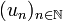 vérifiant (R). Cette méthode s’appelle la méthode de variation de la constante. On s’assure d’abord de l’existence de la suite
vérifiant (R). Cette méthode s’appelle la méthode de variation de la constante. On s’assure d’abord de l’existence de la suite 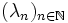 en vérifiant que r0 n’est jamais nul . La relation de récurrence sur
en vérifiant que r0 n’est jamais nul . La relation de récurrence sur 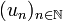 se traduit par une relation de récurrence sur
se traduit par une relation de récurrence sur 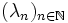 :
:En utilisant ensuite le fait que a2 + 4b = 0 et que
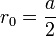 , on obtient la relation caractéristique de toute suite arithmétique :
, on obtient la relation caractéristique de toute suite arithmétique :- λn + 2 − λn + 1 = λn + 1 − λn
La suite
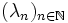 est donc une suite arithmétique de terme général
est donc une suite arithmétique de terme général- λn = λ + μn.
Les suites
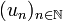 vérifiant (R) ont alors pour terme général :
vérifiant (R) ont alors pour terme général :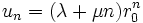 .
.
Ce résultat s'applique pour des suites à valeurs réelles ou complexes pour lesquelles le discriminant du polynôme caractéristique est nul.
Si le polynôme ne possède pas de racine réelle
C'est le cas pour les suites à valeurs réelles pour lesquelles le discriminant du polynôme caractéristique est strictement négatif. L’équation du second degré possède alors dans
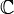 deux racines conjuguées.
deux racines conjuguées.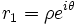 et
et 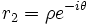 .
.
Les suites de terme général
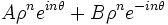 sont des suites complexes vérifiant (R). Parmi celles-ci, celles pour lesquelles A et B sont conjugués, sont des suites réelles . Donc les suites de terme général
sont des suites complexes vérifiant (R). Parmi celles-ci, celles pour lesquelles A et B sont conjugués, sont des suites réelles . Donc les suites de terme généralsont des suites réelles vérifiant (R) (on a pris A = λ / 2 − iμ / 2). A-t-on alors trouvé toutes les suites vérifiant (R) ? Une suite vérifiant (R) étant entièrement déterminée par la donnée de u0 et u1, il suffit de prouver que l’on peut toujours trouver λ et μ solutions du système
Or ce système a pour déterminant ρsin(θ) non nul. Il est donc toujours possible d’exprimer une suite vérifiant (R) comme combinaison linéaire des suites
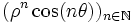 et
et 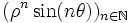 .
.Suite récurrente d’ordre p
Sous-espace vectoriel de dimension p
Si on appelle (Rp) la relation de récurrence :
- pour tout entier n,
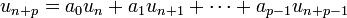
et si on appelle
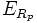 , l’ensemble des suites à valeurs dans K et vérifiant (Rp), on démontre que
, l’ensemble des suites à valeurs dans K et vérifiant (Rp), on démontre que 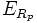 est un sous-espace vectoriel de l’ensemble des suites à valeurs dans K. Cela tient à la linéarité de la relation de récurrence.
est un sous-espace vectoriel de l’ensemble des suites à valeurs dans K. Cela tient à la linéarité de la relation de récurrence.De plus, ce sous espace vectoriel est de dimension p. En effet, il existe un isomorphisme d’espace vectoriel entre
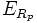 et l’ensemble
et l’ensemble 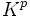 : à chaque suite (u) de
: à chaque suite (u) de 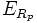 , on associe le p_uplet
, on associe le p_uplet  . Il suffit alors de connaître une famille libre de p suites vérifiant (Rp), l’ensemble
. Il suffit alors de connaître une famille libre de p suites vérifiant (Rp), l’ensemble 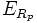 est alors engendré par cette famille libre.
est alors engendré par cette famille libre.Terme général
La recherche du terme général et des suites particulières s’effectue en travaillant sur Kp . À chaque suite
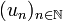 on associe la suite
on associe la suite  telle que
telle queLa relation de récurrence sur
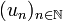 induit une relation de récurrence sur
induit une relation de récurrence sur 
- Un + 1 = AUn où

Le terme général de la suite U est alors déterminé par
- Un = AnU0
Le problème semble alors terminé. Mais la réelle difficulté consiste alors à calculer An... On préfère plutôt déterminer une base de
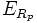 .
.Recherche d'une base
Le polynôme caractéristique de la matrice A est
 . Ce n'est pas un hasard si on le retrouve pour caractériser les suites
. Ce n'est pas un hasard si on le retrouve pour caractériser les suites  vérifiant Rp.
vérifiant Rp.On note f la transformation linéaire qui, à une suite
 associe la suite
associe la suite 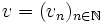 définie par vn = un + 1. La condition u vérifie Rp se traduit alors par P(f)(u) = 0. L'ensemble
définie par vn = un + 1. La condition u vérifie Rp se traduit alors par P(f)(u) = 0. L'ensemble 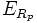 est donc le noyau de P(f). Si P est un polynôme scindé dans K (ce qui est toujours vrai si
est donc le noyau de P(f). Si P est un polynôme scindé dans K (ce qui est toujours vrai si 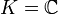 ), il existe k racines
), il existe k racines 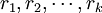 et k exposants
et k exposants  tel que
tel que 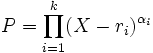 . Le noyau de P(f) est alors la somme directe des noyaux des
. Le noyau de P(f) est alors la somme directe des noyaux des 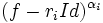 . Il suffit donc de trouver une base de chacun de ces noyaux pour déterminer une base de
. Il suffit donc de trouver une base de chacun de ces noyaux pour déterminer une base de 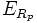 .
.On peut montrer que toute suite de terme général
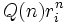 est élément du noyau de
est élément du noyau de 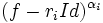 pour peu que le degré de Q soit inférieur strictement à αi. Cette démonstration se fait par récurrence sur αi. Comme les suites
pour peu que le degré de Q soit inférieur strictement à αi. Cette démonstration se fait par récurrence sur αi. Comme les suites 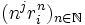 , pour j = 0 à αi − 1 forment une partie libre de αi éléments, la famille de toutes les suites
, pour j = 0 à αi − 1 forment une partie libre de αi éléments, la famille de toutes les suites 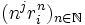 , pour j = 0 à αi − 1 et pour i = 1 à k forme une famille libre de
, pour j = 0 à αi − 1 et pour i = 1 à k forme une famille libre de  éléments de
éléments de 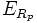 (de dimension p) donc une base de
(de dimension p) donc une base de 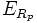 . Les éléments de
. Les éléments de 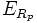 sont donc des sommes de suites dont le terme général est
sont donc des sommes de suites dont le terme général est 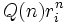 avec degré de Q strictement inférieur à αi.
avec degré de Q strictement inférieur à αi.Retour à la récurrence d'ordre 2
Si le polynôme caractéristique se scinde en (X − r1)(X − r2) alors les polynômes Q sont de degré 0 et les éléments de
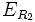 sont des suites dont le terme général est
sont des suites dont le terme général est 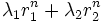 .
.Si le polynôme caractéristique se scinde en (X − r0)2 alors les polynômes Q sont de degré 1 et les éléments de
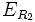 sont des suites dont le terme général est
sont des suites dont le terme général est 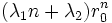 .
.- Portail des mathématiques
Catégories : Mathématiques élémentaires | Suite | Algèbre linéaire
Wikimedia Foundation. 2010.