- Méthode De Bessel
-
Méthode de Bessel
La méthode de Bessel est une méthode focométrique de détermination expérimentale de la focale d'une lentille convergente.
Sommaire
Principe
On considère une lentille mince convergente de focale f', de centre O, de foyers image F' et objet F.
Soient D, la distance entre l'objet A (sur l'axe optique) et l'écran (où l'on visualise l'image A'), et d, la distance entre les deux positions de la lentille qui assurent la conjugaison de A et A', (c’est-à-dire la netteté de l'image sur l'écran). On peut déduire la valeur de la focale f' par la formule:
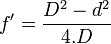
 Schéma animé sur la méthode de Bessel
Schéma animé sur la méthode de Bessel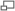
Explication
Formules de conjugaison
Les formules de conjugaison de Descartes donnent une relation entre les positions sur l'axe optique d'un objet A et de son image A' par rapport au centre optique O. Elles sont exprimées avec des distances algébriques.
Soit A un point de l'axe optique et A' son image par la lentille :
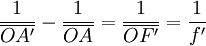
On suppose que A' est réelle (c’est-à-dire projetable sur un écran):
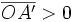 .
.Il faut pour cela que A soit placé sur l'axe optique à une distance
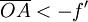 .
.Formation d'une image réelle à partir d'un objet réel
On fixe
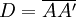 , la distance entre l'objet (A) et l'écran (A') et on pose
, la distance entre l'objet (A) et l'écran (A') et on pose 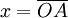 et
et 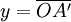 , donc
, donc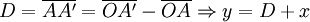 .
.Les relations de conjugaison se réécrivent:
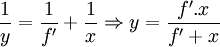 .
.La combinaison des deux précédentes équations donne bien une équation du second ordre en x: x2 + D.x + f'.D = 0
Cette équation n'a de solution réelle que si
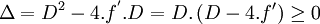
Aussi, il faut que
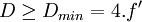
Positions respectives de l'image et de l'objet
Si D > Dmin, alors Δ > 0: il y a deux solutions réelles (il existe alors deux positions de la lentille qui permettent de conjuguer A et A').
Les solutions sont:
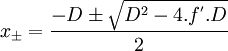 . Aussi, ces deux positions possibles de l'objet sont éloignées de
. Aussi, ces deux positions possibles de l'objet sont éloignées de 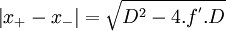 .
.Cette distance est aussi la distance entre les deux positions de la lentille qui assurent la conjugaison de A et A' :
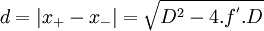 .
.En élevant au carré, on trouve la formule:
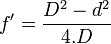
Remarque
La méthode de Silbermann apparaît comme un cas particulier de la méthode de Bessel, celui où la position de la lentille est unique (soit d=0).
Voir aussi
Articles connexes
Liens externes
- Portail de la physique
Catégorie : Lentille
Wikimedia Foundation. 2010.
