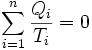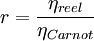Machine Thermique

Machine thermique

Une machine thermique est un mécanisme permettant d'effectuer un travail à l'aide d'une source de chaleur. La théorie des machines thermiques s'attache à la description et à l'étude physique de certains systèmes thermodynamiques qui permettent de transformer l'énergie thermique en énergie mécanique, et vice versa. Fondée au milieu du XIXe siècle, elle s'appuie sur la thermodynamique, et en particulier sur ses deux premiers principes.

Naissance

C'est le désir de mettre en équation les machines thermiques (avec Carnot notamment) qui est à l'origine de la thermodynamique et en particulier du premier et du second principe. Selon Feynman dans son Cours de Physique, il s'agirait d'un des rares cas où les sciences de l'ingénieur ont permis une avancée importante de la physique fondamentale.

Fondements théoriques

Premier principe

Le premier principe de la thermodynamique relie le travail mécanique à la chaleur et à l'énergie mécanique d'un système. Si le système est capable d'effectuer des cycles, la variation d'énergie entre deux cycles successifs est nulle :

ΔE = W + Q = 0

Cycle d'une machine ditherme

Le travail et la chaleur étant liées, on peut, en contrôlant l'une de ces variables, influencer l'autre. Dans le cas général, le fluide des machines thermiques est au contact de sources thermiques, de différentes températures T₁,T₂,...,T_n qui fournissent des chaleurs Q₁,Q₂,...,Q_n; et reçoivent un travail W. On algébrise ces valeurs vu du fluide : Q_i est positif si le transfert s'effectue de la source vers le fluide, négatif dans le cas contraire.

On nommera la machine thermique en fonction du signe de W :

• moteur si W < 0.
• récepteur si W > 0; catégorie dans laquelle on distingue :
  • les pompes à chaleur si le but de la machine est de « réchauffer » la source chaude.
  • les réfrigérateurs si le but est de refroidir la source froide.

Par exemple, un réfrigérateur est en contact avec deux sources de chaleur : une source dite froide qui est l'intérieur du réfrigérateur et une source dite chaude qui est l'atmosphère extérieur, il reçoit un travail d'origine électrique qui fait fonctionner une pompe permettant la circulation du fluide thermique. Dans cet exemple Q_F est positif (on extrait de l'énergie du réfrigérateur), Q_C est négatif (on « réchauffe l'air ») et W est positif (le moteur électrique donne de l'énergie au fluide en le faisant circuler).

Inégalité de Clausius

Le premier principe, s'il pose les bases des machines thermiques, néglige une partie de leur étude : en effet, le second principe de la thermodynamique, qui traite de l'entropie, s'oppose à des aberrations tels que le « mouvement perpétuel ». Il permet également, sous la forme de l'inégalité de Clausius, de prédire l'efficacité théorique maximale d'une machine.

La variation d'entropie se répartit de la façon suivante :

ΔS_cycle = S_echangee + S_creee

Or, puisque S est une fonction d'état (dS est une différentielle exacte), on a :

ΔS_cycle = 0

Dans de nombreux cas,

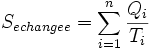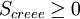$S_{echangee}=\sum_{i=1}^{n} \frac{Q_{i}}{T_{i}}$ et $S_{creee} \geq 0$ (second principe)

d'où l'inégalité de Clausius : $\sum_{i=1}^{n} \frac{Q_{i}}{T_{i}} \leq 0$.

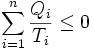Dans le « cas réversible », hypothétique, où S_creee = 0, on obtient l'égalité de Clausius-Carnot :

$\sum_{i=1}^{n} \frac{Q_{i}}{T_{i}} = 0$

On peut à partir de cette égalité limite établir l'efficacité théorique maximale que l'on peut espérer avec la machine.

Rendement, efficacité d'une machine thermique

L'efficacité d'une machine thermique, qui est une grandeur sans dimension, peut s'exprimer qualitativement comme :

« $|\frac{ce \; qui \; est \; utile}{ce \; que \; l'on \;fournit}|$ »

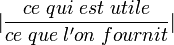De manière plus rigoureuse, en termes d'énergie,

$\eta = |\frac{\Delta E_{fournie}}{\Delta E_{consommee}}|$.

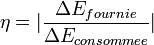L'efficacité théorique maximale d'une machine thermique ditherme est réalisée par un cycle entièrement réversible constitué de deux isothermes et deux adiabatiques, appelé cycle de Carnot. Cette limite ne dépend que des températures des sources de chaleur et est donc indépendante de la technologie utilisée.

Il est aussi possible de définir le rendement r d'une machine thermique comme le rapport de l'efficacité réelle par le rendement idéal de Carnot :

$r = \frac{\eta_{reel}}{\eta_{Carnot}}$

Par construction, à causes des pertes et des irréversibilités du système, le rendement r est toujours inférieur (dans le cas idéal, égal) à 1. Le rendement dépend des températures, mais aussi de la chimie des gaz utilisés, des frottements internes ou encore des pertes thermiques. Dans les cas réels, on approche la limite théorique de très loin : il reste beaucoup de progrès à faire dans ces domaines.

Exemples de machines thermiques

De nombreuses machines thermiques sont d'un usage courant, tels le moteur à explosion (un type de moteur à combustion interne, qui remplace la machine à vapeur...), le réfrigérateur, les pompes à chaleurs . Le moteur à combustion externe, pourtant prometteur, est peu courant.

Voir aussi

Articles connexes

• Sadi Carnot
• Rudolf Clausius
• Diagramme de Raveau

Ce document provient de « Machine thermique ».