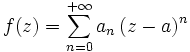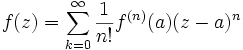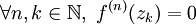- Principe des zéros isolés
-
Fonction analytique
Une fonction analytique est une fonction qui peut s'exprimer localement comme une série entière convergente. En analyse complexe, le résultat important est que les fonctions holomorphes sont analytiques.
Sommaire
Définition
Soit
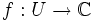 une fonction à variable complexe, où
une fonction à variable complexe, où 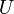 est un ouvert de
est un ouvert de 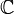 . On dit que la fonction
. On dit que la fonction 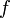 est analytique sur
est analytique sur 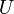 si pour tout
si pour tout 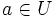 , il existe une suite
, il existe une suite 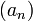 de nombres complexes et un réel
de nombres complexes et un réel 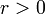 tel que, pour tout
tel que, pour tout 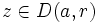 , c'est-à-dire pour tout
, c'est-à-dire pour tout 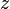 dans le disque (ouvert) de centre
dans le disque (ouvert) de centre 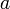 et de rayon
et de rayon  , supposé inclus dans
, supposé inclus dans 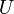 , on a :
, on a :Autrement dit, une fonction est analytique si elle est développable en série entière au voisinage de chaque point de son ensemble ouvert de définition.
Propriétés
- Une fonction analytique est holomorphe. Il existe d'ailleurs une réciproque à cette proposition, à savoir que toute fonction holomorphe sur un ouvert est analytique sur celui-ci.
- De plus, une fonction analytique est infiniment dérivable (au sens complexe, voir fonction holomorphe) et la dérivée n-ième en un point
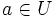 est
est 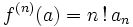 avec les notations données dans la définition. Ceci prouve que le développement de f en série entière au voisinage de chaque point a de U est unique ; on l'appelle encore développement en série de Taylor.
avec les notations données dans la définition. Ceci prouve que le développement de f en série entière au voisinage de chaque point a de U est unique ; on l'appelle encore développement en série de Taylor.
- L'ensemble des fonctions analytiques sur un ouvert est une algèbre: le produit par une constante d'une fonction analytique, la somme et le produit de fonctions analytiques sont analytiques.
- Lorsqu'elle est définie, la composée de fonctions analytiques est analytique.
- Toute série entière de rayon de convergence non nul définit sur son disque de convergence une fonction analytique. Ce n'est pas trivial, car une série entière est a priori un développement au voisinage d'un seul point.
- Toute fonction polynomiale est analytique sur
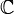 : on dit qu'elle est entière. Étant donnée une fonction polynomiale, les termes de son développement en série entière au voisinage d'un point quelconque de
: on dit qu'elle est entière. Étant donnée une fonction polynomiale, les termes de son développement en série entière au voisinage d'un point quelconque de 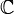 sont tous nuls à partir d'un certain rang d + 1 où d est le degré du polynôme. On obtient son développement en un point z0 à partir de son développement en un autre point à l'aide de la formule du binôme de Newton:
sont tous nuls à partir d'un certain rang d + 1 où d est le degré du polynôme. On obtient son développement en un point z0 à partir de son développement en un autre point à l'aide de la formule du binôme de Newton: 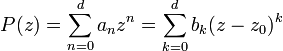 avec
avec 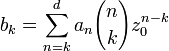 .
.
Exemples et contre-exemples
- La fonction exponentielle donnée par
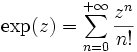 est analytique sur
est analytique sur 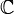 : c'est une fonction entière.
: c'est une fonction entière.
- La fonction
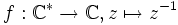 est analytique sur
est analytique sur 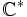 .
.
- La fonction
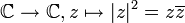 n'est pas analytique : on montre qu'elle n'admet de dérivée (au sens complexe) qu'en 0.
n'est pas analytique : on montre qu'elle n'admet de dérivée (au sens complexe) qu'en 0.
- La fonction
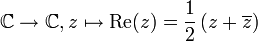 n'est pas analytique : elle n'admet de dérivée (au sens complexe) en aucun point de
n'est pas analytique : elle n'admet de dérivée (au sens complexe) en aucun point de 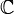 .
.
Les deux dernières fonctions admettent cependant des dérivées partielles de tous ordres (elles sont de classe
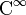 en tant que fonctions de deux variables réelles). Elles ne sont pas analytiques car l'ensemble des points où elles vérifient les équations de Cauchy-Riemann est d'intérieur vide (il est réduit à {0} pour la première, et vide pour la seconde).
en tant que fonctions de deux variables réelles). Elles ne sont pas analytiques car l'ensemble des points où elles vérifient les équations de Cauchy-Riemann est d'intérieur vide (il est réduit à {0} pour la première, et vide pour la seconde).Les principaux théorèmes
Le principe des zéros isolés
On considère maintenant un ouvert connexe
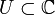 et une fonction analytique
et une fonction analytique 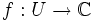 . Si
. Si 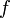 n'est pas la fonction nulle, alors tous ses zéros sont isolés, c'est-à-dire que si
n'est pas la fonction nulle, alors tous ses zéros sont isolés, c'est-à-dire que si 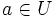 est tel que f(a) = 0, alors il existe un disque centré en
est tel que f(a) = 0, alors il existe un disque centré en 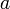 , inclus dans
, inclus dans 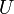 , tel que
, tel que 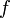 ne s'annule en aucun autre point que
ne s'annule en aucun autre point que 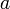 sur ce disque ; ceci se traduit par :
sur ce disque ; ceci se traduit par :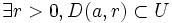 et
et 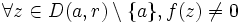
Ainsi, toute fonction
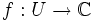 non constante (ie.
non constante (ie. 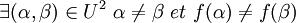 ), n'est constante en aucun point (ie. dans aucune direction à partir de ce point), ce qui se traduit par :
), n'est constante en aucun point (ie. dans aucune direction à partir de ce point), ce qui se traduit par :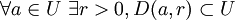 et
et 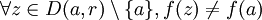
On en déduit qu'aucune fonction analytique
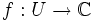 non constante ne peut avoir son image
non constante ne peut avoir son image 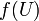 contenue dans un espace vectoriel réel de dimension 1 (en particulier,
contenue dans un espace vectoriel réel de dimension 1 (en particulier, 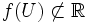 ). En effet, comme
). En effet, comme 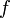 est continue car analytique, il devrait y avoir existence de courbes de niveau, et le résultat ci-dessus l'interdit, d'où ce dernier corollaire.
est continue car analytique, il devrait y avoir existence de courbes de niveau, et le résultat ci-dessus l'interdit, d'où ce dernier corollaire.Le principe du prolongement analytique
Article détaillé : prolongement analytique.Soient
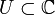 un ouvert, a un point de U et une fonction analytique
un ouvert, a un point de U et une fonction analytique 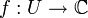 . On suppose en outre que U est connexe (cette hypothèse est essentielle). Alors les trois propositions suivantes sont équivalentes :
. On suppose en outre que U est connexe (cette hypothèse est essentielle). Alors les trois propositions suivantes sont équivalentes :- f est identiquement nulle sur U
- f est identiquement nulle dans un voisinage de a
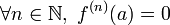
Ce théorème signifie que si une fonction analytique sur un ouvert connexe s'annule sur un disque de rayon si petit soit-il, alors c'est la fonction nulle. On peut interpréter cela comme un résultat d'unicité pour la théorie du prolongement analytique.
DémonstrationIl est clair que 1 implique 2 qui implique 3.
La fonction f est analytique sur U donc au voisinage de
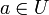 on a
on adonc si
on obtient bien que f est identiquement nulle au voisinage de a. Donc 3 implique 2.
Montrons maintenant que 2 implique 1. L'ensemble A des points de U telle que f soit nulle dans un voisinage de ces points est un ouvert par définition, et il est de plus non vide (on suppose 2). On prend maintenant une suite (zn) de points de A qui converge vers
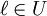 . Comme 2 implique 3, on a
. Comme 2 implique 3, on aLa fonction f étant analytique sur U, elle est développable en série entière en
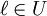 , et donc f est nulle au voisinage de
, et donc f est nulle au voisinage de 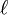 , donc
, donc 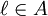 . Donc A est fermé dans U. Il est de plus non vide et ouvert dans U donc par connexité de U il vient A = U. Donc f est identiquement nulle sur U . Donc 2 implique 1.
. Donc A est fermé dans U. Il est de plus non vide et ouvert dans U donc par connexité de U il vient A = U. Donc f est identiquement nulle sur U . Donc 2 implique 1.Un corollaire de ce théorème nous dit que si deux fonctions analytiques coïncident sur un voisinage d'un point d'un ouvert connexe, alors ces deux fonctions sont égales.
Mathématiciens ayant travaillé sur le sujet
- De Moivre a établi la formule de Moivre.
- Stirling donna la formule de Stirling.
- Euler développa la théorie du logarithme et démontra qu'il existe une infinité de solutions complexes. Il est l'un des premiers à s'intéresser aux fonctions complexes.
- Legendre a développé la théorie des fonctions elliptiques.
- Gauss a démontré différents théorèmes se rapportant à l'analyse complexe.
- Laplace inventa la méthode d'estimation des intégrales qui porte son nom. Il a aussi introduit la transformée de Laplace.
- Poisson a fait, dans un article de 1813, le lien entre « étrangetés » en variable réelle et comportement de la fonction dans le plan complexe.
- Argand interpréta entre 1785 et 1830 les nombres complexes en terme géométrique.
- Cauchy a fourni plusieurs outils : théorème des résidus, intégrale curviligne, rayon de convergence...
- Riemann à qui l'on doit l'application conforme, la fonction zêta de Riemann...
- Weierstrass a étudié les singularités essentielles.
- Laurent a étudié le développement au voisinage d'un pôle.
- Émile Picard a publié deux théorèmes (le petit et le grand) sur les valeurs exceptionnelles
- Émile Borel a développé la théorie des séries divergentes, des transformations intégrales, de la croissance...
- Jacques Hadamard a fourni le théorème de décomposition, a démontré le théorème des nombres premiers...
- Landau
- Jensen a publié la formule de Jensen.
- Koebe
- Cahen s'est penché sur la théorie des séries de Dirichlet
- Paul Montel a publié sur les familles normales, le théorème de Montel...
- Valiron s'est intéressé à la théorie des fonctions entières ou méromorphes
- Blumenthal a publié la théorie des fonctions d'ordre infini.
Bibliographie
- Portail des mathématiques
Catégorie : Analyse complexe
Wikimedia Foundation. 2010.