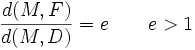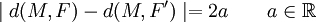- Hyperbole (mathematiques)
-
Hyperbole (mathématiques)
 Pour les articles homonymes, voir Hyperbole.
Pour les articles homonymes, voir Hyperbole.En mathématiques, une hyperbole est une figure géométrique de la famille des coniques caractérisée par une excentricité supérieure à 1.
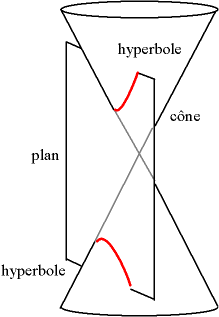
On obtient une hyperbole en prenant l'intersection d'un cône de révolution et d'un plan, le plan interceptant les deux branches du cône. Une hyperbole est constituée de deux branches disjointes. Bien que l'illustration ci-contre montre un plan vertical, tout angle plus faible que celui des génératrices du cône est acceptable.
Sommaire
Définition monofocale de l'hyperbole
Soient D une droite et F un point n'appartenant pas à D, et soit P le plan contenant la droite D et le point F. On appelle hyperbole de droite directrice D et de foyer F l'ensemble des points M du plan P vérifiant
où d(M,F) mesure la distance du point M au point F et d(M,D) mesure la distance du point M à la droite D.
La constante e est appelée excentricité de l'hyperbole.
Définition bifocale de l'hyperbole
L'hyperbole est lieu géométrique des points dont la différence des distances aux deux foyers est constante.
Géométriquement, cela donne :
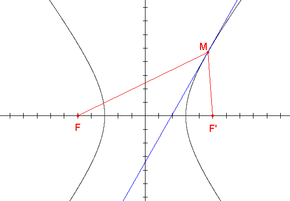
Soient F et F' deux points distincts du plan. On appelle hyperbole de foyers F et F' l'ensemble des points M du plan vérifiant la propriété suivante :
L'axe focal est le nom de la droite portant les deux foyers : c'est l'un des deux axes de symétrie de l'hyperbole, le seul qui la coupe. Pour cette raison, on le nomme aussi axe transverse et ses points communs avec la courbe sont les sommets. Le réel a de la définition ci-dessus apparaît comme la moitié de la distance entre les sommets.
En chaque point M de cette hyperbole, la bissectrice du secteur angulaire (FMF') se trouve être la tangente en M à la courbe.
Équations
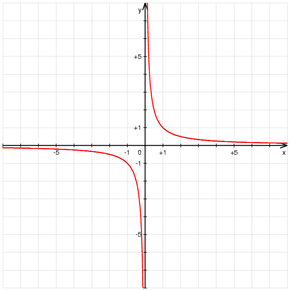
L'hyperbole dont l'expression mathématique la plus simple est la représentation graphique de la fonction f définie par f(x) = 1 / x, voir fonction inverse.
Cette hyperbole, ainsi que celles dont une équation cartésienne est de la forme x2 − y2 = a2 sont dites équilatères parce que leurs deux asymptotes sont orthogonales. Leur excentricité vaut
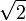 .
.Plus généralement, dans un repère dont les axes sont de symétrie pour l'hyperbole, l'axe transverse pour axe des abscisses, l'équation cartésienne se met sous la forme
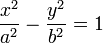
donnant alors les représentations paramétriques
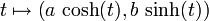 et
et 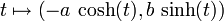
pour chacune des branches.
Matérialisation d'une hyperbole
- Lorsqu'une lampe munie d'un abat-jour est placée non loin d'un mur vertical, la courbe qui délimite, sur le mur, la zone éclairée et la zone ombragée est un arc d'hyperbole.
Liens externes
- http://www.mathcurve.com/courbes2d/hyperbole/hyperbole.shtml
- (en)Construire la géométrie analytique objets
Article connexe
- Portail de la géométrie
Catégorie : Conique
Wikimedia Foundation. 2010.