Groupe de galois

Groupe de Galois

Évariste Galois 1811-1832

En mathématiques, et plus spécifiquement en algèbre dans le cadre de la théorie de Galois, le groupe de Galois d'une extension de corps L sur un corps K est le groupe des automorphismes de corps de L laissant invariant K. le groupe de Galois est souvent noté Gal(L/K).

Si l'extension possède de bonnes propriétés, c’est-à-dire si elle est séparable et normale, on parle alors d'extension de Galois et les hypothèses du théorème fondamental de la théorie de Galois sont réunies. Il existe alors une bijection entre les sous-corps de L et les sous-groupes du groupe de Galois Gal(L/K).

La correspondance permet une compréhension profonde de la structure de l'extension. Un exemple important est le théorème d'Abel-Ruffini, il donne une condition nécessaire et suffisante de résolution par radicaux d'une équation algébrique.

Histoire

Genèse

Article détaillé : Théorème d'Abel-Ruffini#Histoire.

Niels Abel 1802-1829

Si l'histoire de la théorie des équations algébriques remonte à la nuit des temps, en revanche l'introduction du concept de groupe date du XVIIIe siècle. Joseph-Louis Lagrange (1736 1813) met en évidence la relation entre les propriétés des permutations des racines et la possibilité de résolution d'une équation cubique ou quartique^[1]. Paolo Ruffini (1765 1822) est le premier à comprendre que l'équation générale et particulièrement l'équation quintique n'admet pas de solution^[2]. Sa démonstration reste lacunaire. Les démonstrations de Niels Henrik Abel (1802 1829) dans deux articles écrits en 1824^[3] et 1826 passent, après des années d'incompréhension, à la postérité. Cependant la notion de groupe abstrait n'apparaît pas encore et le théorème reste incomplet.

Evariste Galois

Evariste Galois (1811 1832) résout définitivement la problématique en proposant une condition nécessaire et suffisante juste pour la résolvabilité de l'équation par radicaux. Son approche subit la même incompréhension que ses prédécesseurs. Ses premiers écrits, présentés à l'Académie des sciences dès 1829, sont définitivement perdus. Un article^[4] de l'auteur écrit en 1831 est découvert par Joseph Liouville (1809 1882) qui le présente à la communauté scientifique en 1843 en ces termes: "...J'espère intéresser l'Académie en lui annonçant que dans les papiers d'Évariste Galois j'ai trouvé une solution aussi exacte que profonde de ce beau problème : Étant donnée une équation irréductible décider si elle est ou non résoluble par radicaux.".

L'apport de Galois est majeur, G. Verriest^[5] le décrit dans les termes suivants : « le trait de génie de Galois c'est d'avoir découvert que le nœud du problème réside non pas dans la recherche directe des grandeurs à adjoindre, mais dans l'étude de la nature du groupe de l'équation. Ce groupe (...) exprime le degré d'indiscernabilité des racines (...). Ce n'est donc plus le degré d'une équation qui mesure la difficulté de la résoudre mais c'est la nature de son groupe. »

Galois modifie profondément son axe d'analyse par rapport à ses prédécesseurs. Pour la première fois dans l'histoire des mathématiques, il met en évidence une structure abstraite, qu'il appelle groupe de l'équation. C'est une étude sur la théorie des groupes abstraits qui lui permet de montrer qu'il existe des cas non résolubles. Il met ainsi en évidence que le groupe alterné d'ordre cinq ne possède pas les propriétés nécessaires pour être résoluble. Il écrit ainsi "Le plus petit nombre de permutations que puisse avoir un groupe indécomposable quand ce nombre n'est pas premier est 5.4.3."^[6]

Cette démarche, consistant à définir et analyser des structures abstraites et non plus des équations, est des plus fécondes. Elle préfigure ce qu'est devenue l'algèbre. Pour cette raison, Galois est souvent considéré comme un père de l'algèbre moderne.

L'évolution de la théorie

Deux mathématiciens comprennent immédiatement la portée du travail de Galois, Liouville et Augustin Louis Cauchy (1789 1855) qui publie dès 1845 un article démontrant le théorème sur les groupes finis portant son nom^[7]. Puis Arthur Cayley (1821 1895) donne une première définition abstraite de la structure de groupe^[8], indépendante de la notion de permutation. Camille Jordan (1838 1922) diffuse largement les idées de Galois. Son livre^[9] rend accessible la théorie à un public beaucoup plus vaste en 1870.

La théorie est petit à petit profondément modifiée par des mathématiciens comme Richard Dedekind (1831 1916) qui fut le premier à parler de théorie de Galois, Otto Hölder (1859 1937) qui démontra son théorème désormais célèbre en 1889 ou Emil Artin (1898 1962) qui donne la définition moderne d'un groupe de Galois^[10]. Le groupe de Galois est maintenant un groupe d'automorphismes et non un sous-groupe de permutations.

Motivation

Motivation originale

Article détaillé : Théorème d'Abel-Ruffini.

Initialement, le groupe de Galois est apparu comme un outil pour comprendre les équations algébriques. L'approche naïve consistant à opérer des changements de variables ou des transformations sur un polynôme ne permet pas de trouver algébriquement les racines.

Pour comprendre dans quel cas une telle démarche fonctionne, une bonne démarche consiste à étudier les permutations des racines qui laissent invariantes toutes les expressions algébriques de ces racines. Une telle structure forme un groupe, isomorphe au groupe de Galois.

La théorie de Galois permet alors de déterminer exactement dans quel cas il est possible d'exprimer les racines en fonctions d'expressions algébriques des coefficients de l'équation et de radicaux. Un radical est un nombre dont une puissance nième est un nombre du corps initial. La structure du groupe de Galois permet cette exacte détermination.

Une telle démarche, consistant à étudier non plus les transformations, mais la structure même de la plus petite extension contenant toutes les racines, appelée corps de décomposition, s'avère puissante. Elle est la base de l'algèbre moderne. Cette approche consiste à étudier de manière générale la structure d'un ensemble particulier, ici le corps de décomposition. Cet ensemble apparaît comme disposant d'une double structure, à la fois de corps et aussi d'espace vectoriel sur le corps des coefficients. Le groupe de Galois est la structure algébrique la plus simple permettant une compréhension profonde.

Les extensions finies

Article détaillé : Théorème fondamental de la théorie de Galois.

Cette approche générale est féconde pour l'analyse de toute extension finie sur n'importe quel corps de base. Cette analyse s'avère plus simple si l'extension possède de bonnes propriétés. Deux hypothèses sont utiles, l'extension doit être séparable et normale. On parle alors d'extension galoisienne. Il est néanmoins nécessaire de généraliser les concepts. Un groupe devient alors une structure abstraite qui s'éloigne de la notion de permutation. Le groupe de Galois n'est plus défini à l'aide des racines d'un polynôme car l'extension est maintenant définie de manière générale et non plus à partir d'une équation algébrique. Le groupe de Galois apparaît alors comme le groupe des automorphismes de l'extension laissant invariant le corps de base.

Le théorème fondamental de la théorie de Galois établit dans le cas d'une extension galoisienne une correspondance entre les sous-corps de l'extension et les éléments du groupe. Cette correspondance permet la compréhension fine de l'extension.

Le cas général

Le caractère fini de l'extension n'est pas nécessaire pour la définition du groupe de Galois. Dans le cas général, le groupe de Galois reste un outil fondamental. Cependant, la théorie devient suffisamment complexe pour être décomposée.

Le cas où le groupe de Galois est commutatif est maintenant parfaitement connu. La théorie des corps de classes correspond à la classification des extensions abéliennes. Cette théorie est considérée comme l'un des grands succès des mathématiques du XX^e siècle.

Le cas non commutatif est encore largement une question ouverte en mathématique. Le groupe de Galois reste un outil fondamental, comme le montrent par exemple les travaux de Laurent Lafforgue sur le programme de Langlands, qui lui valurent la médaille Fields en 2002.

Définition

Soit K un corps L une extension algébrique P(X) un polynôme à coefficients dans K, F un sous corps de L et Ω la clôture algébrique de K. Ces notations sont utilisées dans toute la suite de l'article, de plus L est identifiée à un sous-corps de Ω.

• On appelle groupe de Galois de l'extension L sur K le groupe des automorphismes de L laissant invariant K. Le groupe de Galois est souvent noté Gal (L/K).
• On appelle groupe de Galois du polynôme P[X] le groupe de Galois du corps de décomposition de P[X] sur K. Le groupe de Galois est alors souvent noté G_K(P[X]).

Exemples

Cas d'un polynôme de degré deux

Considérons un premier exemple, suffisamment simple pour que l'approche historique soit utilisable dans ce cas. Soit P[X] le polynôme à coefficient rationnel défini de la manière suivante:

$P[X]=X^2-2X-1\;$

Si l'on note x₁ et x₂ les deux racines de P[X], alors:

$x_1=1+\sqrt{2}\quad et \quad x_2=1-\sqrt{2}\;$

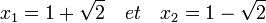
Considérons alors l'ensemble E des polynômes Q[X,Y] à deux variables tel que (x₁,x₂) soit racine. Les trois exemples de polynômes suivants vérifient cette propriété:

$Q_1[X,Y]=X^2-2X-1\quad Q_2[X,Y]=X+Y-2\; et\; Q_3[X,Y]=X.Y+1$

On remarque alors que (x₂,x₁) est aussi une racine d'un polynôme de cette nature. Ceci démontre que les deux permutations des racines, qui au couple (x₁,x₂) associent, l'une (x₁,x₂), et l'autre (x₂,x₁), laissent E stable.

Le groupe des deux permutations est isomorphe au groupe de Galois. Initialement c'est ainsi qu'il était défini. Il est ici isomorphe à Z/2Z. D'autres exemples sont donnés dans l'article Théorème d'Abel-Ruffini.

Applications

Si les groupes de Galois sont historiquement apparus à travers la théorie des équations algébriques, la puissance de ce concept a rapidement dépassé ce cadre.

Équations algébriques

Article détaillé : Équation algébrique.

Une équation algébrique est une équation qui s'écrit avec les quatre opérations +, -, . et /. Il est possible d'y ajouter les radicaux, c’est-à-dire des expressions correspondant à la racine nième d'un nombre. Toute équation de cette nature revient à une équation polynomiale. Si, dans les cas les plus fréquents, c’est-à-dire celui des réels ou complexes, la problématique de l'existence et du nombre de solutions est résolue, en revanche celui de la résolution explicite est restée longtemps une question ouverte. Certaines méthodes analytiques, comme celle de Newton par une suite convergente, ou celle d'Abel par des fonctions elliptiques apportent des solutions à cette question. Il reste néanmoins à trouver une méthode purement algébrique pour une telle question.

Dans les cas de polynômes de degré inférieur à cinq, cette question se résout par des changements de variables bien choisies. Dans le cas général une telle approche n'est pas satisfaisante. En effet, il n'existe pas de solution dans le cas général. Le groupe de Galois permet de fournir une condition nécessaire et suffisante, ainsi qu'une méthode explicite de résolution. Cette question est traitée par le théorème d'Abel.

Théorie des corps

Article détaillé : Théorie de Galois.

L'approche d'une équation algébrique par son groupe de Galois met en évidence la structure du corps K associé à l'équation. L'étude des corps est donc totalement liée à celle des groupes de Galois. C'est la raison pour laquelle la théorie des corps s'appelle la théorie de Galois.

Comme souvent en mathématiques, un outil puissant d'analyse de la structure de K consiste en l'étude de l'ensemble des sous-corps. Il en existe toujours un, celui engendré par l'unité pour la multiplication. Dans le cas ou K est de caractéristique nulle, alors le corps peut être considéré comme une extension des nombres rationnels. Dans le cas contraire, la caractéristique est égal à p, un nombre premier, et K peut être considéré comme une extension de Z/pZ. C'est la raison pour laquelle en théorie de Galois, il est peu question de sous-corps, mais essentiellement d'extensions. Un sous-corps est en effet considéré comme une extension du corps engendrée par l'unité et inclus dans le corps K.

Le théorème fondamental de la théorie de Galois indique qu'il existe une bijection entre le groupe de Galois et les extensions. C'est la raison pour laquelle les groupes de Galois sont un outil essentiel dans la théorie des corps.

Théorie algébrique des nombres

Article détaillé : Théorie algébrique des nombres.

En théorie des nombres, il existe une classification, nombres entiers, rationnels, constructibles, algébriques et transcendants. Un nombre est dit algébrique s'il est solution d'une équation algébrique. En conséquence, il est naturel que le groupe de Galois soit dans ce contexte un outil essentiel.

Un exemple est donné par les nombres constructibles. En termes de théorie de Galois, ces nombres apparaissent comme élément d'une tour d'extension quadratique. Le groupe de Galois associé à cette extension est abélien, ce qui permet de démontrer le théorème de Gauss-Wantzel et de trouver tous les polygones réguliers constructibles. Cette approche permet de même de démontrer de vieilles conjectures comme l'impossibilité dans le cas général de réaliser la trisection de l'angle ou la duplication du cube.

Article détaillé : Décomposition des idéaux premiers dans les extensions galoisiennes.

Par ailleurs, dans le cadre d'une extension galoisienne, la ramification admet en un certain sens une interprétation galoisienne : les groupes de ramifications, dont le groupe de décomposition et le groupe d'inertie, sont des sous-groupes du groupe de Galois, qui correspondent via la correspondance de Galois à des sous-extensions ayant des propriétés de décomposition maximale, ou de ramification minimale.

Une question importante est celle de l'étude du groupe de Galois absolu d'un corps, en particulier du corps des rationnels, c'est-à-dire du groupe de Galois de sa clôture séparable.

Géométrie algébrique

Article détaillé : Géométrie algébrique.

Enfin, en géométrie, une classe importante de variétés est constituée par les variétés algébriques. Ce sont les variétés définies comme une intersection d'un nombre fini de polynômes à plusieurs variables. L'analyse des corps associées à ces polynômes et donc des groupes de Galois est une voie essentielle pour la compréhension de ces géométries.

La correspondance de Galois qui à chaque extension associe un élément du groupe de Galois, devient alors une correspondance entre les éléments du groupe et des classes de revêtements d'une variété algébrique.

Voir aussi

Notes

1. ↑ Joseph-Louis Lagrange Réflexions sur la résolution algébrique des équations 1770
2. ↑ Paolo RuffiniLa théorie générale des équations dans laquelle il est démontré qu'il est impossible de donner les solutions générales des équations de degré strictement supérieur à 41799
3. ↑ Niels Henrik Abel Mémoire sur les équations algébriques, où l'on démontre l'impossibilité de la résolution de l'équation générale du cinquième degré 1824
4. ↑ Evariste Galois sur les conditions de résolubilité des équations algébriques 1846 Journal de Liouville
5. ↑ G. Verriest Œuvres Mathématiques d'Évariste Galois 1951 Gauthier-Villars, Paris
6. ↑ Evariste Galois Écrits et Mémoires Mathématiques d'Évariste Galois 1962 Gauthier-Villars, Paris
7. ↑ Augustin Louis Cauchy Sur le nombre de valeurs égale ou inégales que peut acquérir une fonction de n variables indépendantes, quand on permute ces variables entre elles d'une manière quelconque 1845
8. ↑ Arthur Cayley Sur la théorie des groupes comme dépendance de l'équation symbolique θⁿ = 1. 1854
9. ↑ Camille Jordan Traité des substitutions et des équations algébriques 1870
10. ↑ Emil Artin Théorie de Galois 1942 Notre Dame

Liens externes

• (fr) Mémoire sur les conditions de résolubilité des équations par radicaux (1830), texte de Galois et analyse sur le site BibNum.
• (en) Référence historiques de l'université de St Andrews
• (fr) Une courte présentation des extensions algébriques par Bernard le Stum Université de Rennes 1 2001
• (fr) Un cours de DEA sur la théorie de Galois par Alain Kraus Université de Paris VI 1998
• (fr) Groupe de Galois dans les-mathématiques.net
• (fr) Une approche naïve du groupe de Galois

Références

• R. et A. Douady, Algèbre et théories galoisiennes, Cedic/Fernand Nathan, 1978
• S. Lang, Algèbre, Dunod, 2004
• P. Samuel, Théorie algébrique des nombres, Hermann, Paris, 1971
• E. Galois, Écrits et Mémoires Mathématiques d'Évariste Galois, Gauthier-Villars, Paris, 1962
• G. Verriest, Œuvres Mathématiques d'Évariste Galois, Gauthier-Villars, Paris, 1951
• J.C. Carrega, Théorie des corps, Hermann, 1989
• E. Artin, Galois Theory, Notre Dame Press, Londres 1971

Ce document provient de « Groupe de Galois ».