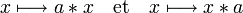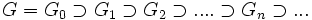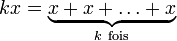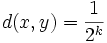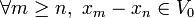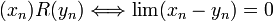Groupe Topologique

Groupe topologique

En mathématiques, on appelle groupe topologique tout groupe 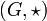$(G,\star)$ muni d'une topologie satisfaisant aux conditions suivantes:

• L'application 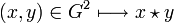$(x,y) \in G^2 \longmapsto x \star y$ est continue,
• L'application 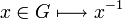$x\in G \longmapsto x^{-1}$ est continue.

Sur tout groupe topologique localement compact et séparable, il existe une et une seule mesure (à coefficient multiplicateur près) invariante par la translation à gauche 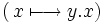$\left( \, x \longmapsto y.x \right)$ : la mesure de Haar.

Exemples de base

Le groupe additif 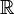$\mathbb{R}$. On peut montrer qu'un sous-groupe de 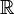$\mathbb{R}$ est soit dense, soit de la forme 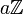$a\mathbb{Z}$, pour un unique $a\ge 0$.

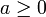Le cercle S¹, qui peut être considéré comme le groupe multiplicatif des nombres complexes de module 1 ou comme le groupe des rotations de centre fixé dans un plan euclidien. Tout sous-groupe S¹ est soit fini soit dense.

Un exemple plus sophistiqué est 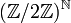$(\mathbb{Z}/2\mathbb{Z})^\mathbb{N}$. Ce groupe est homéomorphe à l'ensemble de Cantor. Pour le voir, on a besoin de la notion de produit infini d'espaces topologiques.

Quelques propriétés générales

Dans un groupe topologique, les translations

$x\longmapsto a*x\quad \mathrm{et} \quad x\longmapsto x*a$

sont des homéomorphismes.

La topologie est déterminée par la donnée des voisinages de l'élément neutre.

Un groupe topologique est séparé si et seulement si {e} est fermé dans G, ou, ce qui revient au même, si tout point est une partie fermée. La condition est évidemment nécessaire. Pour voir qu'elle est suffisante, notons qu'en raison de la continuité de la multiplication, pour tout ouvert U contenant l'élément neutre, il en existe un autre, que nous noterons V, tel que 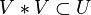$V*V\subset U$. Quitte à remplacer V par 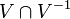$V\cap V^{-1}$, on peut supposer que V = V ^{− 1}. Si 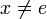$x\not=e$, on applique cette remarque à 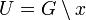$U=G\setminus x$. 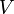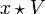Alors $V\,$ et $x\star V$ sont deux ouverts disjoints contenant e et x respectivement.

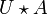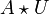Si U est une partie ouverte et A une partie quelconque, $U\star A$ et $A \star U$ sont ouverts, puisque, par exemple, $U\star A= \cup_{a\in A}U\star a$.

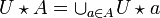Groupes linéaires

Dorénavant, nous omettrons le signe $\star$.

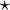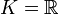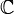Une classe importante de groupes topoloqiques est formée par les sous-groupes du groupe linéaire GL(n,K), avec $K=\mathbb{R}$ ou $\mathbb{C}$. On les munit de la topologie induite par celle de End(Kⁿ).

Ces exemples sont des exemples fondamentaux de groupes de Lie réels ou complexes. Ils ont en commun la propriété suivant : il existe un ouvert contenant l'élement neutre et ne contenant aucun sous-groupe non trivial.

Topologie p-adique

Si (G, + ) est un groupe abélien, si (G_n) est une suite de sous-groupes de G telle que:

$G = G_0\supset G_1 \supset G_2\supset ....\supset G_n \supset ...$

Alors la suite (G_n) induit une topologie sur G dans laquelle les voisinages de x sont les parties de G contenant un des ensembles x + G_n.

Si de plus, l'intersection des (G_n) est réduite à {0} où 0 est l'élément neutre de G, le groupe est séparé.

Un cas particulier de groupe topologique de cette forme est le groupe muni de la topologie p-adique: Si p est un entier naturel, la suite (G_n) est définie par G_n = pⁿG . (on rappelle que, pour tout entier naturel k et tout élément x de G, l'élément kx est défini par

$kx=\underbrace{x+x+\ldots+x}_{k\ \mathrm{fois}}$

Distance induite

On peut définir une distance sur (G, + ) muni de la topologie induite par (G_n) si l'intersection des G_n est bien réduite à $\{0\}~$:

$d(x,y)= \frac{1}{2^k}$

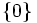où k est le premier entier tel que 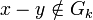$x-y \notin G_k$ et

d(x,y) = 0 si pour tout entier k, $x - y \in G_k$

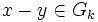
Complété

Si (G, + ) est un groupe abélien séparé muni de la topologie déterminée par la suite (G_n), on peut définir dans G des suites de Cauchy. Une suite (x_n) est de Cauchy si et seulement si, pour tout voisinage V₀ de 0, il existe un entier n tel que

$\forall m \geq n,\ x_m-x_n \in V_0$

Sur cet ensemble de suites de Cauchy noté S_C(G) on peut définir une relation d'équivalence:

$(x_n) R (y_n) \Longleftrightarrow \lim (x_n-y_n)=0$

L'ensemble quotient S_C(G) est alors un espace complet. Le groupe G est alors isomorphe à un sous-groupe dense de S_C(G).

L'exemple le plus important d'une telle construction est celui des nombres p-adiques : on fait cette construction à partir de 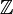$\mathbb{Z}\,$ et de la multiplication par un nombre premier $p\,$.

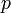Voir aussi

• R. Mneimné, F. Testard, Introduction à la théorie des groupes de Lie classiques, Hermann 1986, ISBN 2 7056 6040 2

• J. Lafontaine, Introduction aux variétés différentielles (ch. 4), ISBN 2 7061 0654 9

• R. Godement, Introduction à la théorie des groupes de Lie, (ch. 1 et 2), Springer 2004, IX, 305 p., Broché, ISBN 3-540-20034-7

Liens internes

• espace topologique
• groupes de Lie
• groupes profinis

Ce document provient de « Groupe topologique ».