Graphe de Hamming

Graphe de Hamming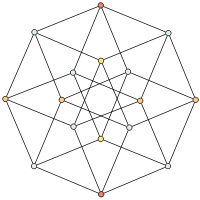
H(4,2)
Notation	H(d,q)
Nombre de sommets	qd
Nombre d'arêtes	${\frac {d\times(q-1)\times q^d}{2}}$
Distribution des degrés	d(q-1)-régulier
Diamètre	d
Utilisation	Code correcteur Parallélisation
modifier

Les graphes de Hamming forment une famille de graphes. Le graphe de Hamming de dimension d sur un alphabet de taille q est défini de la manière suivante : H(d,q) est le graphe dont les sommets sont S^d, l'ensemble des mots de longueur d sur un alphabet S, où | S | = q. Deux sommets sont adjacents dans H(d,q) s'ils sont à une distance de Hamming de 1, c'est-à-dire si leurs étiquettes ne diffèrent que d'un symbole^[1].

Construction

On peut construire le graphe de Hamming directement en appliquant sa définition : disposons q^d sommets, chacun avec une étiquette $(x_1,x_2,...,x_d), x_i \in \{0,1,2,...,q\}$. Deux sommets sont reliés par une arête si leurs étiquettes différent exactement d'un symbole, soit formellement pour le graphe G = (V,E) :

$\exists e_{uv} \in E \Leftrightarrow u = \{x_1, ..., x_{i-1}, x_i, x_{i+1}, ..., x_d\}, v = \{x_1, ..., x_{i-1}, x'_i, x_{i+1}, ..., x_d\}, x_i\neq x'_i$

On peut aussi définir H(d,q) comme le produit cartésien de d graphes complets K_q, soit :

$H(d,q) = H(d-1,q) \square K_q = H(d-2,q) \square K_q \square K_q = ... = \underbrace{K_q \square K_q \square ... \square K_q}_{n \text{ fois}}$

Propriétés

Fondamentales

• Degré. Deux sommets sont connectés s'ils diffèrent exactement sur un symbole de leurs étiquettes. Comme chaque étiquette a d symboles, chaque sommet est connecté à exactement d(q-1) voisins : tout sommet a donc degré d(q-1), autrement dit le graphe est d(q-1)-régulier.
• Nombre de sommets. Les sommets de H(d,q) sont étiquetés par l'ensemble des mots de longueur d sur un alphabet de cardinalité q. L'ordre de H(d,q) est donc égal à q^d.
• Diamètre. Le diamètre du graphe de Hamming H(d,q) est égal à d. En effet, une des propriétés du produit cartésien est que le diamètre D(C) de $C = A \square B$ est égal à D(A) + D(B). Comme H(d,q) est le produit cartésien de d graphes complets K_q, son diamètre est égal à $d \times D(K_q) = d \times 1 = d$.
• Distance régulier. Le graphe de Hamming est un graphe distance-régulier^[2].
• Eulérien. Un graphe a un chemin eulérien si et seulement si tout sommet est de degré pair. Comme H(d,q) est d(q-1)-régulier, il en résulte qu'il n'y a un chemin eulérien que pour d(q-1) pair.
• Cas particuliers :
  • Graphe complet. Par construction, H(1,q) est le graphe complet K_q.
  • Graphe trivial. Quel que soit d, H(d,1) est le graphe trivial à un sommet.
  • Hypercube. L'hypercube Q_d est isomorphe par construction avec le graphe de Hamming H(d,2).

Aspects algébriques

Graphe de Cayley

Le graphe de Hamming H(d,q) est un graphe de Cayley Cay(G, S) avec :

$G = \underbrace{{\frac { \mathbb Z} {q \mathbb Z}} \times {\frac { \mathbb Z} {q \mathbb Z}} \times ... \times {\frac { \mathbb Z} {q \mathbb Z}}}_{d\text{ fois}}$ $S=\{(i,0,0,...,0),(0,i,0,...,0),...,(0,0,...,i,0),(0,0,...,0,i)| 1 \leq i \leq q\}$

C'est un des exemples de référence en théorie algébrique des graphes^[3].

Symétrie

Le graphe de Hamming est symétrique. Cela signifie que son groupe d'automorphisme agit transitivement sur l'ensemble de ses sommets et sur l'ensemble de ses arêtes. En d'autres termes, tous les sommets et toutes les arêtes d'un graphe de Hamming jouent exactement le même rôle d'un point de vue d'isomorphisme de graphe.

La symétrie se démontre en deux points : l'arête-transitivité et la sommet-transitivité. La sommet-transitivité découle directement du fait que le graphe de Hamming est un graphe de Cayley. Par construction, tous les graphes de Cayley sont sommet-transitifs^[4].

Une démonstration alternative s'appuie sur le fait que le graphe de Hamming est un produit cartésien de graphes complets, donc de graphes sommets-transitifs. Un théorème statue que le produit de deux graphes sommets-transitifs est sommet-transitif ^[5].

L'arête-transitivité peut se démontrer en constatant que le graphe de Hamming est un G-graphe^[6].

Références

1. ↑ (en) Andries E. Brouwer - Brouwer home page Hamming Graphs].
2. ↑ (en) Brouwer, A. E.; Cohen, A. M.; and Neumaier, A. "Hamming Graphs." §9.2 in Distance-Regular Graphs. New York: Springer-Verlag, pp. 261-267, 1989.
3. ↑ (en) Cai Heng Li - on-line Cayley graph in Encyclopaedia of Mathematics, Springer, (ISBN 1402006098).
4. ↑ (en) Pegg, Ed Jr.; Rowland, Todd; and Weisstein, Eric W - Cayley Graph, wolfram.com.
5. ↑ (en) Wilfried Imrich & Sandi Klavžar, Product Graphs: Structure and Recognition. Wiley, 2000, (ISBN 0-471-37039-8)
6. ↑ (en) Alain Bretto, Cerasela Jaulin, Luc Gillibert, Bernard Laget: "A New Property of Hamming Graphs and Mesh of d-ary Trees". ASCM 2007: 139-150