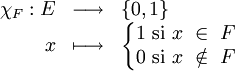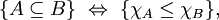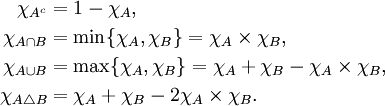Fonction caractéristique d'un ensembel

Fonction caractéristique (théorie des ensembles)

Pour les articles homonymes, voir Fonction caractéristique.

Le graphe de la fonction indicatrice d'un sous-ensemble à deux dimensions d'un carré.

En mathématiques, une fonction caractéristique, ou fonction indicatrice, est une fonction définie sur un ensemble E qui explicite l’appartenance ou non à un sous-ensemble F de E de tout élément de E.

Formellement, la fonction caractéristique d’un sous-ensemble F d’un ensemble E est une fonction :

$\begin{array}{rcl} \chi_F : E & \longrightarrow & \{0,1\} \\ x & \longmapsto & \left\{\begin{matrix} 1 \ \mbox{si} \ x \ \in \ F \\ 0 \ \mbox{si} \ x \ \notin \ F \end{matrix}\right. \end{array}$

La fonction caractéristique de F est souvent notée χ_F ou 1_F.

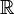Par exemple, la fonction de Dirichlet est la fonction caractéristique de $\mathbb{Q}$ dans $\mathbb{R}$ : elle est définie sur 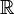$\mathbb{R}$ et vaut 1 si x est rationnel, 0 sinon. Comme 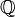$\mathbb{Q}$ est dense dans 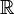$\mathbb{R}$, c'est une fonction partout discontinue.

Attention

Le terme de fonction indicatrice est parfois utilisé pour fonction caractéristique. Cette dénomination a également pour avantage d'éviter la confusion avec la fonction caractéristique utilisée en probabilité.

La fonction 1_F peut désigner la fonction identité.

Propriétés

Si A et B sont deux sous-ensembles de E alors

$\{A \subseteq B\}\ \Leftrightarrow\ \{\chi_{A} \le \chi_{B}\},$

et

$\begin{align} \chi_{A^c} &= 1 - \chi_A, \\ \chi_{A\cap B} &= \min\{\chi_A,\chi_B\} = \chi_A \times \chi_B, \\ \chi_{A\cup B} &= \max\{{\chi_A,\chi_B}\} = \chi_A + \chi_B - \chi_A \times \chi_B, \\ \chi_{A \triangle B} &= \chi_A + \chi_B - 2 \chi_A \times \chi_B. \end{align}$

Voir aussi

• Analyse
• Mesure
• Fonction simple (combinaison linéaire de fonctions indicatrices)
• Fonction étagée (fonction simple mesurable)

Références

• Folland, G.B.; Real Analysis: Modern Techniques and Their Applications, 2nd ed, John Wiley & Sons, Inc., 1999.
• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Section 5.2: Indicator random variables, pp.94–99.
• Martin Davis ed. (1965), The Undecidable, Raven Press Books, Ltd., New York.
• Stephen Kleene, (1952), Introduction to Metamathematics, Wolters-Noordhoff Publishing and North Holland Publishing Company, Netherlands, Sixth Reprint with corrections 1971.
• George Boolos, John P. Burgess, Richard C. Jeffrey (2002), Cambridge University Press, Cambridge UK, ISBN 0-521-00758-5.
• Lotfi A. Zadeh, 1965, "Fuzzy sets". Information and Control 8: 338–353. [1]
• Joseph Goguen, 1967, "L-fuzzy sets". Journal of Mathematical Analysis and Applications 18: 145–174

Ce document provient de « Fonction caract%C3%A9ristique (th%C3%A9orie des ensembles) ».