- Fer À Cheval De Smale
-
Fer à cheval de Smale
L'application fer à cheval est un des exemples classiques de systèmes dynamiques. Elle fut introduite par Stephen Smale à l'occasion de l'étude de l'oscillateur de Van der Pol. Son comportement est chaotique alors qu'on l'obtient en effectuant une succession d'opérations géométriques très simples : rétrécissement dans une direction, étalement dans une autre, et repliement en forme de fer à cheval.
L'application fer à cheval est un difféomorphisme qui laisse stable la figure formée d'un carré avec deux demi-disques accolés. Certains des points du carré initial ont leur image rejetée à l'extérieur de ce carré, ils n'y retourneront alors jamais. Finalement peu de points restent définitivement dans le carré ; ils forment un ensemble fractal et appartiennent à l'espace invariant de l'application. Les points rejetés à l'extérieur convergent, eux, vers un point fixe, situé dans un des demi-disques.
Les propriétés essentielles de cette dynamique sont :
- l'existence d'une infinité d'orbites périodiques ;
- parmi elles, on peut en trouver ayant des périodes arbitrairement longues ;
- le nombre de telles orbites augmente exponentiellement avec la période ;
- au voisinage de tout point de l'espace invariant il existe un point périodique.
Description de la transformation
La transformation fer à cheval a quelques ressemblances avec la transformation du boulanger, et de fait ces deux transformations sont topologiquement équivalentes. Cependant l'application fer à cheval est plus compliquée à décrire, car elle constitue un difféomorphisme et laisse une certaine région S du plan invariante (S étant formée du carré avec ses demi-disques).
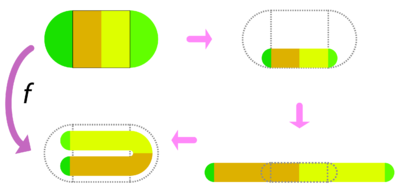
On définit f par composition, en appliquant d'abord une affinité orthogonale de rapport a < 1 / 2 selon l'axe vertical aux points du carré, tandis que les demi-disques subissent une homothétie pour garder leur forme de disque. Il est important que le facteur a soit strictement inférieur à 1/2 pour assurer une marge entre les deux branches du fer à cheval dans la dernière étape. On applique ensuite au rectangle une affinité orthogonale dans l'autre direction, et de rapport 1 / a, sans changer les demi-disques. Au terme de ces deux étapes l'aire du carré a été conservée, pas celle des demi-disques.
Enfin vient la phase de repliement : la bande obtenue peut être repliée et replacée dans S, avec la partie courbée qui sort du carré initial, elle se trouve dans un demi-disque initial, les petits demi-disques se trouvant dans l'autre.
Voir aussi
Références
- S. Smale : Differentiable dynamical systems. In: Bulletin of the American Mathematical Society. 73/1967, S. 747-817
- P. Cvitanović, G. Gunaratne et I. Procaccia : Topological and metric properties of Hénon-type strange attractors. In: Physical Review A. 38/1988, S. 1503-1520
- A. de Carvalho : Pruning fronts and the formation of horseshoes. In: Ergodic theory and dynamical systems. 19/1999, S. 851-894
- A. de Carvalho et T. Hall : How to prune a horseshoe. In: Nonlinearity. 15/2002, S. R19-R68
- Portail des mathématiques
Catégorie : Système dynamique remarquable
Wikimedia Foundation. 2010.