- Espace pseudometrique
-
Espace pseudométrique
En mathématiques, un espace pseudométrique est un cas particulier d'espace hémimétrique vérifiant une relation de symétrie, qui généralise ainsi la notion d'espace métrique. Lorsqu'une topologie est générée par une famille de pseudométriques, l'espace est appelé espace de jauge.
Les pseudométriques apparaissent naturellement en analyse fonctionnelle.
Sommaire
Définition
Un espace pseudométrique
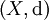 est la donnée d'un ensemble X et d'une fonction positive à valeurs réelles
est la donnée d'un ensemble X et d'une fonction positive à valeurs réelles 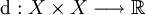 , appelée fonction pseudométrique (ou pseudométrique), qui vérifie les trois relations suivantes :
, appelée fonction pseudométrique (ou pseudométrique), qui vérifie les trois relations suivantes :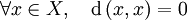 ;
;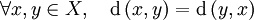 (symétrie) ;
(symétrie) ;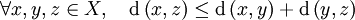 (inégalité triangulaire).
(inégalité triangulaire).
À la différence d'un espace métrique, les points d'un espace pseudométrique ne sont pas nécessairement distincts — c'est-à-dire que l'on peut avoir d(x,y) = 0 pour des valeurs distinctes
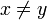 .
.Exemples
Soit l'espace
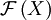 des fonctions à valeurs réelles
des fonctions à valeurs réelles 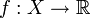 , ajouté du point
, ajouté du point 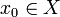 . Ce point induit une pseudométrique sur l'espace des fonctions, donnée par :
. Ce point induit une pseudométrique sur l'espace des fonctions, donnée par :
Pour un espace vectoriel V, une seminorme p induit une pseudométrique[1] sur V :Propriétés topologiques
La topologie pseudométrique est induite par l'ensemble des boules ouvertes :
qui forme une base de la topologie.[2] Un espace topologique est dit pseudométrisable si on peut munir l'espace d'une topologie pseudométrique.
Identification métrique
L'annulation de la pseudométrique induit une relation d'équivalence, appelée identification métrique, qui fait de l'espace pseudométrique un espace métrique complet. Cela peut être fait en définissant x˜y si
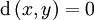 . Soit X * = X / ˜ et posons :
. Soit X * = X / ˜ et posons :Alors d * est une métrique sur X * et
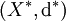 est un espace métrique bien défini.
est un espace métrique bien défini.L'identification métrique préserve les topologies induites : un sous-ensemble
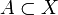 est ouvert (resp. fermé) de
est ouvert (resp. fermé) de 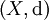 si et seulement si
si et seulement si ![\pi\left(A\right)=\left[A\right]](/pictures/frwiki/55/7019454aa9b83e455ed247e4c1653f42.png) est un ouvert (resp. fermé) de
est un ouvert (resp. fermé) de 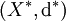 .
.Références
- ↑ Réciproquement, une pseudométrique invariante par translation et homogène induit une seminorme.
- ↑ (en) PlanetMath : Pseudometric topology.
- (en) Cet article est partiellement ou en totalité issu d’une traduction de l’article de Wikipédia en anglais intitulé « Pseudometric space ».
Bibliographie
- (en) L.A. Steen, J.A.Seebach Jr. : Counterexamples in topology, (1970) Holt, Rinehart and Winston, Inc.
- (en)/(ru) A.V. Arkhangelskii, L.S.Pontryagin : General Topology I, (1990) Springer-Verlag, Berlin. ISBN 3-540-18178-4
- Portail des mathématiques
Catégories : Espace métrique | Topologie
Wikimedia Foundation. 2010.

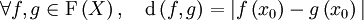
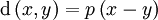
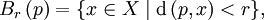
![\mathrm d^{*} \left( \left[x\right],\left[y\right] \right) = \mathrm d\left(x,y\right)](/pictures/frwiki/48/07c0fe5ee7c8018527bf03a72715d212.png)