- Espace Fonctionnel
-
Espace fonctionnel
En mathématiques, un espace fonctionnel est un ensemble d'applications d'une certaine forme d'un ensemble X vers un ensembleY. Il est appelé espace parce que suivant les cas il peut être un espace topologique ou un espace vectoriel ou les deux. Les espaces fonctionnels apparaissent dans différents domaines des mathématiques:
- En théorie des ensembles, l'ensemble des parties d'un ensemble X peut être identifié avec l'ensemble des fonctions de X à valeurs dans {0,1}; noté {0,1}X. Plus généralement, l'ensemble des applications
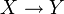 est noté YX;
est noté YX;
- en algèbre linéaire l'ensemble des applications linéaires d'un espace vectoriel E vers un autre F sur un même corps commutatif est lui-même un espace vectoriel;
- En analyse fonctionnelle, on peut aussi rencontrer des espaces fonctionnels avec les applications linéaires continues, munis de topologies, et les exemples principaux sont les espaces de fonctions numériques muni d'une topologie; les exemples les plus connus sont les espaces hilbertiens et les espaces de Banach.
- en analyse fonctionnelle, l'ensemble des applications de l'ensemble des entiers naturels dans un ensemble quelconque X est appelé espace séquentiel. Il est formé de l'ensemble des suites d'éléments de X;
- en topologie, on peut essayer de construire une topologie sur l'espace des fonctions continues d'un espace topologique X dans un autre Y, dont l'utilité dépend de la nature des espaces. Une topologie couramment employée est celle de compact-ouvert. Un autre topologie possible est la topologie produit sur l'espace des fonctions (pas nécessairement continues) YX. Dans ce contexte, cette topologie est aussi désignée sous le nom de topologie de la convergence simple;
- En topologie algébrique, l'étude de la théorie de l'homotopie repose essentiellement sur l'étude des invariants discrets des espaces de fonctions;
- dans la théorie des processus stochastiques, le problème technique de base est comment construire une mesure de probabilité sur un espace de fonctions constitué de chemins de processus (fonctions du temps);
- dans la théorie des catégories un espace fonctionnel est appelé un objet exponentiel. Il apparaît d'une certaine façon comme la représentation du bifoncteur canonique; mais en tant que foncteur (simple), du type [X, -], il apparaît comme foncteur adjoint à un foncteur de type (-×X) sur des objets ;
- en lambda-calcul et en programmation fonctionnelle, des types d'espaces de fonctions sont employés pour exprimer l'idée de fonction d'ordre supérieur;
- dans la théorie des domaines, l'idée fondamentale est de trouver des constructions à partir d'ordres partiels qui peuvent modéliser le lambda-calcul, en créant une catégorie cartésienne fermée.
Sommaire
Liste d'espaces fonctionnels
Analyse fonctionnelle
Espaces généraux
- Les espaces localement convexes: des espaces vectoriels avec une famille de semi-normes (ou de façon équivalente possédant une base locale d'ensembles convexes).
- les espaces de Fréchet: un espace vectoriel avec une famille dénombrable de semi-normes (ou de façon équivalente pourvu d'une distance invariante par translation).
- les espaces de Banach: des espaces vectoriels avec une famille finie de semi-normes (ou de façon équivalente avec une simple norme).
- les espaces de Hilbert: des espaces vectoriels munis de produit scalaire.
Espaces particuliers
- Espace de Schwartz des fonctions indéfiniment dérivables à convergence rapide et son espace dual, des distributions tempérées;
- espace Lp
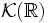 espace des fonctions continues à support compact muni de la norme de la convergence uniforme;
espace des fonctions continues à support compact muni de la norme de la convergence uniforme;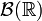 espace des fonctions continues bornées (fonction bornée);
espace des fonctions continues bornées (fonction bornée);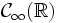 ensemble des fonctions qui tendent vers zéro à l'infini;
ensemble des fonctions qui tendent vers zéro à l'infini;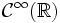 espace des fonctions indéfiniment dérivables;
espace des fonctions indéfiniment dérivables;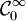 espace des fonctions indéfiniment dérivables à support compact muni de la norme uniforme (et de celle avec ses dérivées);
espace des fonctions indéfiniment dérivables à support compact muni de la norme uniforme (et de celle avec ses dérivées);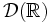 espace des fonctions à support compact muni de la topologie limite inductive;
espace des fonctions à support compact muni de la topologie limite inductive;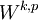 espace de Sobolev;
espace de Sobolev; espace des fonctions holomorphes;
espace des fonctions holomorphes;- Application linéaires;
- applications linéaires par morceaux;
- espace des fonctions continues muni de la topologie compact-ouvert;
- espace des fonctions muni de la topologie de la convergence simple;
- Espaces de Hardy
- Espace de Hölder
Voir aussi
- Portail des mathématiques
Catégorie : Espace vectoriel topologique - En théorie des ensembles, l'ensemble des parties d'un ensemble X peut être identifié avec l'ensemble des fonctions de X à valeurs dans {0,1}; noté {0,1}X. Plus généralement, l'ensemble des applications
Wikimedia Foundation. 2010.
