Espace Dodécaédrique De Poincaré

Espace dodécaédrique de Poincaré

L'espace dodécaédrique de Poincaré en dimension 2 correspond à une sphère pavée de douze pentagones sphériques réguliers. Chaque fois que l'on sort par une face de couleur, on rentre par la face opposée (de même couleur) après avoir tourné la sphère de 36°.

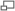
L'espace dodécaédrique de Poincaré (en anglais Poincaré dodecahedral space) est un espace topologique multiconnexe ayant pour revêtement la sphère. En dimension 2, on peut se le représenter comme un pavage régulier de la sphère « usuelle » à l'aide de pentagones (il y a en tout douze pentagones pour couvrir la sphère entière), chaque pentagone étant identifié à son homologue antipodal (la face opposée) moyennant une rotation de π / 5, c'est-à-dire 36°, de façon à ce que les faces se correspondent. Comprendre par là que, quand on sort par une face, on rentre par son opposée, mais en ayant tourné de 36° (en examinant la photographie ci-contre, on voit bien que les deux faces vertes, qui sont antipodales, ne sont pas « tournées » de la même façon, si bien qu'elles ne sont pas superposables sans la rotation additionnelle). Cet espace est donc fini, mais sans bord.

Formellement, l'espace dodécaédrique de Poincaré peut se définir comme le quotient de son revêtement (la sphère S) par le groupe d'isométries laissant invariant l'icosaèdre élémentaire, ce dernier étant lui même engendré par deux générateurs. Ce groupe d'isométries est isomorphe au groupe SL(2, 5) des matrices carrées d'ordre 2 à coefficients dans le corps fini Z/5Z dont le déterminant est égal à 1.

Intérêt cosmologique

L'espace dodécaédrique de Poincaré est un des candidats potentiels à la forme globale de l'univers. C'est du moins ce que pense une équipe d'astrophysiciens emmenés par Jean-Pierre Luminet, de l'observatoire de Paris-Meudon.

Si cette hypothèse est correcte, le fond cosmologique diffus (CMB) devrait posséder des motifs sphériques. Ces motifs sont liés au fait que, dans un espace multiconnexe, la lumière peut emprunter plusieurs trajets pour arriver au même point, en passant par les faces opposées (qui sont identifiées). Par exemple, dans un espace torique tridimensionnel, homologue à un cube dont on identifierait les faces opposées, un observateur se voit trois fois (une fois en face, une fois de côté, une fois en haut). Le fond cosmologique devrait donc présenter ces sortes de figures d'interférence. Cependant, à l'heure actuelle, même si les données du satellite WMAP semblent compatibles avec l'hypothèse de l'espace dodécaédrique de Poincaré, la recherche des cercles n'a pas été concluante — pour autant que ces cercles puissent effectivement être détectés malgré le bruit de fond et d'autres effets perturbateurs ^[1].

Références

1. ↑ (en) S. Caillerie, M. Lachièze-Rey, J.-P. Luminet, R. Lehoucq, A. Riazuelo, J. Weeks , A new analysis of Poincaré dodecahedral space model, arXiv:0705.0217 voir en ligne

Ce document provient de « Espace dod%C3%A9ca%C3%A9drique de Poincar%C3%A9 ».