- Equation du temps
-
Équation du temps
Sommaire
L’équation du temps est un paramètre utilisé en astronomie pour rendre compte du mouvement apparent relatif du soleil par rapport au soleil moyen, lesquels peuvent différer l'un par rapport à l'autre de plus ou moins un quart d'heure environ. D'une année sur l'autre, la courbe d'évolution annuelle de ce paramètre se répète quasiment à l'identique. La connaissance de l'équation du temps donne le moyen de corriger à tout instant l'heure donnée par un cadran solaire pour trouver l'heure légale (d'écoulement uniforme). Autrefois, elle permettait de corriger l'heure donnée par une horloge (à écoulement théoriquement uniforme) pour trouver l'heure donnée par un cadran solaire (donc pour déterminer notamment le midi vrai, alors important socialement).
L'équation du temps peut se calculer très précisément. On en trouve des tables détaillées dans les éphémérides astronomiques[1].
Remarque sur le mot « équation » : en astronomie ancienne, le terme « équation » désignait une correction ajoutée algébriquement à une valeur moyenne pour obtenir une valeur vraie. C'est une telle acception qui a survécu dans l'expression « équation du temps ». Il s'agit bien d'un paramètre, et non d'une équation au sens habituel du terme (égalité avec inconnues, comme c'est le cas d'une équation polynomiale ou d'une équation différentielle).
Définition
L’équation du temps, à un instant donné, est la différence entre le temps solaire moyen et le temps solaire vrai[2],[3].
- Le temps solaire moyen est basé sur le soleil moyen, défini comme un objet qui, tout au long de l'année, se déplacerait sur l'équateur à une vitesse constante, telle que la durée du jour solaire moyen soit de 24 heures exactement.
- Le temps solaire ou temps vrai est une mesure du temps basée sur le soleil vrai, tel que donné par un cadran solaire. En particulier, le midi solaire correspond à l'instant de la journée où le soleil atteint son point le plus élevé dans le ciel.
Une valeur positive de l'équation du temps indique que le soleil est en retard sur le soleil moyen (c'est-à-dire plus à l'est), et une négative qu'il est en avance (c'est-à-dire plus à l'ouest). Par exemple, lorsque l'équation du temps vaut + 8 minutes, cela signifie qu'il est 12 h 08 du temps solaire moyen lorsque le cadran solaire indique midi vrai[4]. C'est du moins la convention de signe utilisée en France, où l’équation du temps est l'équation du temps vrai, c'est-à-dire ce qu'il faut ajouter au temps vrai pour obtenir le temps moyen. Dans certains pays, tels que le Royaume-Uni, les États-Unis ou la Belgique, l'équation du temps est définie avec la convention de signe inverse : c'est l'équation du temps moyen, c'est-à-dire la quantité qu'il faut ajouter au temps moyen pour obtenir le temps vrai. Les deux variables, « équation du temps vrai » et « équation du temps moyen » ont des valeurs opposées.
Autre forme de la définition : l’équation du temps, à chaque instant, est la différence entre l'ascension droite du soleil moyen et celle du soleil vrai.
Allure de l'évolution de l'équation du temps
Analemme
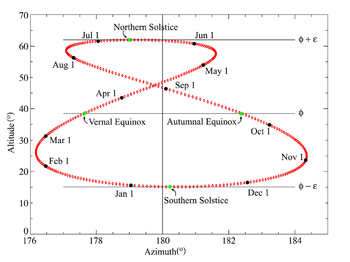
L'allure de l'évolution annuelle de l'équation du temps, en un lieu donné, peut être visualisée à l'aide d'une courbe appelée analemme ou courbe en 8, définie comme suit : chaque point de cette courbe représente une position du soleil (vrai) lorsqu'il est 12 h pour le soleil moyen, c'est-à-dire lorsque ce dernier passe au centre du diagramme. Les axes sont les suivants, avec des échelles différentes, de façon à mieux mettre en évidence la légère asymétrie de la courbe :
- L'axe horizontal représente l'azimut en degrés (180° correspond au sud). L'équation du temps se lit le long de cet axe, donc comme l'écart horizontal par rapport à la ligne 180°. Avec la convention de signe adoptée, elle est positive à gauche de la ligne 180°. La correspondance entre l'angle et le temps est 360° = 24 h, donc 1° = 4 minutes.
- L'axe vertical représente la hauteur du soleil au-dessus de l'horizon.
- Le soleil moyen (à midi moyen) se trouve au centre du diagramme (azimut = 180°, hauteur = 90° - latitude du lieu)
Sur l'exemple ci-contre[6], le premier jour de chaque mois est affiché en noir, et les positions des solstices et équinoxes sont affichées en vert. On lit par exemple :
- le 3 novembre, avance maximale du soleil vrai sur le soleil moyen, et l'équation du temps, qui est négative, vaut - 16 min 23 sec ;
- le 12 février, le retard est maximal, et l'équation du temps, qui est positive, vaut + 14 min 20 sec ;
- au solstice d'hiver, vers le 21 décembre, la hauteur du soleil est minimale et vaut 15,08° (hauteur au solstice d'hiver = colatitude du lieu - obliquité de l'écliptique = 38,52° - 23,44°) ;
- au solstice d'été, vers le 21 juin, la hauteur est maximale et vaut 61,96° (hauteur au solstice d'été = colatitude du lieu + obliquité de l'écliptique = 38,52° + 23,44°) ;
- aux équinoxes, le soleil passe dans le plan de l'équateur et a, à ce moment-là, la même hauteur que le soleil moyen, égale à la colatitude du lieu
Certains cadrans solaires sont munis d'un analemme. Ils peuvent même donner directement le temps moyen, soit parce que les droites horaires sont transformées en courbes corrigées de l'équation du temps, soit parce que le gnomon a reçu une forme tenant compte de cette correction. Dans les deux cas, il faut tenir compte de la période de l'année ou disposer de deux cadrans.
Allure de l'équation du temps comme fonction du temps
Allure actuelle
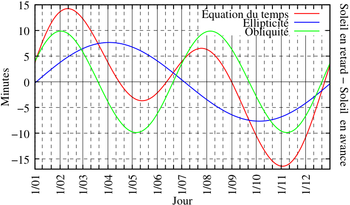
L'évolution de l’équation du temps sur une année complète est représentée par la courbe rouge sur la figure ci-contre. En première approximation, sa forme s'analyse comme résultant de la superposition de deux sinusoïdes :
- En bleu sur le diagramme : une sinusoïde de période égale à un an, d'amplitude égale à 7,66° et s'annulant aux apsides (au périgée le 3 janvier et à l'apogée début juillet). Comme on le verra plus loin, cette composante est due à l'excentricité de l'orbite.
- En vert sur le diagramme, une sinusoïde de période égale à une demi-année, d'amplitude 9,87° et s'annulant aux solstices et aux équinoxes. Comme on le verra plus loin, cette composante est un effet de l'obliquité de l'écliptique sur l'équateur.
L'équation du temps, en rouge, s'annule quatre fois par an, vers le 15 avril, le 13 juin, le 1er septembre et le 25 décembre. Son maximum, atteint vers le 11 février, vaut 14 min 15 s, et son minimum, atteint vers le 3 novembre, vaut − 16 min 25 s.
Évolution de l'allure
La forme de la courbe « équation du temps », c'est-à-dire la valeur des extrema et les instants où on les observe, ainsi que les instants où la courbe s'annule, évoluent très lentement au cours des années pour au moins deux raisons :
- la Terre dans son mouvement autour du Soleil subit l'influence des autres planètes du système solaire, ce qui entraîne une variation de l'excentricité de son orbite,
- la Terre dans sa rotation sur elle-même subit l'influence du couple (Lune, Soleil), ce qui entraîne une variation de son obliquité en inclinaison et direction; ces phénomènes sont connus et décrits sous le nom de nutation en longitude, nutation en obliquité et précession des équinoxes.
Ces évolutions provoquent notamment un glissement relatif des dates des apsides par rapport à celles des solstices et des équinoxes, qui sont fixes par construction de l'année tropique. Sur une durée de 70 siècles, de l'an - 2000 à + 5000, les extrema sont définis par le tableau suivant[7] :
Année Premier maximum Premier minimum Deuxième maximum Deuxième minimum - 2000 + 18 min 33 s, 31 janvier - 12 min 45 s, 20 mai + 2 min 06 s, 10 août - 9 min 30 s, 26 octobre - 1000 + 18 min 18 s, 3 février - 10 min 14 s, 21 mai + 2 min 06 s, 6 août - 11 min 45 s, 27 octobre 0 + 17 min 27 s, 6 février - 7 min 44 s, 20 mai + 2 min 57 s, 1er août - 13 min 45 s, 29 octobre + 1000 + 16 min 04 s, 9 février - 5 min 27 s, 18 mai + 4 min 30 s, 29 juillet - 15 min 20 s, 1er novembre + 2000 + 14 min 15 s, 11 février - 3 min 41 s, 14 mai + 6 min 30 s, 26 juillet - 16 min 25 s, 3 novembre + 3000 + 12 min 08 s, 14 février - 2 min 37 s, 10 mai + 8 min 41 s, 25 juillet - 16 min 57 s, 6 novembre + 4000 + 9 min 52 s, 15 février - 2 min 24 s, 6 mai + 10 min 48 s, 25 juillet - 16 min 54 s, 9 novembre + 5000 + 7 min 38 s, 15 février - 3 min 00 s, 3 mai + 12 min 38 s, 26 juillet - 16 min 17 s, 12 novembre Analyse intuitive de l'équation du temps
Influence de l'ellipticité de l'orbite de la terre
Les étapes du retour du midi vrai[4] d'un jour à l'autre, c'est à dire le retour d'un méridien donné face au soleil, peuvent se décomposer comme suit :
- une rotation complète (360°) de la terre sur elle-même pour passer de 1 à 2,
- ce faisant la terre a avancé sur son orbite autour du soleil, et de ce fait elle montre ce même méridien non pas face au soleil mais face aux étoiles lointaines, point 2,
- une rotation complémentaire de la terre sur elle-même est alors nécessaire pour que le méridien soit à nouveau face au soleil, point 3; cette rotation complémentaire est proportionnelle à la vitesse de la Terre le long de son orbite, si la vitesse est variable alors l'angle complémentaire de rotation est variable.
La seconde loi de Kepler (loi des aires) indique que la vitesse de la Terre varie le long de cette orbite;

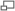
-
- elle s'accroit depuis son aphélie pour devenir maximale (30,287 km/s) à son périhélie (aux alentours du 3 janvier),
- puis ensuite décroit pour devenir minimale (29,291 km/s) à son aphélie (une demi-année plus tard);
- l'accélération est maximale à mi-chemin (aux alentours de début avril) entre l'aphélie et le périhélie,
- la décélération est maximale à mi-chemin (aux alentours de début octobre) entre le périhélie et l'aphélie,
- accélération et décélération sont nulles en ces deux points (périhélie et l'aphélie),
- pendant la phase d'accélération, la rotation complémentaire est donc à chaque fois plus importante pour compenser l'avance plus importante sur l'orbite, ce qui entraine un retard à chaque fois plus important du retour du midi vrai[4],
- et inversement pendant la phase de décélération,
- le retard est maximal lorsque l'accélération est maximale; il est minimal lorsque la décélération est maximale.
En première approximation, ce retard varie sinusoïdalement avec une période d'une année, s'annule au périhélie et à l'aphélie, et est extrémal entre ces deux points (courbe bleue de la figure équation du temps). L'expression de ce retard, exprimé en minutes, du à l'ellipticité est le suivant:
ΔTC(d) = 7,53.cos(B) + 1,5.sin(B) = 7,678.sin(B + 1,374) Voir la définition de B(d) ci-dessous.
Influence de l'obliquité de la terre
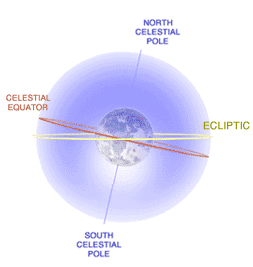 Ce schéma montre le plan de l'écliptique et celui de l'équateur céleste qui interceptent chacun un grand cercle sur une sphère virtuelle appelée sphère céleste.
Ce schéma montre le plan de l'écliptique et celui de l'équateur céleste qui interceptent chacun un grand cercle sur une sphère virtuelle appelée sphère céleste.
L'intersection de ces 2 plans définit l'axe vernal.
L'angle entre ces 2 plans est appelé l'obliquité.Même si l'orbite de la terre était circulaire, le mouvement apparent du soleil le long de l'équateur céleste ne serait pas uniforme. C'est une conséquence de l'inclinaison de l'axe de rotation de la terre par rapport à son plan orbital.
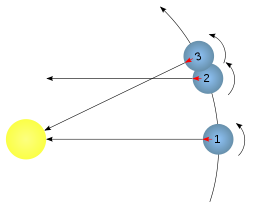
L'introduction du paragraphe précédent décompose en 3 étapes le retour d'un méridien donné face au soleil; la figure ci-contre montre ces mêmes 3 étapes mais en adoptant un point de vue géocentrique, c'est à dire la terre est fixe au centre de la figure et le soleil orbite autour de la terre:
- une rotation complète (360°) de la terre sur elle-même pour passer de 1 à 2,
- ce faisant le soleil a avancé sur son orbite autour de la terre, et de ce fait la terre montre ce même méridien non pas face au soleil mais face aux étoiles lointaines, point 2,
- une rotation complémentaire de la terre sur elle-même est alors nécessaire pour que le méridien soit à nouveau face au soleil, point 3
Le soleil a avancé de façon régulière sur son orbite située dans le plan écliptique, alors que la rotation complémentaire de la terre sur elle-même pour se remettre face au soleil est mesurée dans le plan de l'équateur céleste. Il faut donc rapporter le mouvement du soleil dans ce plan de l'équateur céleste pour apprécier le retard ou l'avance du temps solaire par rapport à une horloge régulière. C'est cette opération, appelée réduction à l’équateur, qui explique que le mouvement apparent du soleil le long de l'équateur céleste n'est pas uniforme.
Comme indiqué en début de ce paragraphe, supposons une orbite circulaire. Le module du vecteur vitesse du soleil est donc constant le long de son orbite. Les 2 composantes de ce vecteur sont l'une portée par l'axe vernal, l'autre portée par un vecteur orthogonal à cet axe vernal et situé dans le plan écliptique. La première composante se projette sans modification sur le plan de l'équateur céleste, la seconde se projette avec un facteur de réduction égal au cosinus de l'obliquité. De façon intuitive, la somme de ces 2 projections sur le plan de l'équateur céleste sera minimale sur l'axe vernal et maximale sur la quadrature de ce même axe. La variation de vitesse sera donc nulle en ces 4 points, et de même pour l'avance ou le retard.
En première approximation, il s'agit d'une sinusoïde de période une demi-année (courbe verte de la figure équation du temps) qui s'annule 4 fois sur une année, en particulier à l'équinoxe de printemps. L'expression de ce retard, exprimé en minutes, du à l'obliquité est le suivant:
ΔTR(d) = − 9,87.sin(2B) Voir la définition de B(d) ci-dessous.
Version simplifiée de l'équation temps
La somme des 2 formules précédentes fournit une première approximation de l'équation du temps :
ΔT(d) = ΔTC(d) + ΔTR(d) C'est à dire:
ΔT(d) = 7,678.sin(B + 1,374) − 9,87sin(2B) avec:
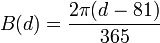 , exprimé en radians, dépend du numéro du jour de l'année : d = 1 le 1er janvier ; d = 81 à l'équinoxe de printemps.
, exprimé en radians, dépend du numéro du jour de l'année : d = 1 le 1er janvier ; d = 81 à l'équinoxe de printemps.Étude détaillée
Influence de l'ellipticité de l'orbite de la terre
- Calcul de l'anomalie moyenne
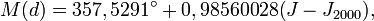
avec J2000 = 2451545. J est le jour julien de la date considérée. En première approximation, (J − J2000) peut être remplacé par le numéro d du jour dans l'année (d = 1 le premier janvier).
- Contribution de l'ellipticité de la trajectoire : c'est l'équation du centre en radian
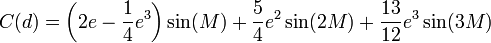
Application numérique :
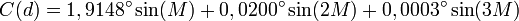
Influence de l'obliquité de la terre
- Calcul de la longitude écliptique
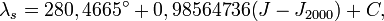
la petite différence de période entre λs et M est est due à la précession des équinoxes
- Contribution de l'obliquité de la Terre : c'est la réduction à l'équateur (en radian)
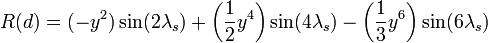
Application numérique :
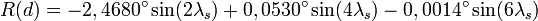
Équation du temps
Équation du temps en degrés:
E(d) = C(d) + R(d), où C et R sont exprimés en degrés. Équation du temps en minutes:
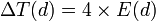 , où E est exprimé en degrés.
, où E est exprimé en degrés.Explications et démonstration de la formule
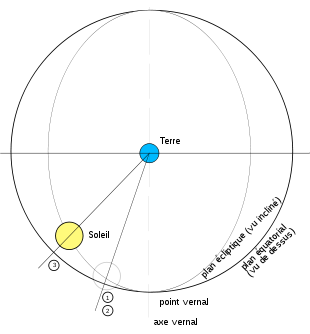
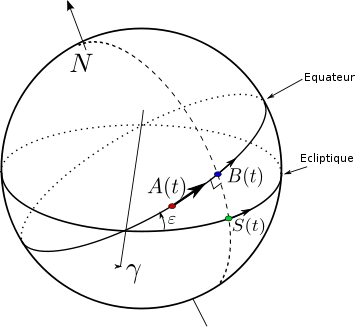
La figure 1 montre la Terre T qui tourne sur elle même et qui tourne autour du Soleil S en un an dans le plan de l'écliptique. La situation présentée correspond à l'automne. Le point P est le périhélie atteint au début du mois de janvier. L'angle θ s'appelle anomalie vraie. L'axe γ appelé axe vernal ou point vernal est l'intersection du plan de l'écliptique avec le plan équatorial. Il sert d'origine pour mesurer la longitude écliptique λs.
La figure 2 représente la Terre dans un repère fixe par rapport aux étoiles. L'obliquité
 est l'angle entre le plan de l'écliptique et le plan de l'équateur.
est l'angle entre le plan de l'écliptique et le plan de l'équateur.Appellons t le temps qui s'écoule. Considérons un point
 fixé sur Terre et positionné sur l'équateur. Il fait donc un tour en un jour sidéral de façon régulière.
fixé sur Terre et positionné sur l'équateur. Il fait donc un tour en un jour sidéral de façon régulière.Partant du centre de la terre, le point
 est situé en direction du Soleil. Il se situe donc sur le cercle de l'écliptique. Le point
est situé en direction du Soleil. Il se situe donc sur le cercle de l'écliptique. Le point 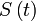 fait un tour en une année sidérale.
fait un tour en une année sidérale.Comme l'orbite terrestre est elliptique et d'après les lois de Kepler,
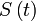 ne tourne pas de façon régulière. Considérons le méridien passant par
ne tourne pas de façon régulière. Considérons le méridien passant par 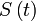 et appelons
et appelons 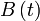 l'intersection de ce méridien avec l'équateur. Remarquons qu'il est midi solaire au point A lorsque le point
l'intersection de ce méridien avec l'équateur. Remarquons qu'il est midi solaire au point A lorsque le point 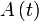 traverse ce méridien (i.e. lorsque les points
traverse ce méridien (i.e. lorsque les points 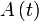 et
et 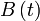 coïncident). Remarquons aussi qu'un jour solaire
coïncident). Remarquons aussi qu'un jour solairevrai est la durée qui sépare deux croisements de
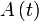 et
et 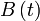 . Plus généralement l'heure solaire vraie est l'angle entre
. Plus généralement l'heure solaire vraie est l'angle entre 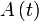 et
et 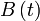 :
: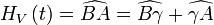
HV est l'heure qu'indiquerait un cadran solaire.
Pour définir l'heure solaire moyenne, il faut se référer à des mouvements réguliers (moyennés). Nous avons vu que le point
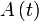 a un mouvement régulier. Ce n'est pas le cas du point
a un mouvement régulier. Ce n'est pas le cas du point 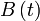 , ni même du point
, ni même du point 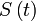 . A la place de
. A la place de 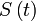 on considère un point virtuel
on considère un point virtuel 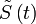 sur l'écliptique qui a un mouvement régulier et de même période (on verra que
sur l'écliptique qui a un mouvement régulier et de même période (on verra que 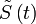 est directement relié à l'anomalie moyenne
est directement relié à l'anomalie moyenne 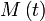 ).
).Par conséquent l'heure solaire moyenne est:
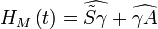
Par définition l'équation du temps est la différence:
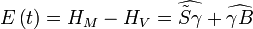
Or une relation de trigonométrie donne:
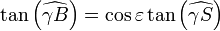
En effet, projetons à partir du centre de la terre le triangle sphérique SγB sur le plan tangent à la terre au point vernal γ. Il devient un triangle rectangle d'angle
 au sommet γ et de côté adjacent
au sommet γ et de côté adjacent  et d'hypothénuse
et d'hypothénuse  . On déduit la relation
. On déduit la relation 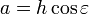 .
.On déduit:
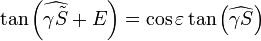
et l'expression de l'équation du temps:

Remarques
- Dans cette dernière équation tout est connu. D'une part, d'après la figure 1 il apparaît que l'angle
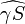 est reliée à la longitude écliptique λs par
est reliée à la longitude écliptique λs par
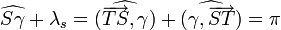
et λs elle même est reliée à l'anomalie vraie
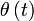 par
par 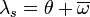 où
où 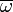 est la longitude du périhélie. Donc
est la longitude du périhélie. Donc
De même
 est relié à l'anomalie moyenne
est relié à l'anomalie moyenne  par
par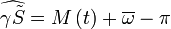
- Traditionnellement on décompose E(t) de la façon suivante:
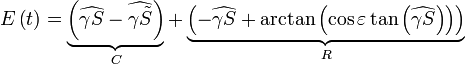
Le premier terme C appelé "contribution de l'ellipticité" ou équation du centre
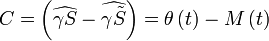 est dû à l'ellipticité de l'orbite terrestre. Dans un modèle où la Terre aurait un mouvement circulaire et régulier, on aurait
est dû à l'ellipticité de l'orbite terrestre. Dans un modèle où la Terre aurait un mouvement circulaire et régulier, on aurait 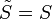 et seul le deuxième terme R appelé réduction à l'équateur dû à l'obliquité
et seul le deuxième terme R appelé réduction à l'équateur dû à l'obliquité  interviendrait. Remarquer que si
interviendrait. Remarquer que si 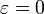 (le soleil en permanence dans le plan de l'équateur) ce dernier terme serait nul.
(le soleil en permanence dans le plan de l'équateur) ce dernier terme serait nul.- À l'aide d'un développement limité et posant
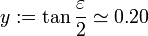 le terme réduction à l'équateur ci-dessus peut s'écrire
le terme réduction à l'équateur ci-dessus peut s'écrire
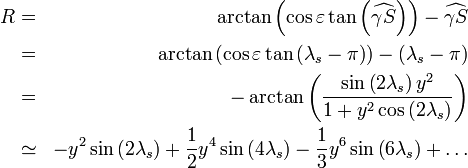
Notes et références
- ↑ Dans les Éphémérides Astronomiques publiées par la Société astronomique de France, la valeur de l'équation du temps est donnée, pour chaque jour de l'année à 0 h de Temps universel.
- ↑ Voir définition donnée par l'« Institut de mécanique céleste et de calcul des éphémérides » (Observatoire de Paris - Bureau des longitudes - CNRS) Temps vrai, temps moyen, équation du temps.
- ↑ Voir définition donnée par Laplace dans son livre Exposition du système du monde - Livre Premier, chapitre 3, fin du §3.
- ↑ a , b et c midi vrai est l'heure où le soleil est le plus haut dans le ciel (culmination) et où l'ombre d'un objet est donc la plus courte :
- cette ombre indique précisément le nord (dans l'hémisphère nord) ou le sud (dans l'hémisphère sud) ;
- quel que soit le jour de l'année, il est midi vrai exactement au même moment pour tous les points situés sur un même méridien ;
- il ne faut pas confondre le temps solaire vrai avec la durée d'ensoleillement qui varie en fonction de la latitude et de la saison.
- ↑ Schéma établi en utilisant les données de hauteur et d'azimut fournies par le site JPL Horizons
- ↑ Un diagramme similaire se trouve sur le site [1]
- ↑ Source : Meeus et Savoie.
Voir aussi
Articles connexes
Liens externes
- (fr) Les échelles de temps par l'Institut de mécanique céleste et de calcul des éphémérides
- (fr) L'équation du temps de Kepler
- (en) Article très complet sur l'équation du temps
Bibliographie
- Pierre-Simon Laplace, Exposition du système du monde
- Jean Meeus et Denis Savoie, L’Équation du temps, in revue l'Astronomie, vol. 109, juin 1995, p. 188-193.
- Portail de l’astronomie
Catégories : Mécanique céleste | Cadran solaire
Wikimedia Foundation. 2010.