Endomorphisme lineaire
- Endomorphisme lineaire
-
Endomorphisme linéaire
En mathématiques, un endomorphisme linéaire ou endomorphisme d'espace vectoriel ou endomorphisme est une application linéaire d'un espace vectoriel E dans lui-même.
L'ensemble des endomorphismes d'un espace vectoriel E est habituellement noté End(E) ou 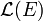 .
.
Rappelons que l'ensemble 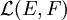 des applications linéaires d'un K-espace-vectoriel dans un autre est un espace est un K-espace vectoriel muni de la loi d'addition des fonctions et de la multiplication externe par un scalaire de K. Ainsi
des applications linéaires d'un K-espace-vectoriel dans un autre est un espace est un K-espace vectoriel muni de la loi d'addition des fonctions et de la multiplication externe par un scalaire de K. Ainsi 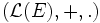 est une K-espace vectoriel.
est une K-espace vectoriel.
Propriétés des endomorphismes
Nous ne rappellerons pas ici toutes les propriétés des applications linéaires et qui sont donc aussi vérifiées par les endomorphismes linéaires.
Avec les lois d'espace vectoriel + et ., et plus la loi de composition des applications,  est une algèbre non commutative.
est une algèbre non commutative.
Signalons la formule du binôme qui est vérifiée lorsque deux endomorphismes commutent.
à compléter ...
Les endomorphismes en dimension finie
Lorsque l'espace vectoriel est de dimension finie, l'étude d'un endomorphisme se ramène immédiatement à celle de sa matrice par rapport à une base donnée. Souvent la même base de E est considérée au départ qu'à l'arrivée. La matrice obtenue est une matrice carrée.
Diagonalisation des endomorphismes
Endomorphismes en dimension finie
En dimension finie, la diagonalisation d'un endomorphisme consiste à trouver une base dans laquelle la matrice de l'endomorphisme s'écrit sous une forme diagonale. De manière générale, tous les endormorphismes ne sont pas diagonalisables, il est possible dans certains cas tout au plus de les trigonaliser. L'intérêt de la diagonalisation est de pouvoir étudier facilement un endomorphisme, de calculer aisément ses puissances nèmes, de rechercher ses racines carrées etc.
Endomorphismes quelconques
Voir aussi
Catégorie : Application linéaire
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Endomorphisme lineaire de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Endomorphisme Linéaire — En mathématiques, un endomorphisme linéaire ou endomorphisme d espace vectoriel ou endomorphisme est une application linéaire d un espace vectoriel E dans lui même. L ensemble des endomorphismes d un espace vectoriel E est habituellement noté… … Wikipédia en Français
Endomorphisme linéaire — En mathématiques, un endomorphisme linéaire ou endomorphisme d espace vectoriel est une application linéaire d un espace vectoriel dans lui même. L ensemble des endomorphismes d un espace vectoriel E est habituellement noté End(E) ou . L ensemble … Wikipédia en Français
Endomorphisme Nilpotent — Exemple d image d une base par un endomorphisme nilpotent en dimension 3. Un endomorphisme nilpotent est un morphisme d un objet mathématique sur lui même, qui, composé par lui même un nombre suffisant de fois, donne l application nulle. Un… … Wikipédia en Français
Endomorphisme nilpotent — Exemple d image d une base par un endomorphisme nilpotent en dimension 3. Un endomorphisme nilpotent est un morphisme d un objet mathématique sur lui même, qui, composé par lui même un nombre suffisant de fois, donne le morphisme nul. C’est donc… … Wikipédia en Français
Endomorphisme Autoadjoint — En mathématiques et plus précisément en algèbre linéaire, un endomorphisme autoadjoint est un cas particulier d application linéaire. Cette propriété s applique à une application linéaire d un espace vectoriel dans lui même ; pour cette… … Wikipédia en Français
Endomorphisme auto-adjoint — Endomorphisme autoadjoint En mathématiques et plus précisément en algèbre linéaire, un endomorphisme autoadjoint est un cas particulier d application linéaire. Cette propriété s applique à une application linéaire d un espace vectoriel dans lui… … Wikipédia en Français
LINÉAIRE ET MULTILINÉAIRE (ALGÈBRE) — LINЙAIRE ET MULTILINЙAIRE (ALGИBRE) L’algèbre linéaire sur un corps commutatif, telle qu’on la trouvera présentée ici, s’est progressivement dégagée, au cours du XIXe siècle et au début du XXe, de la théorie des équations linéaires (systèmes de n … Encyclopédie Universelle
Endomorphisme autoadjoint — En mathématiques et plus précisément en algèbre linéaire, un endomorphisme autoadjoint ou opérateur hermitien est un endomorphisme d espace de Hilbert qui est son propre adjoint (sur un espace de Hilbert réel on dit aussi endomorphisme… … Wikipédia en Français
Endomorphisme — En mathématiques, un endomorphisme est un morphisme (ou un homomorphisme) d un objet mathématique sur lui même. Ainsi, par exemple, un endomorphisme d espace vectoriel E est une application linéaire f : E → E et un endomorphisme de groupe G… … Wikipédia en Français
Endomorphisme de Weingarten — Application de Gauss En géométrie différentielle classique, l application de Gauss est une application naturelle différentiable sur une surface de R3, à valeurs dans la sphère unité S2, et dont la différentielle permet d accéder à la seconde… … Wikipédia en Français
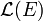 .
.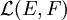 des applications linéaires d'un K-espace-vectoriel dans un autre est un espace est un K-espace vectoriel muni de la loi d'addition des fonctions et de la multiplication externe par un scalaire de K. Ainsi
des applications linéaires d'un K-espace-vectoriel dans un autre est un espace est un K-espace vectoriel muni de la loi d'addition des fonctions et de la multiplication externe par un scalaire de K. Ainsi 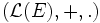 est une K-espace vectoriel.
est une K-espace vectoriel.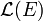 est une algèbre non commutative.
est une algèbre non commutative.
