Endomorphisme Normal
- Endomorphisme Normal
-
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Endomorphisme Normal de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Endomorphisme normal — Un endomorphisme normal est un opérateur d un espace de Hilbert qui commute avec son adjoint. Sommaire 1 Définition 2 Exemples 3 Propriétés 4 Article connexe … Wikipédia en Français
Endomorphisme Autoadjoint — En mathématiques et plus précisément en algèbre linéaire, un endomorphisme autoadjoint est un cas particulier d application linéaire. Cette propriété s applique à une application linéaire d un espace vectoriel dans lui même ; pour cette… … Wikipédia en Français
Endomorphisme auto-adjoint — Endomorphisme autoadjoint En mathématiques et plus précisément en algèbre linéaire, un endomorphisme autoadjoint est un cas particulier d application linéaire. Cette propriété s applique à une application linéaire d un espace vectoriel dans lui… … Wikipédia en Français
Endomorphisme autoadjoint — En mathématiques et plus précisément en algèbre linéaire, un endomorphisme autoadjoint ou opérateur hermitien est un endomorphisme d espace de Hilbert qui est son propre adjoint (sur un espace de Hilbert réel on dit aussi endomorphisme… … Wikipédia en Français
Normal — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Normal », sur le Wiktionnaire (dictionnaire universel) Le mot normal (au féminin normale) est un… … Wikipédia en Français
Opérateur normal — Endomorphisme normal Définition Soit un espace préhilbertien, réel ou complexe. Soit un endomorphisme de admettant un adjoint . On dit que est normal si … Wikipédia en Français
Endomorphisme de Weingarten — Application de Gauss En géométrie différentielle classique, l application de Gauss est une application naturelle différentiable sur une surface de R3, à valeurs dans la sphère unité S2, et dont la différentielle permet d accéder à la seconde… … Wikipédia en Français
Reduction d'endomorphisme — Réduction d endomorphisme En mathématiques, et plus particulièrement en algèbre linéaire, la réduction d endomorphisme est une technique mathématique qui a pour objectif d exprimer des matrices et des endomorphismes sous une forme plus simple,… … Wikipédia en Français
Réduction d'endomorphisme — En mathématiques, et plus particulièrement en algèbre linéaire, la réduction d endomorphisme est une technique mathématique qui a pour objectif d exprimer des matrices et des endomorphismes sous une forme plus simple, notamment pour faciliter les … Wikipédia en Français
Espace Stable Par Un Endomorphisme — En algèbre linéaire, un endomorphisme laisse stable un sous espace vectoriel F quand les éléments de F ont pour image un élément de F. La recherche de sous espaces stables est étroitement liée à la théorie de la réduction des endomorphismes. L… … Wikipédia en Français
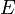 un espace préhilbertien, réel ou complexe. Soit
un espace préhilbertien, réel ou complexe. Soit 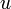 un endomorphisme de
un endomorphisme de 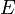 admettant un adjoint
admettant un adjoint 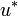 . On dit que
. On dit que 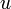 est normal si
est normal si 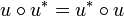 .
.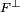 sont à la fois u-stables et u * -stables.
sont à la fois u-stables et u * -stables.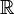 ou
ou 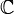 espace vectoriel muni d'une norme
espace vectoriel muni d'une norme 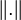 alors
alors 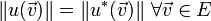 .
.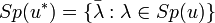 , où
, où 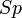 est le spectre de l'application.
est le spectre de l'application.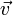 est un vecteur propre de u associé à une valeur propre λ, alors il est un vecteur propre de u * pour la valeur propre
est un vecteur propre de u associé à une valeur propre λ, alors il est un vecteur propre de u * pour la valeur propre 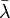 .
.