- Ellipsoide de revolution
-
Ellipsoïde de révolution
Une ellipsoïde de révolution est un modèle géométrique couramment utilisé pour approximer une géoïde. Chaque système géodésique (repère dans lequel sont calculées les coordonnées GPS par exemple) dépend d'une ellipsoïde de révolution. Elle permet de calculer une coordonnée appelée hauteur géodésique (souvent notée he) qui est la distance entre un point et la surface de ladite ellipsoïde.
Sommaire
Paramétrisation d'une ellipsoïde de révolution
Une paramétrisation possible d'une ellipsoïde de révolution est :
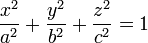
Définition
z'Oz axe de révolution de l'ellipsoïde a demi grand axe b demi petit axe Autres définitions
D'autres valeurs permettant de caractériser une ellipsoïde de révolution sont également utilisées[1] :
f (pour flattening) aplatissement 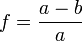
première excentricité e 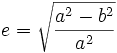
deuxième excentricité e' 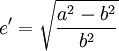
On distingue alors deux types d'ellipsoïdes de révolution :
b > a l'ellipsoïde est en forme de ballon de rugby ou cigare (prolate en anglais) b < a l'ellipsoïde est du type galette (oblate en anglais). Ellipsoïdes de révolution par type
Type galette
La figure méridienne est donc une ellipse ordinaire d'excentricité e = c/a avec a² - b² = c².
Pour une colatitude θ :
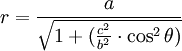
Attention à la différence entre : normale en M et radiale OM.
Le volume est V = 4/3. Pi. a².b . La surface est S = 2.Pi.a² +2.Pi.b² . 1/2e .[Ln(1+e)-Ln(1-e)]
Un système de coordonnées convenant bien à l'étude est :
- x = a cosh v . sinθ.cosφ
- y = a cosh v . sinθ.sinφ
- z = a sinh v . cosθ
Cas particulier d'ellipsoïde de révolution : IAG GRS 80
Voici, à titre d'exemple , les valeurs des paramètres de l'ellipsoïde de révolution IAG GRS 80, associée au système géodésique WGS84 utilisé par le GPS [1] :
Par définition :
demi grand axe a = 6 378 137,0 m aplatissement f = 1/298,257 222 101 Par calcul :
demi petit axe b 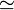 6 356 752,314 140 355 847 852 106 m
6 356 752,314 140 355 847 852 106 mpremière excentricité e 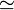 0,081 819 191 32
0,081 819 191 32Circonférence équatoriale 2.π.a 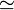 40 075,017 km (2.π.b
40 075,017 km (2.π.b 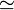 39 940,652 km)
39 940,652 km)Longueur de l'ellipse méridienne (par intégrale elliptique) : 40 007,863 km, ce qui prouve que la réalisation du mètre-étalon en platine iridié n'a pas été trop mal faite (précision 2×10-5) au XVIIIe siècle.
À titre indicatif :
- la surface est : S = 510,065 622 millions de km2 ( un moyen mnémotechnique : S ≈ (2.π.R)²/π ; et aussi : on peut environ coller 1000 fois la France sur le globe terrestre).
- le volume est : 1083 milliards de km3 avec une densité moyenne de 5,5, soit une masse de 6×1024kg.
Type cigare
La formule donnant le volume est la même.
La formule donnant la surface est différente :
- S = 2.π.a² + 2.π.a.b.[ arcsin(e) / e]
Voir aussi
Notes et références
Liens internes
Catégories : Page à recycler (mathématiques) | Géodésie
Wikimedia Foundation. 2010.
