Ellipse (mathématiques)

Pour les articles homonymes, voir Ellipse.

section du cône ou projection du cercle

Dans la vie courante, l’ellipse est la forme qu'on perçoit en regardant un cercle en perspective, ou la figure formée par l’ombre d'un disque sur une surface plane.

On retrouve aussi, en première approximation^[1], des ellipses dans les trajectoires des corps célestes (planètes, comètes ou satellites artificiels) en orbite autour d'une étoile ou d’une autre planète. Ainsi, la Terre parcourt-elle, en première approximation, une ellipse dont le Soleil est un foyer.

En mathématiques, une ellipse est une courbe plane fermée obtenue par la projection d’un cercle sur un plan — à condition que la direction de la projection ne soit pas parallèle au plan du cercle —, ou par l’intersection d’un cône droit avec un plan. Il faut alors que le plan ne soit pas trop penché c'est-à-dire que l'angle entre la normale au plan et l'axe du cône soit inférieur au complémentaire de l'angle du cône (angle entre l'axe de cône et une directrice).

En géométrie, elle est le lieu des points dont la somme des distances à deux points fixes, dits foyers, est constante (sa construction par la méthode du jardinier est très simple).

Une ellipse est aussi une conique d'excentricité comprise entre 0 et 1 (bornes normalement non incluses).

Le cercle est parfois considéré comme un cas particulier d’ellipse, mais souvent considéré plutôt (comme aussi le segment de droite) comme une ellipse dégénérée puisque certaines propriétés métriques de l'ellipse ne s'appliquent pas au cercle, sans une extension du plan affine avec un point supplémentaire à l'infini et une modification d'un des postulats de la géométrie euclidienne classique (par exemple la construction par ligne directrice est impossible pour le cercle dans le plan affine ; et comme les deux foyers s'y superposent au centre, le cercle n'a pas d'axe focal bien défini non plus).

Définitions géométriques

Construction d'une ellipse par section d'un cône.

Section d’un cône

L’ellipse est une courbe plane qui fait partie de la famille des coniques. Elle est obtenue par l’intersection d'un plan avec un cône de révolution (non dégénéré à une droite ou un plan) lorsque ce plan traverse de part en part le cône.

Le cercle est alors un cas particulier de l'ellipse (quand le plan de coupe est perpendiculaire à l'axe du cône, sans passer toutefois par son sommet).

Construction d'une ellipse par foyer et directrice. Ici avec une excentricité de 1/2.

Directrice et foyer

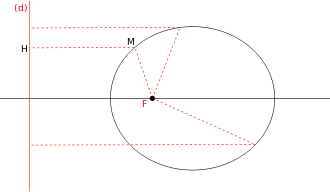
Le cadre est l'espace affine euclidien de dimension 2. Soient (d) une droite, F un point n'appartenant pas à (d), e un réel dans ]0,1[. Soit P le plan affine déterminé par (d) et F. On appelle ellipse de droite directrice (d), de foyer F et d'excentricité e l'ensemble des points M du plan P vérifiant :

$\frac{{\rm d}(M, F)}{{\rm d}(M, (d))} = e$

où d(M,F) mesure la distance du point M au point F et d(M,(d)) = d(M,H) celle de M à la droite (d).

La constante e de proportionnalité des deux distances, appelée excentricité de l’ellipse, est sans dimension ; elle est caractéristique de la forme de l'ellipse, indépendamment de ses isométries (translations et/ou rotations) ou homothéties (de rapport non nul) dans le plan affine, et donc du choix arbitraire de repère orthonormé pour ce plan ; elle détermine tous les autres rapports de distances (et toutes les différences angulaires) mesurés sur l'ellipse (par exemple son rapport d'aspect).

En conséquence, une ellipse est également entièrement déterminée par la position de ses foyers et son excentricité, ou bien encore par la position de ses droites directrices (parallèles entre elles), la position de son point central et son excentricité.

Notons K le projeté orthogonal de F sur (d). (KF) est alors clairement un axe de symétrie de l'ellipse appelé axe focal.

Toute ellipse (qui n’est pas un cercle) a deux droites directrices, parallèles entre elles, orthogonales à l’axe focal, et à distances égales du petit axe de l’ellipse.

En géométrie euclidienne, dans un espace plan à courbure nulle, le cercle qui n’a pas d’axe focal bien défini, n’a aucune droite directrice ; en géométrie non euclidienne, ses droites directrices, si elles existent, sont renvoyées à l’infini (par exemple en géométrie sphérique, dans un espace plan à courbure positive, les « droites » directrices existent dans n’importe quelle direction, mais se réduisent à un seul point à l’infini ; en géométrie hyperbolique, dans un espace plan à courbure négative, il existe pour le cercle une infinité de droites directrices, qui ne se superposent pas nécessairement mais sont elles aussi à distance infinie du centre de l’ellipse, de ses foyers ou de n’importe lequel de ses points).

Construction de l'ellipse par deux foyers et une corde de longueur constante

Définition bifocale de l'ellipse

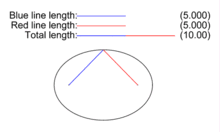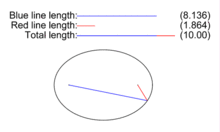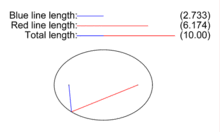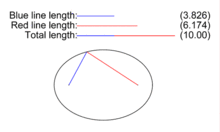
Soient F et F'' deux points distincts du plan. On appelle ellipse de foyers F et F'', l'ensemble des points M du plan vérifiant la propriété suivante :

${\rm d}(M, F) + {\rm d}(M, F') = 2a = 2\sqrt{c^2 + b^2},\quad a \in\R^*_+,\quad b \in\R^*_+$

où 2a est la longueur du grand axe, 2c = d(F,F'') et 2b est la longueur du petit axe (perpendiculaire au grand axe). Cette relation exprime que la somme des distances d'un point M aux foyers est constante et vaut la longueur du grand axe.

L'ellipse et les deux cercles de l'affinité

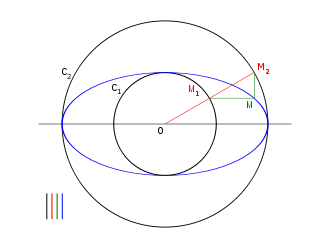
Image d'un cercle par une affinité

Soient (C1) un cercle de centre O et de rayon b, (C2) un cercle de centre O et de rayon a (b < a) et (xx') une droite passant par O. On appelle ellipse de centre O, de demi-grand axe a et de demi-petit axe b l'image du cercle (C2) par l'affinité d'axe (xx'), de direction perpendiculaire à (xx') et de rapport b /a.

Pour construire le point M de l'ellipse, image du point M₂ du grand cercle, on construit le point M₁ du cercle (C1) situé sur [OM₂]. On mène par M₂ une perpendiculaire à (xx') et par M₁ une parallèle à (xx'). Les droites se coupent en M. En effet, si m est le projeté orthogonal de M₂ sur (xx'), on a, d'après le théorème de Thalès,

$\frac{m'M}{m'M_2} = \frac{OM_1}{ OM_2 } = \frac{b}{a}$

Ellipse et une portion de son cercle directeur

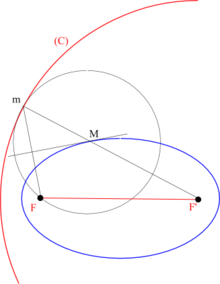
Construction par un cercle directeur

Soient F et F' deux points distincts, (C) un cercle de centre F' et de rayon 2a (2a > FF').

On appelle ellipse de cercle directeur (C) et de foyer F, l'ensemble des centres des cercles tangents à (C) et passant par F.

Pour construire le point M sur l'ellipse, centre du cercle tangent à (C) en m, on trace la médiatrice du segment [Fm] : cette médiatrice rencontre le rayon [F'm] en M (le centre du cercle tangent) ; cette médiatrice est aussi une tangente en M de l’ellipse.

Toute ellipse non dégénérée (qui n’est ni un cercle ni un segment) a deux cercles directeurs de rayons identiques, symétriques par rapport au petit axe, chacun centré sur un des foyers.

En géométrie euclidienne, le cercle n’a lui-même aucun cercle directeur ; en géométrie non euclidienne, les « cercles » directeurs d’un cercle, s’ils existent, sont concentriques et se « superposent » avec un même rayon infini (par exemple, en géométrie sphérique, dans un espace plan fermé par une courbure positive, ces cercles directeurs se réduisent au seul point à l’infini ; en géométrie hyperbolique, dans un plan ouvert avec une courbure négative, il existe une infinité de ces cercles directeurs (de rayon infini, mais qui ne se superposent pas nécessairement).

L’ellipse dégénérée à un seul segment (joignant ses foyers) a également ses deux cercles directeurs superposés, leur diamètre est ce segment.

Propriétés géométriques

Éléments de symétrie

« L’axe focal » (FF'), aussi appelé « axe principal », passant par les foyers et perpendiculaire aux directrices, est un axe de symétrie de l'ellipse ; il en est de même pour « l'axe secondaire », perpendiculaire à l'axe focal et passant par le « centre de l'ellipse » au milieu du « segment focal » [FF'].

L'intersection de l'axe focal et de l'axe secondaire, au centre de l'ellipse, est aussi un centre de symétrie.

Les points d'intersection de l'ellipse avec son axe focal sont appelés sommets principaux, ceux de l'ellipse avec son axe secondaire sont les sommets secondaires.

Le segment diamétral qui joint les sommets principaux (respectivement secondaires) en passant par le centre de l'ellipse est appelée « grand axe » (respectivement « petit axe »), comme aussi toute mesure de sa longueur une fois fixée l'unité arbitraire de longueur.

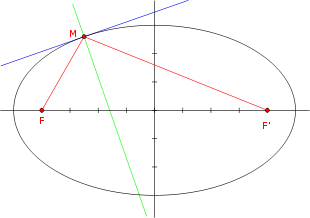La bissectrice du secteur angulaire formé par les droites reliant un point de l'ellipse aux foyers est perpendiculaire à la tangente en ce point.

Tangente et bissectrice

Soit une ellipse dont les foyers sont F et F'. En un point M de cette ellipse, considérons la bissectrice du secteur angulaire (FMF'). Alors, cette bissectrice est perpendiculaire à la tangente en M.

Cette propriété est utilisée en optique géométrique dans les miroirs elliptiques : un rayon lumineux qui passe par un des foyers, lorsqu'il est réfléchi, passe par l'autre foyer. Ainsi, si l'on met une ampoule à un foyer d'un miroir elliptique, le faisceau lumineux se concentre sur l'autre foyer.

Ceci explique également le fait que les sons se propagent très bien d'un quai à l'autre du métro parisien. En effet, la plupart des stations ont une forme elliptique. Si la source d'un son se trouve à un des foyers, tous les sons réfléchis vont converger vers l'autre foyer (sur l'autre quai). Cette propriété possédée par l'ellipse est aussi appelée « propriété de réflexivité » et s'explique en se servant de la tangente en un point de l'ellipse : de cette façon, un son ou un rayon lumineux émis d'un des foyers sera réfléchi sur l'autre foyer. Cette propriété est exploitée dans la conception de certains instruments d'optique. Elle est évidemment présente dans une galerie à écho, c'est-à-dire dans une pièce dont le plafond, par sa forme elliptique, fait qu'une personne qui chuchote en l'un des foyers est entendue en l'autre foyer. La rotonde du Capital Building à Washington et le Mormon Tabernacle à Salt Lake City sont des exemples de cette sorte de galeries^[2].

Une ellipse avec ses axes, son centre, un foyer et la directrice associée

Rapport entre les grandeurs

Les grandeurs (géométriques ou numériques) d’une ellipse sont :

• la longueur du grand rayon (ou demi-grand axe), généralement notée a ;
• la longueur du petit rayon (ou demi-petit axe), généralement notée b ;
• la distance séparant le centre de l'ellipse et un des foyers, généralement notée c ;
• le rayon d'un des deux cercles directeurs, généralement noté r=c+a (longueur du segment [FA’], F étant le centre d’un des cercles) ;
• la distance séparant un foyer F de sa directrice (d) associée, généralement notée h ;
• la distance moyenne séparant un point de l’ellipse à une de ses deux directrices, généralement notée f ;
• l'excentricité de l’ellipse (strictement comprise entre 0 et 1), généralement notée e ;
• le « paramètre » de l’ellipse, généralement noté p.

Des relations existent entre ces grandeurs :

• si l’ellipse est définie par son excentricité e et la distance h entre le foyer F et la directrice (d), alors :

  $a = {e h \over 1 - e^2} ,\, b = {e h \over \sqrt{1 - e^2}} ,\, c = {e^2 h \over 1 - e^2} ,\, r = {h \over 1 - e} ,\, f = {h \over 1 - e^2} ,\, p = e h \,;$

• si l’ellipse est donnée par ses rayons a et b où a > b :

  $c = \sqrt{a^2 - b^2} ,\, r = a + \sqrt{a^2 - b^2} ,\, h = {b^2 \over \sqrt{a^2 - b^2}} ,\, f = {a^2 \over \sqrt{a^2 - b^2}} ,\, e = {\sqrt{a^2 - b^2} \over a} ,\, p = {b^2 \over a} \,;$

• enfin, lorsque l’on connait le grand rayon a et l’excentricité e :

  $b = a \sqrt{1 - e^2} ,\, c = a e ,\, r = a(e + 1) ,\, h = {a(1 - e^2) \over e} ,\, f = {a \over e} ,\, p = a(1 - e^2) \,.$

Équations caractéristiques

Équation cartésienne

Dans le repère défini par le grand axe et le petit axe de l'ellipse, son équation est (si l'axe focal est x) :

$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ ;

si l'axe focal est y alors a et b sont inversés.

Si une ellipse n'est pas centrée à l'origine d'un système de coordonnées, mais que son grand axe et son petit axe restent parallèles aux axes des coordonnées, celle-ci peut être spécifiée par l'équation suivante :

$\frac{(x - u)^2}{a^2} + \frac{(y - v)^2}{b^2} = 1$

où les paramètres u et v sont les coordonnées du centre de l'ellipse.

Comme toute conique, une ellipse possède une équation de la forme :

$A x^2 + B xy + C y^2 + D x + E y + F = 0 \,$

B vaut 0 si les axes de l'ellipse sont parallèles à ceux de coordonnées.

Paramétrage

Dans un repère orthonormé du plan affine, dont les vecteurs directeurs sont parallèles aux axes de l'ellipse et où (u, v) sont les coordonnées du centre de l'ellipse, un paramétrage possible de l'ellipse est :

$[2] \qquad \begin{cases}x = u + a\cos t \\ y = v + b\sin t \end{cases} \quad t \in \R$

Ce paramétrage est périodique, de période 2π, ce qui signifie qu'on peut aussi le restreindre à un intervalle semi-ouvert de longueur minimale égale à cette période, par exemple à $t \in [0, 2\pi[$. Toute restriction du paramètre à un intervalle fermé de longueur inférieure donne un arc fermé ne parcourant qu'une partie de l'ellipse.

Équation polaire

$[3a] \qquad r(\theta) = \frac{p}{1+e \cos \theta} \qquad \theta \in\R$

dans le repère défini par le foyer et l'axe focal.

ou

$[3b] \qquad r^2(\theta) = \frac{b^2}{1-e^2 \cos ^2 \theta} \qquad \theta \in\R$

dans le repère défini par le centre et l'axe focal.

Circonférence

Soit une ellipse de demi grand axe $a\,$ et de demi petit axe $b\,$, dont l’excentricité est donc $e = {\sqrt{a^2 - b^2} \over a}\,$.

Expressions exactes de la circonférence

Articles connexes : intégrale elliptique et fonction elliptique.

Il n'existe pas de formule algébrique finie donnant la circonférence c de l'ellipse en fonction de deux de ses autres mesures caractéristiques ; en revanche elle peut-être donnée de façon non algébrique par :

$c = 4a \, {\rm E}(e)$,

où E est la fonction intégrale elliptique complète de deuxième espèce, également connue sous le nom de « module » de l’intégrale elliptique.^[3]

On peut aussi l'exprimer par :

$c = 2 \pi a \cdot {}_2{\rm F}_1\left(- \frac12, \frac12 ; 1 ; e^2 \right)$,

où ₂F₁ est la série hypergéométrique de Gauss. En effet, une série exacte donnant sa valeur (établie en 1742 par Colin Maclaurin) est (noter que les puissances de e ne désignent pas e comme la base naturelle des exponentielles, mais bien l’excentricité de l’ellipse) :

$\begin{matrix} c & = & 2 \pi a \sum_{n=0}^{+\infty} \left[ \frac{ (2n)! }{ (2^n \cdot n!)^2 } \right]^2 \frac{-e^{2n}}{2n-1} \\ & = & 2 \pi a \left[ 1 - \left(\frac{1}{2}\right)^2 e^2 - \left(\frac{1 \cdot 3}{2 \cdot 4}\right)^2 \frac{e^4}{3} - \left(\frac{1 \cdot 3 \cdot 5}{2 \cdot 4 \cdot 6}\right)^2 \frac{e^6}{5} - \cdots \right] \\ & = & 2 \pi a \left[ 1 - \frac{1}{4}e^2 - \frac{3}{64}e^4 - \frac{5}{256}e^6 - \frac{175}{16384}e^8 - \frac{441}{65536}e^{10} \cdots \right] \end{matrix}$

Le principal défaut de la série ci-dessus est que sa convergence est si lente qu'elle est inutilisable pour une évaluation numérique très précise (notamment, la sommation progressive de termes correcteurs de plus en plus proches les uns des autres ne produit pas un résultat stable numériquement, ce qui fausse grossièrement les résultats à cause des erreurs d'arrondis dus à la limite de précision relative des nombres à virgule flottante). Elle reste toutefois utile sur le plan théorique car elle permet de comparer les autres formules donnant des approximations de la circonférence, puisqu'on peut toujours les développer sous forme de série de Taylor, et par différence déterminer la série de Taylor donnant les erreurs relatives commises par ces formules alternatives, en fonction de l'excentricité.

Une deuxième expression équivalente est donnée par une autre série géométrique exprimée non pas directement selon l’excentricité e mais selon un autre facteur h sans dimension, qui croit aussi avec l’excentricité (et dans le même intervalle de 0 pour le cercle à 1 pour l’ellipse dégénérée à un segment) :

$h = \left( {a - b \over a + b} \right)^2 = \left( {1 - \sqrt{1 - e^2} \over 1 + \sqrt{1 - e^2}} \right)^2 = \left({ 1 - \sqrt{1 - e^2} \over e }\right)^4$ ;

dans ce cas la série géométrique s’écrit telle que le coefficient de hⁿ est le carré d’un coefficient binomial rationnel (exprimé ci-dessous sous la forme d’une factorielle décroissante, généralisée aux non entiers avec la fonction Gamma qui permet d’en résoudre la valeur) :

$\begin{matrix} {\frac12 \choose n} = C_{1/2}^n & = & \left( \frac12 \right)_n = \left(\frac12\right) \left(\frac12 - 1\right) \left(\frac12 - 2\right) \cdots \left(\frac12 - n + 1\right) \\ & = & {\Gamma\left(\frac12 + 1\right) \over \Gamma\left(\frac12 - n + 1\right)} = {2n \choose n} {1 \over (1 - 2n) (-4)^n} = {(2n)! \over (n!)^2 (1 - 2n) (-4)^n} \end{matrix}$

et ainsi la circonférence s’écrit alors sous la forme de la série de Gauss-Kummer (initialement appelée série de Sir James Ivory qui l’a partiellement explicitée et publiée dans son mémoire en 1796, mais qui ne pouvait être entièrement résolue que grâce à la contribution significative d’Ernst Kummer en 1836 qui a établi des équivalences importantes entre plusieurs séries hypergéométriques, et grâce à d’autres égalités formulées par Gauss) :

$\begin{matrix} c & = & \pi (a + b) \sum_{n=0}^{+\infty} {\frac12 \choose n}^2 h^n = \pi (a + b) \sum_{n=0}^{+\infty} \left[{ (2n)! \over (n!)^2 (1 - 2n) (-4)^n }\right]^2 h^n \\ & = & \pi (a + b) \left[ 1 + {h \over 4} + {h^2 \over 64} + {h^3 \over 256} + {25h^4 \over 16384} + {49h^5 \over 65536} + \cdots \right] \end{matrix}$

Cette série a meilleure convergence que celle de Maclaurin sur la totalité de la plage des excentricités ; elle est très nettement plus rapide au moins pour les ellipses à faible excentricité (pas trop aplaties) pour lesquelles une évaluation numérique de cette série est stable numériquement (les erreurs d'arrondis ne se cumulent pas de façon significative), sinon le gain de convergence reste très modéré.

Aussi, pour les ellipses à forte excentricité, une autre approche est nécessaire en fonction de $x = 1 - e^2 = \left({b \over a}\right)^2$, qui est le carré du « rapport d’aspect » de l’ellipse (une mesure sans dimension qui décroit en sens inverse de l’excentricité, de 0 pour l’ellipse dégénérée du segment, à 1 pour le cercle). Dans ces condition, la circonférence est donnée par la série d’Arthur Cayley (établie en 1876) :

$c = 4a \left( 1 + \sum_{n = 1}^{+\infty} {x^n \over 2} \left[{ (2n)! \over (2^n n!)^2 }\right]^2 { 2n \over 2n - 1 } \left[ \ln\left({ 16 \over x }\right) - \left(\sum_{k = 1}^n{ 4 \over (2k - 1)2k }\right) + {2 \over (2n - 1)2n} \right] \right)$

qui se développe en :

$\begin{matrix} {c \over 4a} - 1 & = & { x \over 4} \left[ \ln\left({ 16 \over x }\right) - 1 \right] + { 3 x^2 \over 32} \left[ \ln\left({ 16 \over x }\right) - \frac{ 13}{ 16} \right] + { 15 x^3 \over 256} \left[ \ln\left({ 16 \over x }\right) - \frac{ 12}{ 5} \right] + {175 x^4 \over 4096} \left[ \ln\left({ 16 \over x }\right) - \frac{1051}{120} \right] + \cdots \\ & & + {x^n \over 2} {1^2 \over 2^2} {3^2 \over 4^2} \cdots {(2n - 3)^2 \over (2n - 2)^2}{(2n - 1) \over 2n} \left[ \ln\left({ 16 \over x }\right) - {4 \over 1\times 2} - {4 \over 3\times 4} - \cdots - {4 \over (2n - 3)(2n - 2)} - {2 \over (2n - 1)(2n)} \right] + \cdots \end{matrix}$

Cette série exacte converge pour toute la plage des excentricités, mais n’a une convergence excellente et bien plus rapide que les séries de Maclaurin et de Gauss-Kummer que pour les excentricités élevées, où elle est également stable numériquement. Dans les évaluations numériques rapides, on peut donc associer cette série de Cayley à la série de Gauss-Kummer plus simple à calculer et convergeant plus rapidement pour les excentricités faibles et modérées, en fixant arbitrairement la coupure entre les deux méthodes à une valeur d’excentricité voisine de 96% (qui correspond aussi à un rapport d’aspect b/a voisin de 28% ou une valeur de x voisine de 7,84%).

Plus généralement, la longueur de l'arc, comme une fonction de l'angle sous-tendu, est donnée par une intégrale elliptique incomplète de seconde espèce. La fonction réciproque, l'angle sous-tendu comme une fonction de la longueur de l'arc, est donnée par les fonctions elliptiques.

Expressions approchées de la circonférence

Une bonne approximation algébrique, fréquemment utilisée en cartographie pour la longueur d'un méridien terrestre (et simplifier certains calculs de distances), est donnée par la formule quadratique (ainsi nommée car elle est proportionnelle à une moyenne quadratique pondérée de la somme et de la différence du grand axe a et du petit axe b) :

$c \approx \pi \sqrt{ 2 (a^2 + b^2) - \frac12 (a - b)^2 }$

La même formule s’exprime aussi de façon équivalente en fonction de l'excentricité e :

$\begin{matrix} c \approx & & 2 \pi a \sqrt{ 3 + \sqrt{1 - e^2} - \frac{3}{2}e^2 } = 2 \pi a \left[ 1 - \frac{1}{4}e^2 - \frac{3}{64}e^4 - \frac{5}{256}e^6 - \frac{89}{8192}e^8 - \frac{231}{32768}e^{10} \cdots \right] \end{matrix}$

dont les 4 premiers termes de la série équivalente (jusqu’au sixième degré de e) sont corrects ; l'erreur commise par les coefficients incorrects des termes de degré supérieur donne une erreur relative très proche de $\frac{3}{16384}(1+2e^2)e^8$. Rapportée à la circonférence d'un méridien terrestre (dont l'excentricité est d'environ e=0,081819191...), l'erreur absolue produite par cette formule approchée serait inférieure à 15 µm (environ le dixième de l'épaisseur d'un cheveu humain).

Il existe d’autres formules similaires d'approximation de la circonférence, utilisant aussi une moyenne de Hölder pondérée, mais avec une valeur de l’exposant de Hölder différente de 2 (celle utilisée ci-dessus pour la formule quadratique) et qui permet de mieux approcher les termes dans la série équivalente et donc de donner une erreur relative minimale quelle que soit l'excentricité de l'ellipse. Aucune de ces formules ne peut toutefois donner une valeur exacte de la circonférence, on ne peut que déterminer une valeur d'exposant optimale.

Une autre approximation algébrique (améliorée d'au minimum deux ordres de grandeur dans le pire cas) est donnée par la première formule de Srinivasa Ramanujan :

$c \approx \pi \left[ 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right] = \pi (a + b) \left[ 3 - \sqrt{4 - h} \right]$,

où $h = \left( \frac{a - b}{a + b} \right)^2$ est un facteur positif sans unité, différent de l'excentricité (mais qui croît avec elle, entre 0 pour le cercle, qui est une ellipse dégénérée où les deux foyers sont confondus et les directrices renvoyées à l'infini, et 1 pour l'ellipse dégénérée plate, réduite au seul segment joignant ses foyers).

Cette formule s’écrit également, de façon équivalente :

$c \approx \pi a \left[ 3 (1+\sqrt{1-e^2}) - \sqrt{(3+ \sqrt{1-e^2})(1+3 \sqrt{1-e^2})} \right]$

Cette formule d'approximation est extrêmement précise, puisque les 6 premiers termes de la série génératrice sont corrects. Rapportée à la circonférence d'un méridien terrestre, l'erreur absolue produite par cette formule serait inférieure à 1,75 pm, soit environ le trentième du rayon de Bohr (celui de l'atome d'hydrogène dans son état fondamental au repos), donc une précision ridicule qui dépasse tout ce qui est réellement nécessaire pour la cartographie et ne correspond à aucune réalité mesurable, puisque à ce niveau de précision les circonférences moyennes des méridiens terrestres sont toutes différentes selon leur longitude et varient même au cours du temps (sous l'influence des marées influencées par les forces de gravitation de la lune, du soleil et d'autres objets massifs du système solaire, de la météorologie, de l'activité solaire, etc... et même de l'activité humaine), sachant aussi que l'excentricité des méridiens du géoïde terrestre n'est pas connue avec un niveau de précision compatible avec cette précision.

Une approximation algébrique encore meilleure est donnée par la deuxième formule de Srinivasa Ramanujan :

$c \approx \pi \left( a + b \right) \left[ 1 + {3h \over 10 + \sqrt{4 - 3h}} \right]$

où encore l'excentricité de l'ellipse est exprimée selon le même facteur $h = \left( \frac{a - b}{a + b} \right)^2$ que dans la formule précédente.

Cette formule est d’une remarquable précision puisque son développement exprimé sous forme d'une série exponentielle de base e² fournit les coefficients des premiers termes de la série de façon exacte jusqu’au coefficient de e¹⁸ inclus. L’erreur relative sur l’estimation du périmètre de l'ellipse théorique modélisant un méridien terrestre moyen est alors de l'ordre de seulement − 3 / 2³⁷e²⁰. Dans notre Univers physique (celui où nous vivons), l'espace cesse d'être mesurable de façon continue et linéaire à une distance connue comme la longueur de Planck qui est d’environ 1,616×10^-35 m ; pourtant si on essaye d'estimer la circonférence d'un méridien terrestre modélisé comme une ellipse parfaite, l'erreur relative commise ne serait alors que de 6,5×10^-44 et l’erreur absolue de cette estimation par rapport à la circonférence exacte de cette ellipse ne dépasserait pas environ 3 800 fois la longueur de Planck : cette erreur de longueur est énormément plus petite que le rayon atomique (lequel se mesure de l'ordre du rayon de Bohr défini pour l'atome d'hydrogène) et on atteint des mesures à une échelle quantique (même très inférieure à la distance moyenne séparant un neutron et un proton dans un noyau de deutérium, un des isotopes de l'hydrogène) ; à cette échelle de longueur, la géométrie cartésienne classique ne s'applique plus du tout (les « distances » à cette échelle ne sont plus ni transitives ni linéaires, ce ne sont que des longueurs probabilistes avec une incertitude très significative inhérente à toute mesure, et qui doivent aussi prendre en compte la courbure de l'Univers de la relativité générale, étant donné les vitesses relatives des sous-particules impliquées, ainsi aussi qu'une quantification de la gravité, et donc aussi de l'espace-temps déjà courbé dans la relativité générale).

Aire du domaine intérieur à une ellipse

Il existe différentes manières de calculer l'aire d'une ellipse. On peut se placer dans le repère porté par les axes où l'équation de l'ellipse s'écrit :

$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$

Avec les symétries établies plus haut, il suffit de calculer par exemple l'aire de la portion d'ellipse dans le quart supérieur droit du plan rapporté à ce repère. L'équation de la portion d'ellipse correspondante est :

$y= b \sqrt{1 - \left(\frac xa\right)^2}$

pour x dans [0,a]. D'où l'aire du quart supérieur droit d'ellipse :

$I = \int_0^a b \sqrt{1-\left(\frac xa\right)^2}\,\mathrm dx = ab \int_0^1 \sqrt{1- t^2}\,\mathrm dt = ab \int_0^{\frac\pi2} \cos^2 u\,\mathrm du$

la dernière réécriture obtenue avec le changement de variable $u \mapsto \sin u = t$ de [0,π / 2] sur [0,1]. Reste à linéariser cos ²u pour trouver le quart de l'aire d'une ellipse :

$I= ab \int_0^{\frac\pi2} \frac{1+ \cos 2u}2\,\mathrm du = \frac{\pi ab}4$

et pour l'aire de toute l'ellipse :

S = πab

Remarquer que pour a = b, on retrouve l'aire du disque.

Tracer une ellipse

• Méthode des deux points et de la corde : selon la définition bifocale, la somme AF + AF' des distances entre un point A de l'ellipse et ses deux foyers F et F' est constante. Ainsi, on plante deux piquets dans le sol (les deux foyers), on prend une corde non élastique de longueur donnée (la somme constante) que l'on attache aux piquets ; le trajet que l'on parcourt en maintenant la corde tendue est une ellipse. On nomme cette technique celle de « l'ellipse du jardinier ».
• 

  Ellipse servant à représenter un perçage droit vu en perspective (figure de droite) ; le trait d'axe vertical figure l'axe du perçage
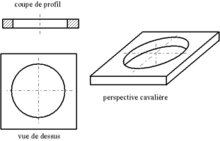
  En dessin industriel, une ellipse est en général un cercle vu en perspective (une pièce est rarement elliptique même si ce n'est pas exclu), ou bien un perçage en biais par rapport à la surface de la pièce.

Ellipse servant à représenter un perçage oblique vu de face (figure de droite)

L'ellipse se représente donc avec les mêmes traits d'axe que pour le cercle. Dans le cas d'un cercle vu en perspective, ces traits d'axe sont inclinés et suivent les directions de référence. Dans le cas d'une forme réellement elliptique, les traits d'axes sont perpendiculaires.

• 

  Tracé d'une ellipse à main levée à l'aide d'un parallélogramme
  Tracé à main levée, méthode du parallélogramme exinscrit : on a vu ci-dessus qu'une ellipse pouvait être considérée comme un cercle vu en perspective.

De même qu'un cercle est inscrit dans un carré, une ellipse est inscrite dans un parallélogramme qui n'est autre que ce carré vu en perspective cavalière (notez qu'il existe une infinité de parallélogrammes circonscrits, il suffit d'en choisir un). On trace d'abord un parallélogramme, on le divise en quatre quartiers selon les parallèles aux côtés passant par les milieux des autres côtés ; dans chaque quartier, on trace un arc passant par les milieux des côtés et tangent aux côtés en ces milieux (certaines caractéristiques de sécantes dans le cercle permettent de trouver d'autres points de passage intermédiaires de ces arcs).

Notes et références

1. ↑ voir problème à deux corps et problème à N corps
2. ↑ Swokowski (trad. Micheline Citta), Analyse, 5^e édition
3. ↑ Attention aux confusions sur la notation de la fonction E ; par exemple dans le programme Mathematica et sur le site Wolfram, on trouve définie une fonction EllipticE similaire, mais différente, ${\rm EllipticE}(x) = {\rm E}(\sqrt x)$, de sorte que la formule à utiliser est alors $c = 4a \, {\rm EllipticE}(e^2)$.

Voir aussi

Articles connexes

• Coniques
  • Hyperbole
  • Parabole
• Ovale
• Théorème de Marden
• Ellipsographe d'Archimède (en)

Liens externes

• Propriétés de l'ellipse avec démonstrations
• Cours de géométrie de M. Gerhard Wanner de l'université de Genève, section de mathématiques
• (en)Construire la géométrie analytique objets
• Sections d'un cône et théorème de Dandelin