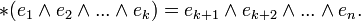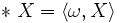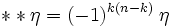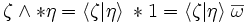- Dualite de Hodge
-
Dualité de Hodge
En algèbre linéaire, l'opérateur de Hodge est un opérateur sur l'algèbre extérieure d'un espace vectoriel euclidien orienté. Il est usuellement noté par une étoile qui précède l'élément auquel l'opérateur est appliqué. On parle ainsi d'étoile de Hodge. Si la dimension de l'espace est n, l'opérateur établit une correspondance entre les k-vecteurs et les (n-k)-vecteurs, appelée dualité de Hodge.
En géométrie différentielle, l'opérateur de Hodge peut être étendu aux fibrés vectoriels riemanniens orientés. Appliqué à l'espace cotangent des variétés riemanniennes orientées, l'opérateur de Hodge permet de définir une norme L2 sur l'espace des formes différentielles. La codifférentielle se définit alors comme l'adjoint forme de la dérivée extérieure. Cette codifférentielle intervient notamment dans la définition des formes harmoniques.
Sommaire
Définition
Opérateur de Hodge sur les k-vecteurs
Soit E espace vectoriel euclidien orienté de dimension finie n. Les sous-espaces ΛkE et Λn − kE des k-vecteurs et des n-k vecteurs sont de même dimension, à savoir Cnk. Il est possible de définir un isomorphisme linéaire noté * entre ces deux espaces et appelé opérateur de Hodge.
Pour toute base orthonormale directe e1,e2,...,en,
Il s'étend ensuite par linéarité à toute l'algèbre extérieure. Cette définition est peu satisfaisante puisqu'elle fait intervenir des bases et pose un problème de compatibilité. Elle a néanmoins l'avantage de bien décrire le comportement de l'opérateur de Hodge sous forme de complétion de base orthonormale directe.
Une définition plus convenable consiste à faire intervenir la forme volume ω de l'espace vectoriel euclidien orienté E. Le dual de Hodge s'obtient en effectuant la contraction
Dualité
Pour un k-vecteur
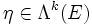 de l'espace E de dimension n, appliquer deux fois l'opérateur de Hodge donne l'identité, au signe près
de l'espace E de dimension n, appliquer deux fois l'opérateur de Hodge donne l'identité, au signe prèsApplications
Produit scalaire sur l'algèbre extérieure
L'opérateur de Hodge permet de définir un produit scalaire sur l'algèbre extérieure par la relation
Pour ce produit scalaire, les k-vecteurs obtenus par produit extérieur à partir de la base orthnormale de E constituent une base orthonormale de ΛE.
Codifférentielle
Extension aux espaces quadratiques
Il est possible de définir un opérateur de Hodge pour un espace quadratique. La formule de dualité est alors modifiée pour prendre en compte la signature de la forme quadratique sur E. Précisément, on multiplie le second membre par le discriminant de cette forme quadratique. Ainsi si n=4 et si la signature est (+,−,−,−) ou (−,+,+,+), l'exposant est k(n-k)+1.
Références
Ouvrages
- (en) Jürgen Jost, Riemannian Geometry and Geometric Analysis [détail des éditions]
- Sylvestre Gallot, Dominique Hulin, Jacques Lafontaine ; Riemannian Geometry [détail des éditions]
- (en) Marcel Berger, A Panoramic View of Riemannian Geometry [détail des éditions]
Notes et références
- Portail des mathématiques
Catégories : Algèbre multilinéaire | Géométrie différentielle | Géométrie riemannienne
Wikimedia Foundation. 2010.