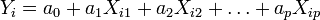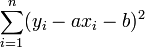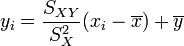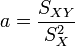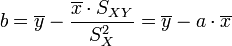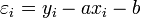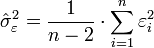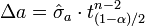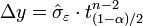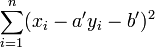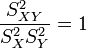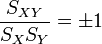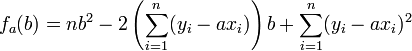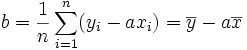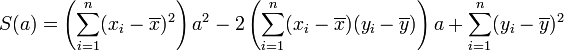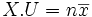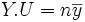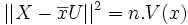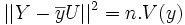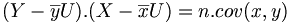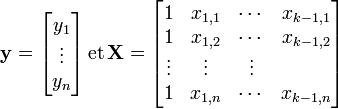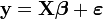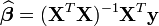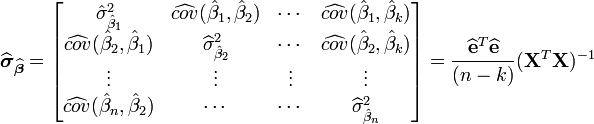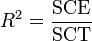- Droite de régression
-
Régression linéaire
 Pour les articles homonymes, voir Régression.
Pour les articles homonymes, voir Régression.En statistiques, étant donné un échantillon aléatoire
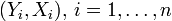 un modèle de régression simple suppose la relation affine suivante entre Yi et Xi:
un modèle de régression simple suppose la relation affine suivante entre Yi et Xi:La régression linéaire consiste à déterminer une estimation des valeurs a et b et à quantifier la validité de cette relation grâce au coefficient de corrélation linéaire. La généralisation à p variables explicatives de ce modèle est donnée par
et s'appelle la régression linéaire multiple.
Sommaire
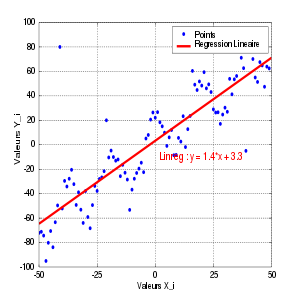
Situation
Empiriquement, à partir d'observations
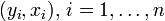 , on a représenté dans un graphe l'ensemble de ces points représentant des mesures d'une grandeur yi en fonction d'une autre xi, par exemple la taille yi des enfants en fonction de leur âge xi.
, on a représenté dans un graphe l'ensemble de ces points représentant des mesures d'une grandeur yi en fonction d'une autre xi, par exemple la taille yi des enfants en fonction de leur âge xi.Les points paraissent alignés. On peut alors proposer un modèle linéaire, c'est-à-dire chercher la droite dont l'équation est yi = axi + b et qui passe au plus près des points du graphe.
Passer au plus près, selon la méthode des moindres carrés, c'est rendre minimale la somme des carrés des écarts des points à la droite
où (yi - axi - b)² représente le carré de la distance verticale du point expérimental (yi,xi) à la droite considérée comme la meilleure.
Cela revient donc à déterminer les valeurs des paramètres a et b (respectivement le coefficient directeur de la droite et son ordonnée à l'origine) qui minimisent la somme ci-dessus.
Définitions
- Moyenne empirique des xi :
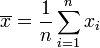 .
. - Moyenne empirique des yi :
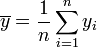 .
. - Point moyen:
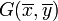 .
. - Variance empirique des xi :
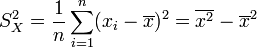 .
. - Ecart-type empirique des xi :
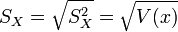 .
. - Variance empirique des yi :
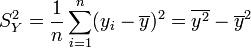 .
. - Ecart-type empirique des yi :
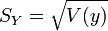 .
. - Covariance empirique des xi, yi :
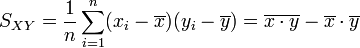 .
.
La formule de la variance se retient par la mnémonique : La moyenne des carrés moins le carré de la moyenne
de même pour la covariance : La moyenne du produit moins le produit des moyennes.
Résultat de la régression
La droite rendant minimale la somme précédente passe par le point G et a pour coefficient directeur
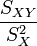 . Son équation est donc :
. Son équation est donc :soit
Erreur commise
Si l'on appelle εi l'écart vertical entre la droite et le point (xi , yi )
alors l'estimateur de la variance résiduelle σ²ε est :
la variance de a, σ²a , est estimée par
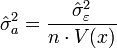 .
.
On est dans le cadre d'un test de Student sur l'espérance avec écart type inconnu. Pour un niveau de confiance α donné, on estime que l'erreur sur a est :
où tn-2(1-α)/2 est le quantile d'ordre α/2 de la loi de Student à n-2 degrés de liberté.
L'erreur commise en remplaçant la valeur mesurée yi par le point de la droite axi + b est :
À titre d'illustration, voici quelques valeurs de quantiles.
Exemples de quantiles de la loi de Student n niveau de confiance 90 % 95 % 99 % 99,9 % 5 2,02 2,57 4,032 6,869 10 1,812 2,228 3,169 4,587 100 1,660 1,984 2,626 3,390 Lorsque le nombre de points est important (plus de 100), on prend souvent une erreur à 3σ, qui correspond à un niveau de confiance de 99,7 %.
Voir aussi : Erreur (métrologie).
Coefficient de corrélation linéaire
On peut aussi chercher la droite D' : x = a'y + b' qui rende minimale la somme :
On trouve alors une droite qui passe aussi par le point moyen G et telle que
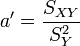 .
.
On souhaite évidemment tomber sur la même droite. Ce sera le cas si et seulement si
- a' = 1/a,
c'est-à-dire si
- aa' = 1.
Les droites sont confondues si et seulement si
c'est-à-dire si et seulement si
On appelle cette quantité
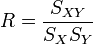 le coefficient de corrélation linéaire entre x et y. On peut démontrer que ce nombre est toujours compris entre -1 et 1.
le coefficient de corrélation linéaire entre x et y. On peut démontrer que ce nombre est toujours compris entre -1 et 1.En pratique sa valeur absolue est rarement égale à 1, mais on estime généralement que l'ajustement est valide dès que ce coefficient a une valeur absolue supérieure à
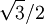
Voir également : Corrélation (mathématiques).
Démonstration des formules par étude d'un minimum
Pour tout réel a, on pose
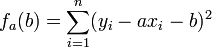 . Il suffit de développer et ordonner ce polynôme du second degré en b. On obtient:
. Il suffit de développer et ordonner ce polynôme du second degré en b. On obtient:Ce polynôme atteint son minimum en
Ce qui signifie que la droite passe par le point moyen G
Il reste à remplacer dans la somme de départ, b par cette valeur.
Pour tout réel a,
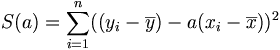 . Il suffit de développer et ordonner ce polynôme du second degré en a. On obtient
. Il suffit de développer et ordonner ce polynôme du second degré en a. On obtient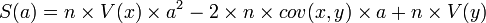 .
.
Ce polynôme atteint son minimum en
La droite de régression est bien la droite passant par G et de coefficient directeur
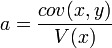 .
.Démonstration des formules grâce aux espaces vectoriels de dimension n
Dans l'espace
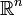 , muni du produit scalaire canonique, on considère le vecteur X de coordonnées (x1,x2,...,xn), le vecteur Y de coordonnées (y1,y2,...,yn), le vecteur U de coordonnées (1, 1, ..., 1).
, muni du produit scalaire canonique, on considère le vecteur X de coordonnées (x1,x2,...,xn), le vecteur Y de coordonnées (y1,y2,...,yn), le vecteur U de coordonnées (1, 1, ..., 1).On peut remarquer que :
On note alors
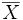 le vecteur
le vecteur 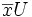 et
et 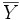 le vecteur
le vecteur 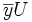
Le vecteur Z de coordonnées (ax1 + b,ax2 + b,...,axn + b) appartient à l'espace vectoriel engendré par X et U.
La somme
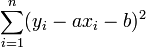 représente le carré de la norme du vecteur Y − Z.
représente le carré de la norme du vecteur Y − Z.Cette norme est minimale si et seulement si Z est le projeté orthogonal de Y dans l'espace vectoriel vect(X,U).
Z est le projeté de Y dans l'espace vectoriel vect(X,U) si et seulement si (Z − Y).U = 0 et
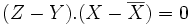 .
.Or
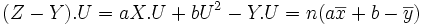 donc (Z-Y).U=0 signifie que
donc (Z-Y).U=0 signifie que 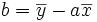 .
.En remplaçant dans
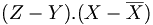 , on obtient
, on obtient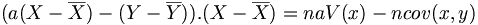 donc
donc 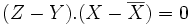 signifie que
signifie que 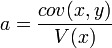
Enfin le coefficient de corrélation linéaire s'écrit alors
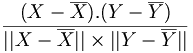 . Cette quantité représente le cosinus de l'angle formé par les vecteurs
. Cette quantité représente le cosinus de l'angle formé par les vecteurs 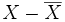 et
et 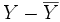 .
.On retrouve alors les résultats suivants:
- si le coefficient de corrélation linéaire est 1 ou -1, les vecteurs
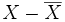 et
et 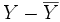 sont colinéaires de coefficient de colinéarité a et
sont colinéaires de coefficient de colinéarité a et 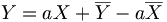 . L'ajustement linéaire est parfait.
. L'ajustement linéaire est parfait. - si le coefficient de corrélation linéaire est en valeur absolue supérieur à
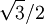 alors l'angle formé par les deux vecteurs est compris entre − π / 6 et π / 6 ou entre 5π / 6 et 7π / 6.
alors l'angle formé par les deux vecteurs est compris entre − π / 6 et π / 6 ou entre 5π / 6 et 7π / 6.
Généralisation: le cas matriciel
Article détaillé : Régression linéaire multiple.Lorsqu'on dispose de plusieurs variables explicatives dans une régression linéaire, il est souhaitable d'avoir recours aux notations matricielles. Si l'on dispose d'un jeu de n données (yi)i = 1..n que l'on souhaite expliquer par k variables explicatives (y compris la constante)
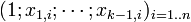 , on peut poser:
, on peut poser:La régression linéaire s'exprime sous forme matricielle:
et il est question d'estimer le vecteur de coefficients k × 1
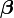 .
.Son estimateur par moindre carré est:
Il faut que la matrice X soit de plein rang (
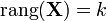 ) afin que
) afin que 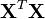 soit inversible.
soit inversible.L'estimation de la matrice (symétrique) de variance-covariance de cet estimateur est:
Le terme
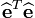 représente la somme des carrés des résidus
représente la somme des carrés des résidus 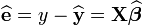 .
.La qualité de l'ajustement linéaire se mesure encore par un coefficient de corrélation R2, défini ici par:
où SCE (respectivement SCT) représente la somme des carrés expliqués (respectivement la somme des carrés totaux). Ces sommes se donnent par
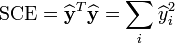 et
et 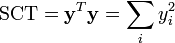 .
.Voir aussi
- Statistiques
- Statistique (mathématiques élémentaires)
- Régression mathématique
- Corrélation (mathématiques)
- Régression linéaire multiple, la généralisation à p variables explicatives de la régression linéaire
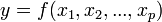 .
. - Modèles de régression multiple postulés et non postulés
Liens externes
- http://yves.demur.free.fr/guppy/file/reglin/reglin0108.pdf (utilisation pratique de la régression linéaire, + programmes test en C sur le site http://yves.demur.free.fr/guppy/articles.php?lng=fr&pg=84)
- http://www.unilim.fr/pages_perso/jean.debord/math/reglin/reglin.pdf La régression linéaire
- Portail des probabilités et des statistiques
Catégorie : Estimation (statistique)
Wikimedia Foundation. 2010.