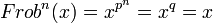- Corps de Galois
-
Corps fini
En mathématiques et plus précisément en algèbre, un corps fini est un corps (commutatif) dont le cardinal est fini. À isomorphisme près, un corps fini est entièrement déterminé par son cardinal qui est toujours de la forme pn, une puissance d'un nombre premier. Ce nombre premier n'est autre que sa caractéristique et le corps se présente comme l'unique extension simple du corps premier Z/p.Z de dimension n.
Les applications sont essentiellement la théorie algébrique des nombres où les corps finis apparaissent comme une structure essentielle à la géométrie arithmétique. Cette branche a permis, entre autres, de démontrer le grand théorème de Fermat. Les corps finis sont fréquemment utilisés en cryptographie ou en théorie des codes, par exemple, pour déterminer des codes correcteurs efficaces.
Remarque sur la terminologie : la convention la plus usitée en France[1], même si elle n'est pas générale, utilise le mot « corps » que la loi de multiplication soit commutative ou non, ce qui oblige à préciser si le corps est commutatif on non. C'est celle utilisée dans les quatre références de l'article. Elle diffère de la convention courante en anglais où « field » sous-entend déjà la commutativité. Dans le cas des corps finis, la convention est en fait de peu d'importance car, d'après le théorème de Wedderburn, tout corps fini est commutatif. Ce résultat se démontre à l'aide des polynômes cyclotomiques.
Sommaire
Histoire
Théorie
La théorie générale des corps apparaît initialement durant la seconde moitié du XIXe siècle. Richard Dedekind (1831-1916) invente le terme allemand de Körper[2], terme encore utilisé aujourd'hui, dont la traduction française est corps. Une première définition est l'œuvre[3] de Heinrich Weber (1842-1913). La définition axiomatique moderne est due à Ernst Steinitz (1871-1928) et date de 1910.
Les travaux de Frobenius (1849-1917) marquent le début d'une utilisation des corps finis non premiers. Ils apparaissent nécessaires pour la résolution de questions[4] sur la théorie des représentations d'un groupe fini. L'endomorphisme de Frobenius permet d'appliquer la théorie de Galois à ces structures. La théorie se montre redoutablement efficace, dans le cas commutatif. L'existence, le cardinal et la structure des corps finis sont rapidement déterminés. Pour cette raison, deux termes deviennent synonymes, corps de Galois et corps fini.
L'étude systématique des corps finis commence au début du XXe siècle, avec les travaux de Leonard Dickson (1874-1954) puis de Joseph Wedderburn (1882-1948). Dickson publie[5] la première classification des corps finis commutatifs. La structure de l'anneau des polynômes associé y est explicitée. La question du cas non commutatif est alors l'objet d'une conjecture: il n'existe pas de corps fini non commutatif. Wedderburn, séjourne à l'Université de Chicago en 1904 et travaille en étroite collaboration avec Dickson. À son retour, l'année suivante, il démontre la conjecture qui devient un théorème, nommé en son honneur.
Depuis cette époque, la théorie proprement dite ne comporte plus de problème ouvert. En revanche, les applications, tant théoriques que pratiques, abondent durant tout le XXe siècle.
Applications théoriques
Les corps finis sont, en particulier, utilisés en arithmétique, au fondement par exemple de l'arithmétique modulaire. Elle a permis à Gauss (1777-1865) de démontrer[6] la loi de réciprocité quadratique. La structure de corps intervient notamment dans le résolution d'équations diophantiennes (voir section Applications). Le petit théorème de Fermat est un exemple archétypal.
Artin (1898-1962) utilise le fait qu'un contexte naturel des lois de réciprocité est celui des corps finis. C'est l'un des outils qui lui permettent de résoudre le neuvième problème de Hilbert. Il initie l'analyse de l'équivalent de la fonction zêta de Riemann sur les corps finis. La géométrie arithmétique se généralise sur des structures finies. Cette approche est particulièrement active durant la seconde moitié du XXe siècle. André Weil (1906, 1998) généralise la démarche aux courbes algébriques et Pierre Deligne (né en 1944) aux variétés algébriques. Les conjectures de Weil sur les variétés sur des corps finis, énoncées en 1940 par André Weil, font partie des problèmes importants de cette époque. Démontrées en 1974, elles ouvrent la voie au théorème de Taniyama-Shimura démontré par Andrew Wiles et ayant pour conséquence le grand théorème de Fermat, souvent cité dans les articles de vulgarisation.
Applications pratiques
Après la Seconde Guerre mondiale et pour les besoins de la société, Claude Shannon (1916, 2001) formalise la théorie de l'information comme une branche des mathématiques[7], posant les problématiques de la sécurité[8] et de la fiabilité.
La cryptologie s'appuie sur la possibilité de générer rapidement de grands nombres premiers. La confidentialité d'un message est assurée par notre incapacité actuelle de casser des entiers, c'est-à-dire d'effectuer un algorithme permettant de décomposer un nombre en facteurs premiers en un temps raisonnable. Une recherche active cherche à créer de nouveaux algorithmes allant en ce sens. Ainsi, Michael Rabin (né en 1931) publie[9] un test de primalité se fondant sur les propriétés du groupe multiplicatif des corps premiers.
La fiabilité traite de la capacité à transmettre sans erreur un message malgré des altérations dans la communication, elle est traitée par la théorie des codes correcteurs. En 1950, Richard Hamming (1915-1998) travaille pour les laboratoires Bell avec Shannon sur ce sujet. Il utilise[10] des espaces vectoriels de dimension finie sur des corps finis pour formaliser un cadre opérationnel à la théorie et trouver les premiers exemples de codes correcteurs optimaux. Cette approche donne naissance à la théorie des codes linéaires.
En 1960, deux mathématiciens R. C. Bose, D. K. Ray-Chaudhuri montrent[11] que des idéaux de l'anneau des polynômes sur les corps finis de caractéristique deux sont particulièrement adaptés. La théorie est généralisée[12] par le mathématicien A. Hocquenghem et donne naissance à la famille de codes BCH. Deux autres fondateurs de la théorie, I. Reed et G. Solomon enrichissent la méthode[13] et créent des codes à même de résister à de grosses altérations, les codes de Reed-Solomon. Les applications les plus connues sont probablement le système de communication de certaines sondes de la NASA comme Voyager ou les disques compacts. Durant les années 1970 les résultats d'arithmétique avancés sur les courbes elliptiques des corps finis, trouvent leur application[14] avec, par exemple, les codes de Goppa.
La théorie des codes correcteurs est maintenant considérée comme une branche de celle des corps finis.
Exemples
Le plus petit corps
Le plus petit corps fini noté (
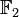 , +, . ) ou plus simplement F2 est composé de deux éléments distincts, à savoir l'élément neutre pour l'addition 0 et l'élément neutre pour la multiplication 1. Voici la définition des opérations « + » et « . » sur ce corps :
, +, . ) ou plus simplement F2 est composé de deux éléments distincts, à savoir l'élément neutre pour l'addition 0 et l'élément neutre pour la multiplication 1. Voici la définition des opérations « + » et « . » sur ce corps :+ 0 1 0 0 1 1 1 0 . 0 1 0 0 0 1 0 1 Corps finis complexes
Si p est un nombre premier congru à 3 modulo 4, et a et b des éléments du corps de congruences modulo p, les éléments de type a + i b constituent aussi un corps.
Corps premiers et extensions
Comme Z est un anneau euclidien, a fortiori principal, tout idéal I s'écrit de manière unique sous la forme I = n.Z où n est appelé le générateur positif de I. Par définition, c'est le plus petit entier positif non nul appartenant à I. Les seules structures quotients obtenues à partir de Z sont donc les anneaux commutatifs unitaires Z/n.Z.
Ces anneaux donnent les premiers exemples de corps finis :
-
- L'anneau Z/nZ est un corps si, et seulement si, n est un nombre premier.
Cette propriété est démontrée dans le paragraphe Cas où Z/nZ est un corps de l'article Anneau Z/nZ.
Une question importante sera celle de la structure du groupe multiplicatif des corps finis. Ici :
-
- Si p est premier, alors le groupe des inversibles Z/p.Z* est un groupe cyclique d'ordre p - 1.
Cette propriété est démontrée dans le paragraphe Cas où n est premier de l'article Anneau Z/nZ.
On verra plus loin que ces exemples sont en fait les seuls exemples de corps finis de cardinal un nombre premier, mais aussi que tout corps fini peut s'obtenir par extension algébrique à partir d'un tel corps. Si p est un nombre premier, Fp désigne le corps Z/p.Z.
Il existe des polynômes irréductibles P(X) de Fp [X] tel que le quotient Fp [X]/(P(X)) de l'anneau des polynômes Fp [X] par l'idéal principal engendré par un tel polynôme irréductible P(X) soit un corps fini (commutatif). Il contient strictement le corps premier d'ordre p, si le polynôme n'est pas de degré un. Ce corps n'est autre qu'un corps de rupture du polynôme : la classe de X fournit une racine de P. Ici X désigne une indéterminée et P(X) un polynôme formel. L'usage de polynômes formels à la place d'une fonction polynôme est indispensable, il existe des polynômes non-nuls dont les fonctions polynômes associées sont identiquement nulles sur Fp (par exemple X + X2 sur F2). Une autre manière de se rendre compte de la différence est qu'il ne peut exister qu'un nombre fini de fonctions de Fp dans Fp et donc de fonctions polynômes, alors qu'il existe un nombre infini de polynômes formels.
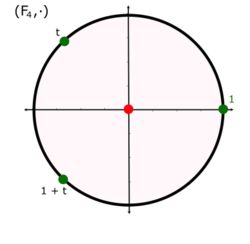
Par exemple, pour p=2, le polynôme 1+X+X2 est irréductible dans F2 [X] (c'est d'ailleurs l'unique polynôme irréductible de degré 2). L'extension correspondante est un corps noté F4. Ce corps a exactement 4 éléments qui sont 0, 1, et les deux racines x et x+1 de 1+X+X2. Ses lois sont données comme suit :
+ 0 1 x x+1 0 0 1 x x+1 1 1 0 x+1 x x x x+1 0 1 x+1 x+1 x 1 0 . 0 1 x x+1 0 0 0 0 0 1 0 1 x x+1 x 0 x x+1 1 x+1 0 x+1 1 x Le groupe multiplicatif des inversibles Fq* est monogène, isomorphe au groupe cyclique Z/(q-1)Z. Dans notre exemple, F4 est engendré par les puissances de la classe de x: x2=x+1, x3=1. La table de multiplication est facile à écrire en termes de ce groupe cyclique, mais c'est alors l'addition qui est moins commode.
Pour p > 2, la fonction polynomiale carrée, qui à x associe son carré x2 n'est pas injective car envoie les éléments distincts 1 et -1 sur 1. Comme son ensemble de départ est égal à son ensemble d'arrivée et est de cardinal fini, la fonction n'est pas non plus surjective. Ainsi, il existe au moins un élément a tel que le polynôme P(X) égal à X2 - a ne soit pas scindé. L'extension associée à ce polynôme est de degré 2 et fournit un corps contenant n = p2 éléments noté Fn. À isomorphisme près, ce corps est indépendant de a.
Extensions de corps finis
Le théorème de Wedderburn montre que tout corps fini est commutatif, il est donc une extension finie d'un corps premier.
On montre d'abord que tout corps fini est de cardinal la puissance d'un nombre premier, puis qu'il existe à isomorphisme près un unique corps fini de tel cardinal donné.
Caractéristique et cardinal
Articles détaillés : Caractéristique d'un anneau et Extension finie.Soit K un corps fini et p sa caractéristique, c'est-à-dire le plus petit entier tel que l'addition de 1 itérée p fois soit égal à 0. Un tel nombre existe car sinon, le groupe additif engendré par 1 serait de cardinal infini et K ne contient pas de sous-ensemble infini. De plus, p est un nombre premier. En effet, si a et b sont des entiers tels que a.b = p, alors le produit de a par b est nul dans K, ce qui montre que soit a soit b est un multiple de p, car il n'existe pas de diviseur de 0 dans un corps. L'unique homomorphisme d'anneaux unitaires de Z dans K induit une injection de Z/p.Z dans K son image est le sous-corps de K formé des éléments du sous-groupe additif engendré par 1. C'est un sous-corps de K contenant p éléments et isomorphe à Z/ pZ, encore noté Fp.
Le corps K hérite donc d'une structure d'espace vectoriel sur Fp. Sa dimension étant nécessairement finie, notons la n, son cardinal est alors pn. Pour résumer :
- Le cardinal d'un corps fini est une puissance d'un nombre premier qui en est sa caractéristique. Plus exactement, tout corps fini est une extension finie d'un corps premier Fp.
Automorphisme de Frobenius
Article détaillé : Automorphisme de Frobenius.On suppose ici donné un corps K fini de caractéristique p, de cardinal q = pk. On peut alors montrer la formule importante suivante :
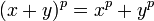
L'application qui, à x, associe xp de K dans lui-même est un endomorphisme bijectif, appelé endomorphisme de Frobenius et est noté ici Frob. Cet automorphisme est important dans l'étude des corps finis. On trouvera le théorème suivant démontré dans l'article dédié :
- Tout corps fini est parfait, c'est-à-dire que ses extensions algébriques sont séparables.
Ce fait a une conséquence importante, par le théorème de l'élément primitif, qui affirme que toute extension finie et séparable est simple c’est-à-dire engendrée par un unique élément :
- Toute extension algébrique de corps finis est simple.
L'étude de l'automorphisme de Frobenius permet aussi de déterminer les polynômes irréductibles sur le corps fini K :
- Les polynômes irréductibles de K de degré n sont les diviseurs premiers de degré n du polynôme suivant et sont donc tous cyclotomiques :
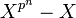
Existence d'un corps fini de cardinal pn
Article détaillé : Corps de décomposition.Soit n un entier strictement positif, q l'entier égal à pn et L le corps de décomposition du polynôme P(X) = Xq - X sur le corps Fp. L'ensemble des éléments invariants par l'automorphisme Frobn est une extension K de Fp. K est exactement l'ensemble des racines de P(X). Or P(X) est scindé sur K, il est de plus séparable car premier avec son polynôme dérivé égal à 1 (cette propriété est démontrée dans le paragraphe Cas des polynômes de l'article Extension séparable). K contient donc autant de racines que son degré, c’est-à-dire pn.
Groupe multiplicatif et conséquences
Soit K un corps fini de cardinal q = pn. Alors, le groupe multiplicatif de ce corps est de cardinal q - 1 ; soit e son exposant, c'est un diviseur de q - 1. Il vient alors que le polynôme Xe - 1 à coefficients dans K, possède q - 1 racines distinctes et est de degré e, ce qui implique que e est supérieur à q - 1, puis l'égalité. L'exposant du groupe multiplicatif étant égal à son ordre, et comme dans un groupe fini commutatif l'exposant est toujours l'ordre d'un élément du groupe, on trouve :
- Le groupe multiplicatif d'un corps fini est cyclique.
En conséquence, tout corps de cardinal q est un corps de décomposition du polynôme Xq - X sur Fp. Deux tels corps de décomposition sont isomorphes, donc si on fixe une clôture algébrique de Fp, alors :
- Il existe un et un seul corps de cardinal q, noté Fq, contenu dans la clôture algébrique fixée.
Propriétés galoisiennes
Article détaillé : Extension de Galois.Une conséquence du paragraphe précédent est que le polynôme minimal ψq-1(X) d'un élément primitif est de degré n, et le corps Fq de cardinal q est isomorphe au corps de rupture Fp[X]/ψq-1(X). Or, ce polynôme est diviseur du polynôme Xq-1-1, qui est scindé dans Fq. Ainsi :
- L'extension Fq/Fp est corps de décomposition du polynôme cyclotomique ψq-1(X). C'est une extension galoisienne.
Et, plus précisément, l'endomorphisme de Frobenius Frob est un automorphisme du corps Fq' laissant son sous-corps premier invariant, c'est donc un élément du groupe de Galois. Considérant ensuite un élément x primitif dans Fq, on voit que :
et, par primitivité, n est la plus petite puissance de Frob laissant x fixe. Frob est donc un élément d'ordre au moins n du groupe de Galois, qui est d'ordre le degré n de l'extension :
- L'endomorphisme de Frobenius est un générateur du groupe de Galois Gal ( Fq/Fp), qui est en particulier cyclique d'ordre n.
Le théorème fondamental de la théorie de Galois permet la détermination des sous-corps d'un corps fini. Les sous-groupes du groupe de Galois sont les groupes cycliques d'ordre un diviseur de n, en conséquence :
- Il existe exactement autant de sous-corps que de diviseurs d de n pour une extension de cardinal pn. Les sous-corps K' ont pour cardinal pd, ce sont des extensions de Galois, et le groupe Gal ( K/K' ) est un groupe cyclique d'ordre n/d.
Clôture algébrique
On connaît par ce qui précède toutes les extensions finies, et donc, par réunion, toutes les extensions algébriques des corps finis. Toute clôture algébrique
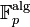 de
de 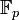 peut être vue comme le compositum des
peut être vue comme le compositum des 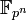 .
.Du point de vue de la théorie de Galois, la famille des groupes
 , pour n variant, forme donc ce qu'on appelle un système projectif, c'est-à-dire que le groupe de Galois absolu
, pour n variant, forme donc ce qu'on appelle un système projectif, c'est-à-dire que le groupe de Galois absolu 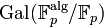 est la limite projective des groupes
est la limite projective des groupes 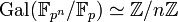 ; c'est donc le complété profini
; c'est donc le complété profini 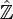 de
de 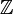 , qui est ainsi un groupe procyclique : un générateur naturel est à nouveau l'endomorphisme de Frobenius, qui peut être vu comme la donnée de la famille compatible des endomorphismes de Frobenius des extensions finies.
, qui est ainsi un groupe procyclique : un générateur naturel est à nouveau l'endomorphisme de Frobenius, qui peut être vu comme la donnée de la famille compatible des endomorphismes de Frobenius des extensions finies.Cette description complète des extensions algébriques des corps finis est un élément important qui intervient dans la théorie des corps de classes pour les corps de nombres et les corps de nombres p-adiques, car leurs corps résiduels sont des corps finis.
Polynôme irréductible
Extension normale et polynôme cyclotomique
Article détaillé : Polynôme cyclotomique.Soit p un nombre premier n un entier strictement positif et K un corps de cardinal q = pn.
Le paragraphe précédent montre que tout élément de K est racine du polynôme Xq - X. À l'exception de l'élément nul, tout élément est racine de l'unité. Cette propriété est illustrée sur la figure de droite, les trois éléments non nuls de F4 sont les trois racines de l'unité. Cette remarque amène la proposition suivante:
- Tout élément de K* est racine de l'unité et tout polynôme irréductible autre que X divise un polynôme cyclotomique.
Si φ désigne la fonction indicatrice d'Euler il existe exactement φ(q - 1) éléments primitifs dans K. Chaque élément primitif possède un polynôme minimal à coefficients dans Fp de degré n égal à la dimension de K considéré comme espace vectoriel sur Fp.
- Le nombre Nm de polynômes irréductibles unitaires de degré m à coefficients dans K est égal à, si μ désigne la fonction de Möbius :
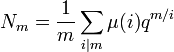
La démonstration est proposée dans l'article Fonction de Möbius.
- Il existe exactement φ(q - 1) éléments primitifs dans K, correspondant à φ(q - 1)/n polynômes sur Fp.
Cependant, il peut y avoir d'autres polynômes irréductibles de même degré: dans F9, on a x8 - 1 = (x - 1)(x + 1)(x2 + 1)(x2 + x +2)(x2 + 2x + 2), x2 + 1, bien qu'irréductible, n'étant le polynôme minimal d'aucun des 4 éléments primitifs.
Cette propriété est associée à une définition dans la théorie des corps finis:
- Deux éléments de K sont dits conjugués si et seulement s'ils possèdent le même polynôme irréductible. La relation de conjugaison est une classe d'équivalence. Chaque classe possède comme cardinal le degré du polynôme irréductible associé.
Deux propriétés supplémentaires indiquent la relation entre les polynômes cyclotomiques et leur degré dans le cas de la caractéristique p. Elles sont démontrées dans l'article associé.
- Un diviseur du polynôme cyclotomique d'indice q - 1 sur Fp est de degré l'ordre multiplicatif de p modulo q - 1.
- Le produit des polynômes irréductibles de degré n est le polynôme cyclotomique d'indice q - 1.
Caractéristique deux
Il existe exactement deux polynômes unitaires de degré un et le deuxième est le polynôme cyclotomique d'indice un:
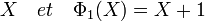
Il existe exactement un polynôme de degré deux irréductible, il est primitif, c'est le polynôme cyclotomique d'indice trois. Il est scindé dans F4 et l'on reconnaît le polynôme cyclotomique d'indice 3 dans Z:
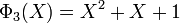
Il existe exactement deux polynômes de degré trois irréductibles car le corps contient six éléments hors de son unique sous-corps. Le groupe multiplicatif contient sept éléments, donc six sont générateurs. Il existe donc deux polynômes primitifs ce sont les deux polynômes cyclotomiques d'indice sept, scindé dans F8:
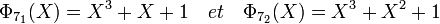
Leur produit est bien l'image du polynôme cyclotomique à coefficients dans Z:
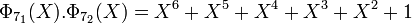
Le corps F16 contient deux sous-corps F4 et F2. En conséquence, il existe exactement trois polynômes irréductibles de degré quatre. Le groupe multiplicatif F16* contient huit générateurs car l'indicatrice d'Euler appliqué à quinze est égal à huit, il existe donc deux polynômes de racines des éléments primitifs. Le polynôme restant est celui correspondant au polynôme cyclotomique d'indice cinq. Il existe donc deux polynômes cyclotomiques d'indice quinze et un polynôme cyclotomique d'indice cinq.
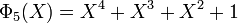
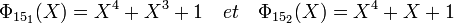
Une fois encore, le produit des deux polynômes cyclotomiques d'indice 15 est bien l'image du polynôme cyclotomique à coefficients dans Z:
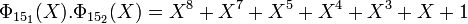
Caractéristique trois
Il existe trois polynômes unitaires de degré un, le deuxième est le polynôme cyclotomique d'indice un et le troisième d'indice deux.
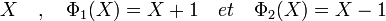
L'extension d'ordre neuf contient six éléments hors du corps premier, elle est de dimension deux, il existe donc exactement trois polynômes irréductibles. Le groupe multiplicatif est d'ordre huit et contient quatre éléments générateurs, deux des polynômes sont donc cyclotomiques d'ordre huit, le dernier est cyclotomique d'ordre quatre.
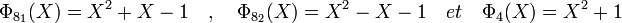
L'extension d'ordre vingt-sept contient un unique sous-corps le corps premier. Il existe donc vingt-quatre éléments hors de tout sous-corps et huit polynômes irréductibles de degré trois. Le groupe multiplicatif contient vingt-six éléments et douze générateurs et il existe quatre polynômes cyclotomiques d'indice vingt-six et quatre d'indice treize.
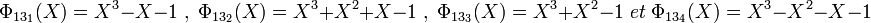
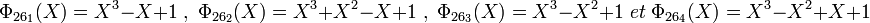
On vérifie de même que :
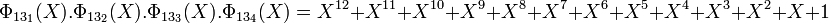
Applications
Équation diophantienne
Article détaillé : Théorème des deux carrés de Fermat.Une équation diophantienne est une équation à coefficients entiers où des solutions entières sont recherchées. Pierre de Fermat (1601, 1665) s'est longuement penché sur des équations de cette nature.
Le petit théorème de Fermat stipule que, si p est premier, alors tout entier à la puissance p est congru modulo p à cet entier. Dans le contexte des corps finis, cela revient à indiquer que les points fixes de l'automorphisme de Frobenius sont les éléments du corps premier, ou que le groupe multiplicatif de ce dernier est cyclique d'ordre p - 1.
Fermat remarque que les seuls nombres premiers, somme de deux carrés, sont ceux dont la division par quatre donne un pour reste. Il remarque en effet que:
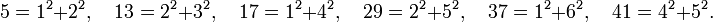
Il propose l'équation suivante a 2 + b 2 = p avec p premier dans une lettre écrite à Marin Mersenne, datée du 25 décembre 1640.
Richard Dedekind (1831-1916) propose une démonstration[15] dont la première partie consiste à étudier l'équation sur le corps Fp. Il utilise les propriétés du groupe multiplicatif et celles des polynômes à coefficients dans un corps. L'équation devient a 2 + b 2 = 0. Si b est égal à 0 alors a l'est aussi et la solution est triviale. Dans le cas contraire. Il est possible de diviser par b car la structure sous-jacente est celle d'un corps, l'équation devient alors X 2 + 1 = 0. En multipliant le polynôme précédent par X 2 - 1 = 0, il obtient l'équation suivante : X 4 - 1 = 0. Les propriétés du groupe multiplicatif donne une condition nécessaire et suffisante sur p, il doit être congru à un modulo quatre. La fin de la démonstration n'utilise pas les corps finis, elle est donnée dans l'article associé.
Cette méthode, consistant à réduire l'équation dans le corps premier est fréquente. Le corps dispose d'une structure plus forte et de nombreux théorèmes pour conclure.
Code correcteur
Les codes correcteurs ont leur source dans un problème très concret lié à la transmission de données. Dans certains cas, une transmission de données se fait en utilisant une voie de communication qui n'est pas entièrement fiable. Autrement dit, les données, lorsqu'elles circulent sur cette voie, sont susceptible d'être altérées. L'objectif d'un code correcteur est l'apport d'une redondance de l'information de telle manière à ce que l'erreur puisse être détectée et même corrigée.
Un message est une suite finie de lettres, qui dans le cas d'un code linéaire sont considérées comme des éléments d'un corps fini. Un message m apparaît comme un élément d'un espace vectoriel E sur un corps fini de dimension k. L'apport de la redondance est le résultat d'une application linéaire injective φ de E dans un espace F appelé code et de dimension n supérieur à k. Le mot du code transmis est l'élément φ(m). L'intérêt de transmettre φ(m) à la place de m est illustré par la figure suivante :
Si le message m est transmis, et si la transmission l'altère, alors le message reçu est erroné (comme illustré sur la figure de gauche) et le récepteur ne dispose d'aucun moyen pour repérer ou corriger l'erreur. Si l'application φ est astucieusement choisie, chaque point du code diffère des autres points du code par au moins d coordonnées. Cette situation est illustrée sur la figure de droite. Les points du code sont illustrés en vert, la modification d'une coordonnée est symbolisée par un segment du quadrillage. On remarque sur la figure que les points du code diffèrent tous par au moins d = 3 coordonnées. Si, par exemple, l'altération porte sur une unique coordonnée, la transmission correspond à un point rouge. Le récepteur peut alors corriger l'erreur, car il n'existe qu'un seul point du code (en vert) à une distance de 1 du message reçu.
L'application qui, à deux points de F, associe le nombre de coordonnées distinctes est une distance au sens mathématique, appelée distance de Hamming. Si la distance de Hamming minimale entre deux points du code est égale à d, alors le code est à même de corriger t altérations où t est le plus grand entier strictement plus petit que d/2. Sur la figure ci-dessus, on remarque des points noirs. Ils correspondent à des redondances inutiles. Ils sont en effet à une distance de deux des points du code, or une telle distance n'est pas traitable dans le cas de la figure.
L'ensemble des points corrigeables est donné par la réunion de toutes les boules de centre un point du code et de rayon t. La configuration idéale est celle où ces boules forment une partition de F. Il n'existe alors aucune redondance inutile. Cette situation est illustrée par la figure de droite. Les points du code sont illustrés en vert, la distance minimale d est égale à 5. Les boules de centre les points du code et de rayon 2 forment une partition de F. Les points à distance 1 du code sont illustrés en bleu, ceux à distance 2 en rouge. Tout message contenant au plus deux altérations peut être corrigé. Un tel code est dit parfait.
La théorie des corps finis permet de construire des codes parfaits. L'espace F est muni de la structure d'anneau Fd[X]/P(X) où P(X) = Xn - 1 avec n = d a - 1 et a est un entier strictement positif. F correspond à l'ensemble des polynômes prenant des valeurs distinctes sur le corps Fn+1. Si φ(E) est l'idéal engendré par le polynôme G(X) à coefficients dans Fd ayant pour racines α, α2, ..., αd-1, alors le code est de distance minimale d. G(X) est le produit de polynômes cyclotomiques. Le code BCH ou le code de Reed-Solomon utilise cette technique pour construire des codes parfaits. Si k est l'entier tel que n - k est égal au degré de G(X), alors l'application φ associe au message M(X) le polynôme M(X).Xk - R(X) où R(X) est le reste de la division euclidienne de M(X).Xk par G(X). Les détails et démonstrations sont donnés dans l'article code cyclique.
Géométrie arithmétique
Notes et références
Notes
- ↑ N. Bourbaki Algèbre commutative. Chapitre 5 Hermann 1964
- ↑ Richard Dedekind, Lechbuch des Algebra 1871.
- ↑ Heinrich Weber, Lechbuch der Algebra 1895.
- ↑ Ferdinand Georg Frobenius, Sur le caractère du groupe, Académie de Berlin, 1896
- ↑ Leonard Dickson, Linear Groups With an Exposition of the Galois Field Theory, 1901
- ↑ Carl Friedrich Gauss, Disquisitiones Arithmeticae, 1801.
- ↑ Claude Shannon A mathematical theory of communication Bell System Technical Journal, vol. 27, pp. 379-423 et 623-656, Juil et Oct 1948
- ↑ Claude Shannon Communication Theory of Secrecy Systems Bell System Technical Journal, Vol 28, pp. 656-715, Oct 1949
- ↑ Michael Rabin, Probabilistic Algorithm for Testing Primality J. Number Th. 12, 128-138, 1980
- ↑ Richard Hamming Error-detecting and error-correcting codes Bell Syst. Tech. J. 29 pp 147 à 160 1950
- ↑ R. C. Bose and D. K. Ray-Chaudhuri On a class of error-. correcting. binary group codes Inform. Control, vol. 3, pp. 68-79, Mars 1960
- ↑ A. Hocquenghem Codes correcteurs d'erreurs Chiffre 1959
- ↑ I. Reed G. Solomon Polynomial codes over certain finite fields J. Soc. Indus. Appl Math Vol 8 n° 2 pp 300 à 304 1960
- ↑ V.D. Goppa Codes associated with divisors Problems of Information Transmission, 12(1):22--27, 1977
- ↑ Richard Dedekind Supplément XI des Leçons en théorie des nombres de Dirichlet 1894
Liens externes
- (fr) Codes géométriques et algébrique et arithmétique sur les corps finis par le Centre de Mathématiques de l'École Polytechnique
- (en) Une histoire des mathématiques Université de Saint Andrew
- (fr) Corps finis par David A. Madore
- (fr) Factorisation de polynômes sur les corps finis par David A. Madore
- (fr) Corps finis par les-mathematiques.net
Références
- N. Bourbaki Algèbre commutative. Chapitre 5 Hermann 1964
- Pierre Samuel, Théorie algébrique des nombres [détail des éditions]
- Jean-Pierre Serre, Cours d'arithmétique [détail des éditions]
- G. Heuzé Sur les corps finis Mathématiques et Sciences Humaines 1974
- A. Warusfel Structures algébriques finies Hachette Université 1971
- Portail des mathématiques
Catégories : Bon article | Corps fini -
Wikimedia Foundation. 2010.