- Corps Ordonné
-
Corps ordonné
En algèbre générale, un corps ordonné est la donnée d'un corps
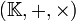 , muni d'une relation d'ordre (notée
, muni d'une relation d'ordre (notée 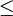 dans l'article) compatible avec la structure de corps.
dans l'article) compatible avec la structure de corps.Dans tout l'article, on note naturellement
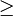 la relation d'ordre réciproque de
la relation d'ordre réciproque de 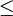 , et l'on note < et > les relations d'ordre strict respectivement associées à
, et l'on note < et > les relations d'ordre strict respectivement associées à 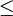 et
et 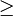 . On note par ailleurs 0 l'élément neutre de l'addition et 1 celui de la multiplication. Enfin, on note x − 1 l'inverse d'un élément x non nul de
. On note par ailleurs 0 l'élément neutre de l'addition et 1 celui de la multiplication. Enfin, on note x − 1 l'inverse d'un élément x non nul de 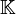 .
.La majeure partie des résultats énoncés (ceux ne faisant pas intervenir la notion d'inverse) peut s'étendre aux anneaux.
Sommaire
Définitions
Plus précisément, avec les notations précédentes, on dit que la relation d'ordre
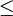 est compatible avec la structure de corps de
est compatible avec la structure de corps de 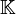 si les deux conditions suivantes sont réunies.
si les deux conditions suivantes sont réunies.- Le groupe additif
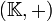 est un groupe ordonné par la relation d'ordre
est un groupe ordonné par la relation d'ordre 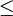 (c'est-à-dire que celle-ci est compatible avec l'addition).
(c'est-à-dire que celle-ci est compatible avec l'addition). - On a, pour tous éléments x et y du corps tels que
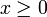 et
et 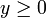 , l'inégalité
, l'inégalité 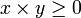 (la relation d'ordre est compatible avec la multiplication).
(la relation d'ordre est compatible avec la multiplication).
Par commodité, on dira par la suite qu'un élément x de
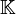 est positif si l'on a
est positif si l'on a 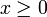 , et qu'il est négatif si l'on a
, et qu'il est négatif si l'on a 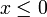 (on remarquera, par antisymétrie de la relation d'ordre
(on remarquera, par antisymétrie de la relation d'ordre 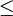 , que 0 est l'unique élément du corps à la fois positif et négatif).
, que 0 est l'unique élément du corps à la fois positif et négatif).Exemples
Les corps
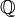 des rationnels et
des rationnels et  des réels, munis de la relation d'ordre habituelle, sont des corps ordonnés.
des réels, munis de la relation d'ordre habituelle, sont des corps ordonnés.Propriétés
On dispose d'abord des propriétés liées à la compatibilité de l'addition avec la relation d'ordre (voir l'article groupe ordonné pour leur démonstration, avec d'autres notations).
- Addition membre à membre d'inégalités. Pour tous éléments x, y, x' et y' de
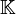 tels que
tels que 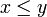 et
et  , on a
, on a  .
. - Passage à l'opposé dans une inégalité en en changeant le sens. Pour tous éléments x et y tels que
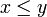 , on a
, on a 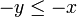 .
.
On dispose par ailleurs de propriétés liées à la compatibilité de la multiplication avec la relation d'ordre.
- Règle des signes.
- Pour tous éléments x et y de
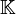 tels que
tels que 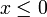 et
et  , on a l'inégalité
, on a l'inégalité 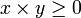 .
. - Pour tous éléments x et y de
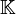 tels que
tels que 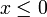 et
et 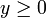 , on a l'inégalité
, on a l'inégalité 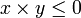 .
. - Pour tous éléments x et y de
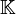 tels que
tels que 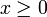 et
et  , on a l'inégalité
, on a l'inégalité 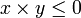 .
.
- Pour tous éléments x et y de
Cela se déduit aisément du deuxième axiome de la définition de la compatibilité, en utilisant le fait qu'un élément négatif est l'opposé d'un élément positif, et que l'opposé d'un élément est obtenu en le multipliant (à gauche ou à droite) par l'opposé de l'unité 1.
- Si 0 et 1 sont comparables, on a nécessairement
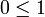 .
.
En effet, on a
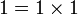 , et si 0 et 1 sont comparables, on a soit
, et si 0 et 1 sont comparables, on a soit 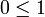 , soit
, soit 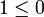 , mais la règle des signes permet d'éliminer la seconde possibilité.
, mais la règle des signes permet d'éliminer la seconde possibilité.- Multiplication membre à membre d'inégalités entre éléments positifs. Pour tous éléments
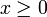 , y,
, y, 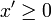 et y' de
et y' de 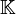 tels que
tels que 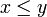 et
et  , on a
, on a 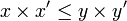 .
.
Démonstration. Les hypothèses se traduisent par les inégalités
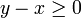 et
et 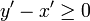 et il s'agit de prouver l'inégalité
et il s'agit de prouver l'inégalité 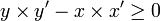 . Il suffit pour y parvenir d'utiliser la décomposition
. Il suffit pour y parvenir d'utiliser la décomposition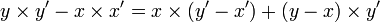 ,
,le membre de droite de cette inégalité étant positif en tant que somme de deux produits d'éléments positifs (la positivité de y' découlant de celle de x' et de la transitivité de la relation d'ordre
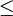 ).
). 
On remarquera que l'hypothèse peut être affaiblie en permettant à l'un des éléments x, x', y et y' d'être strictement négatif, mais pas plus. Par exemple, dans le corps des rationnels, on a
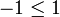 et
et 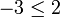 , mais on a
, mais on a 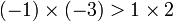 .
.- Passage à l'inverse dans une inégalité entre éléments strictement positifs, en en changeant le sens. Pour tous éléments x > 0 et y de
 tels que x − 1 > 0, y − 1 > 0 et
tels que x − 1 > 0, y − 1 > 0 et 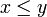 , on a
, on a 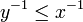 .
.
Pour le prouver, il suffit d'appliquer la règle de multiplication membre à membre aux trois inégalités
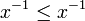 ,
, 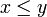 et
et 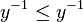 (dans cet ordre). On remarquera que si la relation d'ordre est totale, les hypothèses x − 1 > 0 et y − 1 > 0 sont superflues.
(dans cet ordre). On remarquera que si la relation d'ordre est totale, les hypothèses x − 1 > 0 et y − 1 > 0 sont superflues.Corps totalement ordonné
On appelle corps totalement ordonné un corps ordonné pour lequel la relation d'ordre est totale. Par exemple, les corps
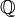 des rationnels et
des rationnels et  des réels, munis de la relation d'ordre habituelle, sont des corps totalement ordonnés.
des réels, munis de la relation d'ordre habituelle, sont des corps totalement ordonnés.En revanche, le corps
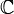 des nombres complexes ne peut pas être muni d'une structure de corps totalement ordonné.
des nombres complexes ne peut pas être muni d'une structure de corps totalement ordonné.Démonstration. On raisonne par l'absurde en supposant que
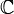 est muni d'une relation d'ordre compatible avec sa structure de corps, et le rendant totalement ordonné. On note
est muni d'une relation d'ordre compatible avec sa structure de corps, et le rendant totalement ordonné. On note 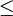 cette relation (on prendra cependant garde à ce qu'elle n'a a priori aucune raison de coïncider avec la relation d'ordre usuelle par restriction aux nombres réels). On note i l'un des deux nombres complexes de carré égal à − 1. Comme l'ordre est total, d'après la règle des signes et l'égalité i2 = − 1, on obtiendrait l'inégalité
cette relation (on prendra cependant garde à ce qu'elle n'a a priori aucune raison de coïncider avec la relation d'ordre usuelle par restriction aux nombres réels). On note i l'un des deux nombres complexes de carré égal à − 1. Comme l'ordre est total, d'après la règle des signes et l'égalité i2 = − 1, on obtiendrait l'inégalité  . Cela entraînerait, par passage à l'opposé, l'inégalité
. Cela entraînerait, par passage à l'opposé, l'inégalité 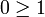 . Mais comme 0 et 1 sont comparables, on a nécessairement
. Mais comme 0 et 1 sont comparables, on a nécessairement 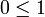 , et l'on obtiendrait l'égalité 0 = 1, ce qui est une contradiction. Par conséquent, la relation d'ordre ne peut pas être à la fois totale et compatible avec la structure de corps de
, et l'on obtiendrait l'égalité 0 = 1, ce qui est une contradiction. Par conséquent, la relation d'ordre ne peut pas être à la fois totale et compatible avec la structure de corps de  .
. 
Remarque. Il est en revanche aisé de définir sur
 une relation d'ordre qui est soit totale, soit compatible avec sa structure de corps.
une relation d'ordre qui est soit totale, soit compatible avec sa structure de corps.- Exemple 1. La relation d'ordre lexicographique
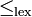 , définie par
, définie par
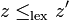 si, en notant z = x + iy et z' = x' + iy', avec x, y, x' et y' réels, on a soit x < x', soit x = x' et
si, en notant z = x + iy et z' = x' + iy', avec x, y, x' et y' réels, on a soit x < x', soit x = x' et  ,
,(les réels étant comparés par la relation d'ordre usuelle) est totale mais n'est pas compatible avec la structure de corps. Sa totalité se déduit aisément de celle de la relation d'ordre usuelle sur les réels. Mais on a
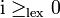 et i2 = − 1 < lex0, ce qui contredit la règle des signes.
et i2 = − 1 < lex0, ce qui contredit la règle des signes.- Exemple 2. La relation d'ordre de comparaison des parties réelles
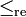 , définie par
, définie par
 si, en notant z = x + iy et z' = x' + iy', avec x, y, x' et y' réels, on a
si, en notant z = x + iy et z' = x' + iy', avec x, y, x' et y' réels, on a 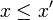 et y = y',
et y = y',est compatible avec la structure de corps (car l'ordre sur les réels l'est), mais n'est pas totale. En particulier, les nombres 0 et i ne sont pas comparables pour cette relation.
Voir aussi
- Portail des mathématiques
Catégories : Théorie des ordres | Structure algébrique - Le groupe additif
Wikimedia Foundation. 2010.
