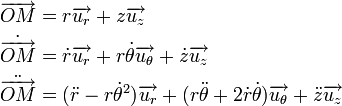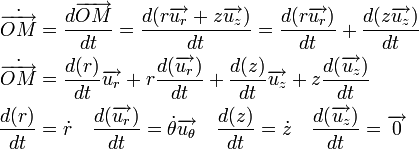Coordonnees cylindriques
- Coordonnees cylindriques
-
Coordonnées cylindriques
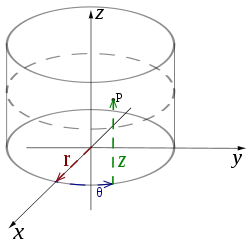
Un point repéré en coordonnées cylindriques
Le système de coordonnées cylindriques est un système de coordonnées qui étend le système de coordonnées polaires à deux dimensions en y ajoutant une troisième dimension qui mesure la hauteur d'un point par rapport au plan repéré par les coordonnées polaires; de la même manière que l'on étend le système de coordonnées cartésiennes de deux à trois dimensions. La troisième coordonnée est souvent notée h ou z.
Les trois coordonnées cylindriques peuvent être converties en coordonnées cartésiennes par:
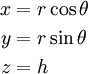
![\begin{align}
\\
\theta\in[0,2\pi]
\end{align}](/pictures/frwiki/97/acd54965f99999c9aa92ad2fb1bf7fe4.png)
Cinématique
Pour 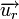 un vecteur radial et
un vecteur radial et 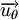 un vecteur orthoradial, les quantités cinématiques, position, vitesse et accélération sont données par :
un vecteur orthoradial, les quantités cinématiques, position, vitesse et accélération sont données par :
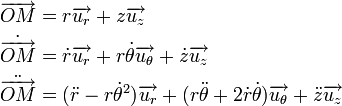
Il est à noter que l'on peut retrouver ces résultats :
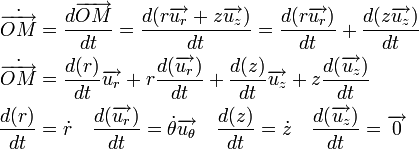
On retrouve donc l'expression de 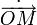
 Portail de la géométrie
Portail de la géométrie
Catégorie : Système de coordonnées
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Coordonnees cylindriques de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Coordonnées Cylindriques — Un point repéré en coordonnées cylindriques Le système de coordonnées cylindriques est un système de coordonnées qui étend le système de coordonnées polaires à deux dimensions en y ajoutant une troisième dimension qui mesure la hauteur d un point … Wikipédia en Français
Coordonnées cylindriques — En coordonnées cylindriques, la position du point P est définie par les distances r et Z et par l angle θ. Le système de coordonnées cylindriques est un système de coordonnées qui étend le système de coordonnées polaires à deux dimensions en y… … Wikipédia en Français
coordonnées cylindriques — cilindrinės koordinatės statusas T sritis automatika atitikmenys: angl. cylindrical coordinates vok. zylindrische Koordinaten, f rus. цилиндрические координаты, f pranc. coordonnées cylindriques, f … Automatikos terminų žodynas
coordonnées cylindriques — cilindrinės koordinatės statusas T sritis fizika atitikmenys: angl. cylindrical coordinates vok. zylindrische Koordinaten, f rus. цилиндрические координаты, f pranc. coordonnées cylindriques, f … Fizikos terminų žodynas
Système de coordonnées cylindriques — Coordonnées polaires Un cercle découpé en angles mesurés en degré Les coordonnées polaires sont, en mathématiques, un système de coordonnées à deux dimensions, dans lequel chaque point du plan est entièrement déterminé par un angle et une… … Wikipédia en Français
Opérateurs nabla dans les coordonnées cylindriques et sphériques — Nabla Articles d analyse vectorielle Objets d étude … Wikipédia en Français
système de coordonnées cylindriques — cilindrinė koordinačių sistema statusas T sritis fizika atitikmenys: angl. cylindrical co ordinates system vok. Zylinderkoordinatensystem, n rus. цилиндрическая система координат, f pranc. système de coordonnées cylindriques, m … Fizikos terminų žodynas
Coordonnees polaires — Coordonnées polaires Un cercle découpé en angles mesurés en degré Les coordonnées polaires sont, en mathématiques, un système de coordonnées à deux dimensions, dans lequel chaque point du plan est entièrement déterminé par un angle et une… … Wikipédia en Français
Coordonnées Polaires — Un cercle découpé en angles mesurés en degré Les coordonnées polaires sont, en mathématiques, un système de coordonnées à deux dimensions, dans lequel chaque point du plan est entièrement déterminé par un angle et une distance. Ce système est… … Wikipédia en Français
Coordonnées polaires (Mathématiques) — Coordonnées polaires Un cercle découpé en angles mesurés en degré Les coordonnées polaires sont, en mathématiques, un système de coordonnées à deux dimensions, dans lequel chaque point du plan est entièrement déterminé par un angle et une… … Wikipédia en Français
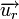 un vecteur radial et
un vecteur radial et 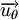 un vecteur orthoradial, les quantités cinématiques, position, vitesse et accélération sont données par :
un vecteur orthoradial, les quantités cinématiques, position, vitesse et accélération sont données par :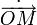


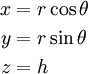
![\begin{align}
\\
\theta\in[0,2\pi]
\end{align}](/pictures/frwiki/97/acd54965f99999c9aa92ad2fb1bf7fe4.png)