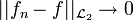Convergence Quadratique
- Convergence Quadratique
-
Convergence quadratique
La convergence quadratique d'une fonction f est une forme de convergence en moyenne, différente toutefois de cette dernière, plus faible par ailleurs que la convergence uniforme. La convergence quadratique n'implique en général pas la convergence simple.
Définition
On dit qu'une suite de fonction fn converge quadratiquement vers f si et seulement si 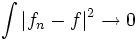
Cette convergence est aussi appelée convergence en norme 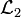 . On peut aussi écrire cette définition comme
. On peut aussi écrire cette définition comme 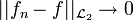
Voir aussi
 Portail des mathématiques
Portail des mathématiques
Catégories : Analyse fonctionnelle | Analyse réelle
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Convergence Quadratique de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Convergence quadratique — Ne pas confondre avec la convergence en moyenne quadratique des suites de fonctions. En mathématiques, la convergence quadratique d une suite est une vitesse de convergence d exposant 2, c est à dire que la précision de l approximation… … Wikipédia en Français
Convergence en moyenne quadratique — Ne pas confondre avec la convergence quadratique d une suite numérique. Expression de la distance L2 entre deux fonctions numériques sur un même espace mesuré. La convergence en moyenne quadratique d une suite de fonctions … Wikipédia en Français
Quadratique — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Quadratique », sur le Wiktionnaire (dictionnaire universel) Le terme de quadratique recouvre plusieurs … Wikipédia en Français
Convergence De Variables Aléatoires — Dans la théorie des probabilités, il existe différentes notions de convergence de variables aléatoires. La convergence (dans un des sens décrits ci dessous) de suites de variables aléatoires est un concept important de la théorie des probabilités … Wikipédia en Français
Convergence de variables aleatoires — Convergence de variables aléatoires Dans la théorie des probabilités, il existe différentes notions de convergence de variables aléatoires. La convergence (dans un des sens décrits ci dessous) de suites de variables aléatoires est un concept… … Wikipédia en Français
Convergence de variables aléatoires — Dans la théorie des probabilités, il existe différentes notions de convergence de variables aléatoires. La convergence (dans un des sens décrits ci dessous) de suites de variables aléatoires est un concept important de la théorie des probabilités … Wikipédia en Français
Convergence linéaire — Vitesse de convergence En analyse numérique, la vitesse de convergence d une suite représente la vitesse à laquelle les termes de la suite se rapprochent de sa limite. Bien que cet ordre de grandeur de vitesse de convergence ne fournisse pas d… … Wikipédia en Français
Vitesse de convergence des suites — En analyse numérique, qui est une branche des mathématiques, on peut classer les suites convergentes en fonction de leur vitesse de convergence vers leur point limite. C est une manière d apprécier l efficacité des algorithmes qui les génèrent.… … Wikipédia en Français
Erreur Quadratique Moyenne — En statistiques, l’erreur quadratique moyenne (ou plus souvent l’erreur quadratique, moyenne étant sous entendu) pour un paramètre θ de dimension 1, que nous noterons MSE (pour Mean Squared Error), est définie par: Définition ave … Wikipédia en Français
Erreur moyenne quadratique — Erreur quadratique moyenne En statistiques, l’erreur quadratique moyenne (ou plus souvent l’erreur quadratique, moyenne étant sous entendu) pour un paramètre θ de dimension 1, que nous noterons MSE (pour Mean Squared Error), est définie par:… … Wikipédia en Français
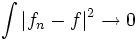
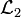 . On peut aussi écrire cette définition comme
. On peut aussi écrire cette définition comme