Connexion (Mathématiques)
- Connexion (Mathématiques)
-
Connexion (mathématiques)

Transport parallèle sur une sphère
En géométrie différentielle, la connexion est un outil pour réaliser le transport parallèle. La notion a été introduite par par Charles Ehresmann et Jean-Louis Koszul en 1951. Il existe plusieurs présentations qui dépendent de l'utilisation faite.
Connexion de Koszul
La connexion de Koszul est un opérateur sur des espaces de sections. Elle a été introduite en 1951 par Koszul pour les fibrés vectoriels, et utilisée par Nomizu en 1954[1].
Une connexion de Koszul est une association à toute section globale s d'un fibré vectoriel E de base B, et à tout champ vectoriel sur B, d'une section globale notée 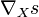 vérifiant :
vérifiant :
- L'application
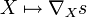 soit
soit 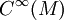 -linéaire ; autrement dit, pour toute fonction régulière f, on a :
-linéaire ; autrement dit, pour toute fonction régulière f, on a :
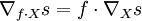 .
.
- De plus,
 doit vérifier la relation de Leibniz :
doit vérifier la relation de Leibniz :
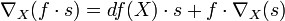 .
.
La relation de Leibniz démontre que la valeur de 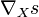 en un point b de B ne dépend que des variations de s au voisinage de b. La
en un point b de B ne dépend que des variations de s au voisinage de b. La 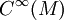 -linéarité implique que cette valeur ne dépend que de X(p).
-linéarité implique que cette valeur ne dépend que de X(p).
Connexion d'Ehresmann
Connexion de Levi-Civita
Voir aussi
Notes et références
Notes
- ↑ Katsumi Nomizu, Invariant affine connections on homogeneous spaces, Amer. J. Math. 76 (1954), pp. 33-65.
Références
- (en) Marcel Berger, A Panoramic View of Riemannian Geometry [détail des éditions]
- Sylvestre Gallot, Dominique Hulin, Jacques Lafontaine ; Riemannian Geometry [détail des éditions]
 Portail de la géométrie
Portail de la géométrie
Catégorie : Géométrie différentielle
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Connexion (Mathématiques) de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Connexion (mathematiques) — Connexion (mathématiques) Transport parallèle sur une sphère En géométrie différentielle, la connexion est un outil pour réaliser le transport parallèle. La notion a été introduite par par Charles Ehresmann et Jean Louis Koszul en 1951. Il existe … Wikipédia en Français
Connexion (mathématiques) — Transport parallèle sur une sphère En géométrie différentielle, la connexion est un outil pour réaliser le transport parallèle. Il existe plusieurs présentations qui dépendent de l utilisation faite. Cette notion a été développée au début des… … Wikipédia en Français
Mathematiques de la relativite generale — Mathématiques de la relativité générale Les mathématiques de la relativité générale se réfèrent à différentes structures et techniques mathématiques utilisées par la théorie de la relativité générale d Albert Einstein. Les principaux outils… … Wikipédia en Français
Mathématiques De La Relativité Générale — Les mathématiques de la relativité générale se réfèrent à différentes structures et techniques mathématiques utilisées par la théorie de la relativité générale d Albert Einstein. Les principaux outils utilisés dans cette théorie géométrique de la … Wikipédia en Français
Connexion De Koszul — En géométrie différentielle, une connexion (de Koszul) est un opérateur sur les sections d un fibré vectoriel. Cette notion a été introduite par Koszul en 1950[réf. nécessaire] et formalise le transport parallèle de vecteurs le long d une… … Wikipédia en Français
Connexion de koszul — En géométrie différentielle, une connexion (de Koszul) est un opérateur sur les sections d un fibré vectoriel. Cette notion a été introduite par Koszul en 1950[réf. nécessaire] et formalise le transport parallèle de vecteurs le long d une… … Wikipédia en Français
Mathématiques de la relativité générale — Les mathématiques de la relativité générale se réfèrent à différentes structures et techniques mathématiques utilisées par la théorie de la relativité générale d Albert Einstein. Les principaux outils utilisés dans cette théorie géométrique de la … Wikipédia en Français
Connexion affine — Une connexion affine sur la sphère fait rouler le plan affine tangent d un point à un autre. Dans ce déplacement, le point de contact trace une courbe du plan : le développement. En mathématiques, et plus précisément en géométrie… … Wikipédia en Français
Connexion de Koszul — En géométrie différentielle, une connexion (de Koszul) est un opérateur sur les sections d un fibré vectoriel. Cette notion a été introduite par Koszul en 1950[réf. nécessaire] et formalise le transport parallèle de vecteurs le long d une… … Wikipédia en Français
Connexion — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Connexion », sur le Wiktionnaire (dictionnaire universel) D une manière générale, une connexion est l… … Wikipédia en Français
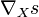 vérifiant :
vérifiant :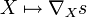 soit
soit 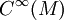 -linéaire ; autrement dit, pour toute fonction régulière f, on a :
-linéaire ; autrement dit, pour toute fonction régulière f, on a :
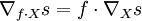 .
. doit vérifier la relation de Leibniz :
doit vérifier la relation de Leibniz :
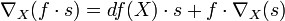 .
.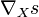 en un point b de B ne dépend que des variations de s au voisinage de b. La
en un point b de B ne dépend que des variations de s au voisinage de b. La 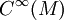 -linéarité implique que cette valeur ne dépend que de X(p).
-linéarité implique que cette valeur ne dépend que de X(p).
