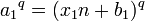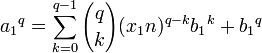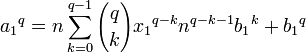- Congruence Sur Les Entiers
-
Congruence sur les entiers
 Pour les articles homonymes, voir Congruence.
Pour les articles homonymes, voir Congruence.La congruence sur les entiers est une relation pouvant unir deux entiers. Elle fut pour la première fois étudiée en tant que structure par le mathématicien allemand Carl Friedrich Gauss à la fin du XVIIIe siècle et présentée au public dans ses Disquisitiones arithmeticae en 1801. Elle est aujourd'hui couramment utilisée en théorie des nombres, en algèbre générale et en cryptographie. Elle représente le fondement d'une branche mathématique appelée arithmétique modulaire.
C'est une arithmétique où l'on ne raisonne pas directement sur les nombres mais sur leurs restes respectifs par la division euclidienne par un certain entier : le modulo (qui sera noté n tout au long de l'article). On parle alors de congruence.
L'histoire, les outils développés pour l'arithmétique modulaire ainsi que les applications sont traités dans l'article Arithmétique modulaire. Une analyse plus exhaustive et moins didactique est proposée dans l'article Anneau Z/nZ.
Sommaire
Idée intuitive : « arithmétique de l'horloge »
L'arithmétique modulaire est un système arithmétique d'entiers modifiés, où les nombres sont « abaissés » lorsqu'ils atteignent une certaine valeur.
Donnons comme exemple, l'« arithmétique de l'horloge » qui se réfère à l'« addition » des heures indiquées par la petite aiguille d'une horloge : concrètement, si nous commençons à 7 heures et ajoutons 8 heures, alors plutôt que de terminer à 15 heures (comme dans l'addition normale), nous sommes à 3 heures. De la même manière, si nous commençons à minuit et nous attendons 7 heures trois fois de suite, nous nous retrouvons à 9 heures (au lieu de 21).
Fondamentalement, quand nous atteignons 12, nous recommençons à zéro ; nous travaillons modulo 12. Pour reprendre l'exemple précédent, on dit que 9 et 21 sont congrus modulo 12. Les nombres 9 ; 21 ; 33 ; 45 ; etc. sont considérés comme égaux lorsqu'on travaille modulo 12.
Pour généraliser, nous pouvons facilement imaginer une horloge qui contient un nombre arbitraire d'heures, et faire des calculs avec un nouveau modulo.
Congruence modulo n
Définition
Deux entiers a et b sont dits congruents modulo n, où n est un entier supérieur ou égal à 2, si l'une des conditions équivalentes suivantes est vérifiée :
- leur différence est divisible par n ; (il existe un entier k tel que a − b = kn )
- le reste de la division euclidienne de a par n est égal à celui de la division de b par n ;
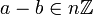 , l'idéal de tous les entiers divisibles par n.
, l'idéal de tous les entiers divisibles par n.
Notation
Si a et b sont congruents modulo n, on écrira :
- a ≡ b (n) ou a ≡ b [n] ou encore a ≡ b (mod n)
ce qui se lit dans tous les cas « a est congru à b modulo n ».
Par exemple :
- 26 ≡ 12 (14)
Le caractère utilisé est ≡. Cependant, par commodité, il est parfois remplacé par = même si cela reste faux dans l'absolu .
Propriétés
Relation d'équivalence
La congruence modulo n a les propriétés suivantes :
- Pour tout entier a, a ≡ a (n)
- Symétrie :
- Pour tous entiers a et b, a ≡ b (n) ⇔ b ≡ a (n)
- Pour tous entiers a, b et c, si a ≡ b (n) et b ≡ c (n) alors a ≡ c (n)
C'est donc une relation d'équivalence.
Propriétés algébriques
Elle a de plus des propriétés algébriques remarquables :
Si
- a1 ≡ b1 (n) et a2 ≡ b2 (n)
alors
- a1 + a2 ≡ b1 + b2 (n)
et
- a1a2 ≡ b1b2 (n).
Enfin, avec un entier naturel q supérieur ou égal à 1, on obtient:
- a1q ≡ b1q (n).
DémonstrationPar hypothèse:
- a1 = x1 n + b1
- a2 = x2 n + b2
Pour l'addition:
- a1 + a2 = (x1 + x2) n + (b1 + b2 )
- Donc a1 + a2 ≡ b1 + b2 (n)
Multiplication:
- a1 a2 = x1 x2 n 2 + (x1 b2 + x2 b1) n + b1 b2
- a1 a2 = (x1 x2 n + x1 b2 + x2 b1) n + b1 b2
- Donc a1 a2 ≡ b1b2 (n)
Élévation à la puissance, par utilisation du binôme de Newton:- Donc a1q ≡ b1q (n).
On peut parler d'une certaine « compatibilité » avec les opérations d'addition et de multiplication des entiers, c'est-à-dire de « compatibilité » avec la structure d'anneau de (Z,+,*)). Ces quelques propriétés vont nous permettre de définir le domaine de l'arithmétique modulaire : les ensembles quotients Z/nZ.
Anneau résiduel Z/nZ
Article détaillé : Anneau Z/nZ.Construction
Les propriétés précédentes montrent que deux nombres congrus entre eux modulo n sont interchangeables dans une addition ou une multiplication, lors d'une congruence modulo n. L'idée vient alors de regrouper tous les nombres congrus entre eux modulo n dans une même classe que l'on appelle une classe d'équivalence et de ne travailler qu'avec un représentant particulier de cette classe. Comme tous les nombres de la même classe ont même reste dans la division par n, on privilégie les restes dans la division par n et on travaille sur un ensemble noté
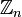 ou
ou 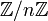 composé des n éléments
composé des n éléments 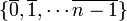 ou plus simplement {0, 1, 2, ... , n - 1} ensemble des restes modulo n, que l'on appelle anneau résiduel [1] modulo n ou encore anneau quotient [2]
ou plus simplement {0, 1, 2, ... , n - 1} ensemble des restes modulo n, que l'on appelle anneau résiduel [1] modulo n ou encore anneau quotient [2]Sur cet ensemble peuvent être définies une addition et une multiplication analogues à celles définies sur les entiers relatifs :
- Addition : à deux restes a et b, on associe le reste de a + b modulo n. On devrait théoriquement trouver une autre notation pour la somme, par exemple
 , mais, pour des raison de simplicité, on conserve souvent la même notation qui prend alors un sens différent.
, mais, pour des raison de simplicité, on conserve souvent la même notation qui prend alors un sens différent.
- ainsi dans l'anneau des congruences modulo 6, on écrira 3 + 2 = 5 mais 4 + 2 = 0 car la somme de 4 et 2 a pour reste 0 modulo 6
- Multiplication : à deux restes a et b, on associe le reste de a × b modulo n. Pour les mêmes raisons que précédemment, on utilise pour symbole du produit le même symbole que dans l'ensemble des entiers relatifs
- ainsi dans l'anneau des congruences modulo 6, on écrira 2 × 2 = 4, mais 2 × 5 = 4 (car le produit de 2 par 5 a pour reste 4 dans la division par 6) et même 2 × 3 = 0
On peut alors construire les tables d'opérations suivantes :
Table d'addition dans 
+ 0 1 2 3 4 5 0 0 1 2 3 4 5 1 1 2 3 4 5 0 2 2 3 4 5 0 1 3 3 4 5 0 1 2 4 4 5 0 1 2 3 5 5 0 1 2 3 4 Table de multiplication dans 
× 0 1 2 3 4 5 0 0 0 0 0 0 0 1 0 1 2 3 4 5 2 0 2 4 0 2 4 3 0 3 0 3 0 3 4 0 4 2 0 4 2 5 0 5 4 3 2 1
Ces opérations ont presque les mêmes propriétés que l'addition et la multiplication dans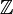 .
.- l'addition est commutative (les termes peuvent permuter), associative (lors de l'addition de 3 termes on peut faire indifféremment la somme des deux premiers et ajouter le dernier ou la somme des deux dernierset l'ajouter au premier), possède un élément neutre (ajouter 0 ne change rien) et chaque élément possède un opposé.
- Une nuance de taille en comparaison avec l'addition dans
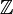 , c'est que, dans
, c'est que, dans 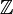 , l'opposé de a est - a car a + (- a) = 0. Or, dans l'anneau des congruences modulo n, l'opposé de a est n - a car a + (n - a) = 0 (la somme de a et de n - a a pour reste 0 dans la division par n). Cependant, - a et n - a sont interchangeables modulo n, le choix de n - a plutôt que - a tient au fait que l'on choisit comme représentant LE nombre compris entre 0 et n - 1.
, l'opposé de a est - a car a + (- a) = 0. Or, dans l'anneau des congruences modulo n, l'opposé de a est n - a car a + (n - a) = 0 (la somme de a et de n - a a pour reste 0 dans la division par n). Cependant, - a et n - a sont interchangeables modulo n, le choix de n - a plutôt que - a tient au fait que l'on choisit comme représentant LE nombre compris entre 0 et n - 1.
- Une nuance de taille en comparaison avec l'addition dans
- la multiplication est aussi commutative, associative, possède un élément neutre (multiplier par 1 ne change rien) et reste distributive pour l'addition.
Un ensemble muni de deux opérations ayant ces propriétés s'appelle un anneau.
Simplification et équations
La seule opération que l'on a l'habitude de faire dans
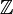 et qui n'est pas toujours juste dans l'anneau
et qui n'est pas toujours juste dans l'anneau 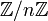 est la simplification.
est la simplification.- En effet si 2a = 4 dans
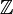 , on sait que a = 2. Mais, dans
, on sait que a = 2. Mais, dans  , si 2a = 4, on sait seulement que 2a a pour reste 4 dans la division par 6 donc que a a pour reste 2 dans la division par 3. a peut donc avoir pour reste dans la division par 6 soit 2 soit 5. Plus simplement : on a 2 × 2 = 2 × 5 sans pour autant avoir 2 = 5.
, si 2a = 4, on sait seulement que 2a a pour reste 4 dans la division par 6 donc que a a pour reste 2 dans la division par 3. a peut donc avoir pour reste dans la division par 6 soit 2 soit 5. Plus simplement : on a 2 × 2 = 2 × 5 sans pour autant avoir 2 = 5.
De même, la propriété constamment utilisée dans les ensembles de nombres classiques« pour qu'un produit de deux termes soit nul, il faut et il suffit que l'un des termes le soit » n'est pas toujours réalisée dans
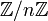
- dans
 , on a 2 × 3 = 0, sans que 2 ni 3 ne soient nuls
, on a 2 × 3 = 0, sans que 2 ni 3 ne soient nuls
On dit que l'anneau
 n'est pas intègre.
n'est pas intègre.La résolution d'équations peut donc devenir un peu problématique quand des multiplications sont en jeu :
- l'équation x + 2 = 1 dans
 se résout en ajoutant la même quantité (4) dans chaque membre x = 5 (car 2 + 4 = 0)
se résout en ajoutant la même quantité (4) dans chaque membre x = 5 (car 2 + 4 = 0) - l'équation 3x = 2 dans
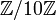 se résout en remarquant que 3 × 7 = 1 et que les équations 3x = 2 et x = 7 × 2 sont équivalentes (on passe de l'une à l'autre en multipliant chaque membre par 7 ou 3). La solution est alors égale à 4 (car 2 × 7 a pour reste 4 modulo 10)
se résout en remarquant que 3 × 7 = 1 et que les équations 3x = 2 et x = 7 × 2 sont équivalentes (on passe de l'une à l'autre en multipliant chaque membre par 7 ou 3). La solution est alors égale à 4 (car 2 × 7 a pour reste 4 modulo 10) - l'équation 2x = 3 dans
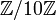 ne possède aucune solution et l'équation 2x = 6 en possède deux (3 et 8)
ne possède aucune solution et l'équation 2x = 6 en possède deux (3 et 8)
On montre que la résolution de l'équation ax = b d'inconnue x dans
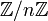 possède une unique solution si et seulement si a et n sont premiers entre-eux
possède une unique solution si et seulement si a et n sont premiers entre-euxLa recherche de solutions à l'équation
 qui peut avoir, selon les valeurs de n et de a, aucune, une, deux solutions, ou même davantage, donne lieu à l'étude des résidus quadratiques et à l'énoncé de la loi de réciprocité quadratique.
qui peut avoir, selon les valeurs de n et de a, aucune, une, deux solutions, ou même davantage, donne lieu à l'étude des résidus quadratiques et à l'énoncé de la loi de réciprocité quadratique.La construction de
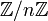 comme anneau quotienté par un idéal et les propriétés algébriques de l'anneau Z/nZ sont traités dans l'article Anneau Z/nZ
comme anneau quotienté par un idéal et les propriétés algébriques de l'anneau Z/nZ sont traités dans l'article Anneau Z/nZPuissances et petit théorème de Fermat
De la multiplication dans
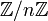 , il est naturel de s'intéresser aux puissances successives. Il n'y a que n - 1 restes possibles, donc n - 1 valeurs possibles pour ak, on obtient donc nécessairement plusieurs fois la même valeur. Donc, il existe k et m tels que ak et am ont le même reste modulo n. Comme la construction de ak est fondée sur une récurrence, dès que l'on tombe sur un reste déjà rencontré, on sait que la suite des puissances devient cyclique à partir de cette puissance et on peut arrêter l'exploration.
, il est naturel de s'intéresser aux puissances successives. Il n'y a que n - 1 restes possibles, donc n - 1 valeurs possibles pour ak, on obtient donc nécessairement plusieurs fois la même valeur. Donc, il existe k et m tels que ak et am ont le même reste modulo n. Comme la construction de ak est fondée sur une récurrence, dès que l'on tombe sur un reste déjà rencontré, on sait que la suite des puissances devient cyclique à partir de cette puissance et on peut arrêter l'exploration.Puissances successives dans 
1 2 3 4 5 6 k = 0 1 1 1 1 1 1 k = 1 1 2 3 4 5 6 k = 2 ... 4 2 2 4 1 k = 3 ... 1 6 1 6 ... k = 4 ... ... 4 ... 2 ... k = 5 ... ... 5 ... 3 ... k = 6 1 1 1 1 1 1 Puissances successives dans 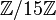
1 2 3 4 5 6 7 8 9 10 11 12 13 14 k = 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 k = 1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 k = 2 ... 4 9 1 10 6 4 4 6 10 1 9 4 1 k = 3 ... 8 12 ... 5 ... 13 2 9 ... ... 3 7 ... k = 4 ... 1 6 ... ... ... 1 1 ... ... ... 6 1 ... k = 5 ... ... 3 ... ... ... ... ... ... ... ... 12 ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... k = 8 1 1 ... 1 ... ... 1 1 ... ... 1 ... 1 1 Une observation sur les puissances dans
 et
et 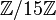 montre que, dans le premier cas, pour tout a premier avec 7 (c'est-à-dire non congru à 0 modulo 7), on a a6 congru à 1 modulo 7 et dans le second cas, les seules suites passant par 1 correspondent à des entiers premiers avec 15, il y a 8 entiers premiers avec 15 et on remarque que pour a premier avec 15, a8 est congru à 1 modulo 15.
montre que, dans le premier cas, pour tout a premier avec 7 (c'est-à-dire non congru à 0 modulo 7), on a a6 congru à 1 modulo 7 et dans le second cas, les seules suites passant par 1 correspondent à des entiers premiers avec 15, il y a 8 entiers premiers avec 15 et on remarque que pour a premier avec 15, a8 est congru à 1 modulo 15.Ces deux observations correspondent à deux théorèmes :
- le petit théorème de Fermat qui stipule que, pour tout entier n premier et tout entier a premier avec n,

- le théorème d'Euler, généralisation du théorème précédent, qui précise que, pour tout entier n supérieur ou égal à 2, et tout entier a premier avec n,
 , où
, où 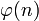 , indicatrice d'Euler, est le nombre d'entiers compris entre 1 et n - 1 et premiers avec n.
, indicatrice d'Euler, est le nombre d'entiers compris entre 1 et n - 1 et premiers avec n.
Notes et références
- ↑ résiduel veut dire " qui reste"
- ↑ le terme de quotient fait référence à la notion d'ensemble quotienté par une relation d'équivalence
Voir aussi
- Arithmétique élémentaire
- Divisibilité
- Critère de divisibilité
- Liste de critères de divisibilité
- Anneau Z/nZ
- Notion de module
- Portail des mathématiques
Catégorie : Arithmétique élémentaire
Wikimedia Foundation. 2010.