Compactification d'Alexandrov
- Compactification d'Alexandrov
-
Compactifié d'Alexandroff
Soit X un espace topologique séparé et localement compact, mais non compact. On peut, en ajoutant un point à X, obtenir un espace compact. Pour cela, on considère 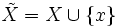 où
où 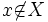 , et on définit une topologie de la manière suivante.
, et on définit une topologie de la manière suivante.
L'ensemble des ouverts de 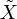 est constitué par :
est constitué par :
On vérifie alors que 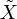 muni de cette topologie est un espace compact.
muni de cette topologie est un espace compact.
L'espace 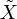 s'appelle alors le compactifié d'Alexandroff de l'espace localement compact X ; x s'appelle le point à l'infini de
s'appelle alors le compactifié d'Alexandroff de l'espace localement compact X ; x s'appelle le point à l'infini de 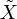 et se note également ∞.
et se note également ∞.
Exemples
Le compactifié d'Alexandroff de 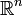 est homéomorphe à la sphère de dimension n.
est homéomorphe à la sphère de dimension n.
Par exemple le compactifié d'Alexandroff de 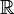 est un cercle, celui de
est un cercle, celui de 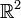 (ou
(ou 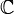 ) est une sphère, appelée communément sphère de Riemann.
) est une sphère, appelée communément sphère de Riemann.
Le point ajouté à l'espace peut être imaginé comme un point "à l'infini" : à l'infini la droite réelle se "referme" en un cercle.
Voir aussi
Compactification
 Portail des mathématiques
Portail des mathématiques
Catégories : Compacité | Théorème de mathématiques | Construction classique
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Compactification d'Alexandrov de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Pavel Alexandrov — For Russian footballer, see Pavel Aleksandrov (footballer). Pavel Sergeyevich Alexandrov Pavel Sergeyevich Alexandrov Born … Wikipedia
Compactifié d'Alexandrov — Compactifié d Alexandroff Soit X un espace topologique séparé et localement compact, mais non compact. On peut, en ajoutant un point à X, obtenir un espace compact. Pour cela, on considère où , et on définit une topologie de la manière suivante.… … Wikipédia en Français
Théorème d'Alexandrov — Compactifié d Alexandroff Soit X un espace topologique séparé et localement compact, mais non compact. On peut, en ajoutant un point à X, obtenir un espace compact. Pour cela, on considère où , et on définit une topologie de la manière suivante.… … Wikipédia en Français
Sphere de Riemann — Sphère de Riemann Pour les articles homonymes, voir Sphère (homonymie). En mathématiques, la sphère de Riemann est une manière de prolonger le plan des nombres complexes avec un point additionnel à l infini, de manière à ce que certaines… … Wikipédia en Français
Sphère de Gauss — Sphère de Riemann Pour les articles homonymes, voir Sphère (homonymie). En mathématiques, la sphère de Riemann est une manière de prolonger le plan des nombres complexes avec un point additionnel à l infini, de manière à ce que certaines… … Wikipédia en Français
Sphère de Riemann — Pour les articles homonymes, voir Sphère (homonymie). En mathématiques, la sphère de Riemann est une manière de prolonger le plan des nombres complexes avec un point additionnel à l infini, de manière à ce que certaines expressions mathématiques… … Wikipédia en Français
Sphère de riemann — Pour les articles homonymes, voir Sphère (homonymie). En mathématiques, la sphère de Riemann est une manière de prolonger le plan des nombres complexes avec un point additionnel à l infini, de manière à ce que certaines expressions mathématiques… … Wikipédia en Français
Compact space — Compactness redirects here. For the concept in first order logic, see compactness theorem. In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness… … Wikipedia
Alexandroff extension — In mathematical field of topology, the Alexandroff extension is a way to extend a noncompact topological space by adjoining a single point in such a way that the resulting space is compact. It is named for the Russian mathematician Pavel… … Wikipedia
List of Russian people — The Millennium of Russia monument in Veliky Novgorod, featuring the statues and reliefs of the most celebrated people in the first 1000 years of Russian history … Wikipedia
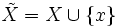 où
où 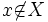 , et on définit une topologie de la manière suivante.
, et on définit une topologie de la manière suivante.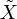 est constitué par :
est constitué par :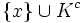 , où Kc est le complémentaire d'un compact K de X.
, où Kc est le complémentaire d'un compact K de X.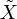 muni de cette topologie est un espace compact.
muni de cette topologie est un espace compact.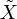 s'appelle alors le compactifié d'Alexandroff de l'espace localement compact X ; x s'appelle le point à l'infini de
s'appelle alors le compactifié d'Alexandroff de l'espace localement compact X ; x s'appelle le point à l'infini de 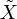 et se note également ∞.
et se note également ∞.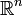 est homéomorphe à la sphère de dimension n.
est homéomorphe à la sphère de dimension n.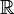 est un cercle, celui de
est un cercle, celui de 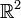 (ou
(ou 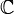 ) est une sphère, appelée communément sphère de Riemann.
) est une sphère, appelée communément sphère de Riemann.