- Compacite sequentielle
-
Compacité séquentielle
 Pour les articles homonymes, voir Compacité.
Pour les articles homonymes, voir Compacité.La compacité est une propriété topologique importante qui se définit en topologie générale, à partir de la notion de recouvrement ouvert. Toutefois dans le cadre des espaces métriques (comprenant notamment les espaces vectoriels normés), il est possible d'en donner une caractérisation en termes de suites. Il est fréquent de faire prendre à cette dernière le rôle d'une définition. La notion de compacité ainsi présentée est appelée compacité séquentielle.
Plusieurs propriétés des segments de la droite réelle se généralisent aux espaces compacts, ce qui confère à ces derniers un rôle privilégié dans divers domaines des mathématiques. Notamment ils sont utiles pour prouver l'existence d'extrema pour une fonction numérique.
Intuitivement, un ensemble compact est « petit » et « fermé », au sens où l'on ne peut « s'en échapper ». Si on forme une suite de points de cet ensemble, ses éléments ne peuvent pas beaucoup s'éloigner les uns des autres et se concentrent sur certaines valeurs. La propriété de compacité permet également de faire passer certaines propriétés du local au global. C'est-à-dire qu'une propriété vraie au voisinage de chaque point devient valable de façon uniforme sur tout le compact.
Cet article propose une approche progressive de la notion de compact. Ils sont présentés d'abord comme des parties fermées bornées d'un espace vectoriel réel de dimension finie, puis le cadre est élargi en se basant sur une définition séquentielle. La propriété de recouvrement, dite de Borel-Lebesgue, est enfin abordée. Les lecteurs qui souhaitent aborder directement les compacts dans le cadre de la topologie générale peuvent lire l'article compacité (mathématiques).
Sommaire
Première approche : fermés bornés en dimension finie
Lorsqu'on travaille sur la droite réelle, le plan usuel, ou plus généralement un espace vectoriel réel E de dimension finie, muni d'une norme, il est possible de prendre pour les compacts une définition provisoire, qui n'est équivalente à la définition générale que dans ce cadre particulier. On appellera donc partie compacte de E une partie K
- fermée, c'est-à-dire stable par passage à la limite (toute suite de points de K qui converge a sa limite dans K)
- et bornée : K peut être inclus dans une boule.
Une telle définition ne dépend pas de la norme choisie, puisqu'en dimension finie, les normes sont toutes équivalentes.
Les boules fermées de E constituent des exemples simples de compacts, mais rien n'oblige un compact à être « en un seul morceau » (voir connexité pour la formalisation de cette notion). Ainsi la réunion de deux boules fermées est encore un compact, ou également l'ensemble de Cantor.
Application à la recherche d'extrema
La compacité permet d'exhiber des extrema globaux pour les fonctions continues :
Théorème
Si f est une fonction continue définie sur un compact K, à valeurs réelles, alors f(K) est un compact de la droite réelle. Notamment f est bornée et atteint ses bornes.
La démonstration de ce théorème sera effectuée dans les deux paragraphes suivants. Quelques exemples de mise en œuvre permettent d'illustrer sa puissance.
Exemple : problème du point de Fermat.
- Un triangle ABC étant donné, il est demandé de prouver qu'il existe un point M tel que la somme des distances AM+BM+CM soit minimale. On remarque d'abord qu'il est inutile de chercher M trop loin des points A,B,C. La considération de l'application continue
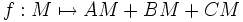 sur un disque fermé de rayon suffisamment grand permet d'appliquer le théorème : il existe un minimum global. Ce constat peut servir de point de départ à une construction explicite.
sur un disque fermé de rayon suffisamment grand permet d'appliquer le théorème : il existe un minimum global. Ce constat peut servir de point de départ à une construction explicite.
Exemple : distance d'un point à un fermé
- Soient F une partie fermée non vide de E et x un point de E. Il s'agit de prouver qu'il existe un point f de F plus proche de x que tous les autres. De nouveau, il est inutile de chercher f trop loin de x. On peut donc se limiter à l'intersection de F et d'une boule fermée, ce qui constitue un compact, et introduire la fonction distance à x qui est continue.
Remarque : le théorème sur l'image d'un compact rappelle le théorème d'analyse réelle « l'image d'un segment par une application continue est un segment ». Il n'en constitue cependant pas une véritable généralisation, puisqu'un compact n'est pas nécessairement un segment (précisément il manque l'évocation de la connexité). Enfin il ne faut pas le confondre avec l'énoncé « l'image réciproque d'un fermé par une application continue est un fermé ».
Propriété de Bolzano-Weierstrass
Soit K fermé borné. Toute suite d'éléments de K admet une valeur d'adhérence dans K, c'est-à-dire une sous-suite qui converge vers un point de K.
Cet énoncé porte parfois, assez improprement, le titre de théorème de Bolzano-Weierstrass. Le « vrai » théorème de Bolzano-Weierstrass sera évoqué plus bas.
Une stratégie de preuve est décrite dans l'article suite bornée ; elle consiste à travailler d'abord dans le cas réel où l'on dispose de propriétés de monotonie, puis à étendre au cas général.
- Autre démonstration, basée sur le critère de Cauchy.
- On traite d'abord un cas particulier : celui où K est un carré dans le plan usuel, d'arête de longueur unité.
- Soit donc une suite d'éléments (xn) de K. Le carré peut être découpé en quatre carrés d'arête moitié. Les termes de la suite se répartissent entre les quatre quartiers, et il y en a nécessairement une infinité dans un des quatre quartiers, qu'on note K1. On recommence la partition en découpant K1 en carrés d'arête un quart et en sélectionnant l'un d'eux, K2, qui contient une infinité de termes de la suite. On construit ainsi par récurrence une suite (Kp) de carrés inclus les uns dans les autres et d'arête de longueur 2 - p, qui contiennent chacun une infinité de termes de la suite.
- On prend alors un indice n0 tel que
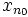 est dans K0, puis un indice strictement plus grand n1 tel que
est dans K0, puis un indice strictement plus grand n1 tel que 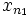 est dans K1 et ainsi de suite. On a ainsi construit une sous-suite
est dans K1 et ainsi de suite. On a ainsi construit une sous-suite 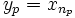 de la suite initiale, et qui vérifie pour tous p et q
de la suite initiale, et qui vérifie pour tous p et q 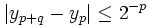
- C'est donc une suite convergente par le critère de Cauchy. Sa limite reste dans le carré puisque ce dernier est fermé.
- Généralisation : la démonstration peut être étendue à un cube en dimension trois, un hypercube en dimension quelconque, en adaptant simplement le nombre de morceaux du découpage. Elle s'étend ensuite à toute partie fermé borné, qui est incluse dans un tel hypercube.
Réciproquement, si une partie K de E vérifie la propriété de Bolzano-Weierstrass, elle est fermée et bornée.
- Démonstration
- La partie est fermée : si une suite de points de K converge vers l, elle admet une sous-suite qui converge dans K, mais qui converge aussi vers l, donc l est dans K
- La partie est bornée, sans quoi il est possible de construire une suite d'éléments dont les normes tendent vers l'infini ; toute sous-suite est alors divergente.
Application : démonstration du théorème sur l'image d'un compact
La caractérisation des compacts par la propriété de Bolzano-Weierstrass permet de prouver le théorème sur l'image directe d'un compact par une application continue.
- Démonstration
- Il suffit de montrer que f(K) vérifie la propriété de Bolzano-Weierstrass. Si (yn) est une suite de points de f(K), avec yn=f(xn), alors la suite (xn) admet une sous-suite convergeant vers X élément de K. Par continuité, la suite des images converge vers f(X) qui appartient à f(K).
Contre-exemple en dimension infinie
Considérons l'espace vectoriel
![E=\mathbb{R}[X]](/pictures/frwiki/97/afc3aacd66809df64a8b61988b688a22.png) des polynômes à coefficients réels. On prend pour norme du polynôme P le maximum des valeurs absolues de ses coefficients. Soit B la boule unité fermée, elle est clairement fermée et bornée. Cependant la suite de polynômes Xn, qui sont tous éléments de B, n'admet aucune sous-suite convergente (en effet deux termes de cette suite sont à distance 1). On pourrait également construire une application f, continue de E dans
des polynômes à coefficients réels. On prend pour norme du polynôme P le maximum des valeurs absolues de ses coefficients. Soit B la boule unité fermée, elle est clairement fermée et bornée. Cependant la suite de polynômes Xn, qui sont tous éléments de B, n'admet aucune sous-suite convergente (en effet deux termes de cette suite sont à distance 1). On pourrait également construire une application f, continue de E dans  , telle que f(Xn)=n, donc non bornée.
, telle que f(Xn)=n, donc non bornée.Dans un espace vectoriel de dimension infinie, les espace fermés bornés ne jouissent plus tous des propriétés intéressantes d'analyse qui avaient été observés en dimension finie.
Les compacts dans le cadre des espaces métriques
De très nombreux problèmes de topologie et d'analyse fonctionnelle se posent dans le cadre des espaces vectoriels normés de dimension quelconque, ou plus généralement des espaces métriques. L'outil principal est alors la notion de suite convergente.
Définition séquentielle
Dans ce cadre, il est possible d'adopter une définition séquentielle des compacts, en les définissant comme les parties vérifiant la propriété de Bolzano-Weierstrass. Ainsi K sera un compact si et seulement si de toute suite d'éléments de K on peut extraire une sous-suite qui converge dans K.
Dans le cas particulier d'un espace vectoriel normé de dimension finie, on a vu que les compacts sont les parties fermées bornées. En général, les compacts sont encore des parties fermées et bornées, mais la réciproque est fausse.
En reprenant la démonstration faite précédemment, l'image d'un compact par une application continue est un compact.
Exemples d'espaces compacts
Dans un espace vectoriel normé, une boule fermée est compacte si et seulement si l'espace est de dimension finie : c'est le théorème de Riesz.
Recouvrements ouverts
Article détaillé : Propriété de Borel-Lebesgue.Un espace topologique non vide K est dit compact s'il est séparé, et si de tout recouvrement ouvert de K on peut extraire un sous-recouvrement fini. voir Théorème de Borel-Lebesgue
Parties compactes
- Une partie K d'un espace topologique X est dite compacte si le sous-espace topologique K, muni de la topologie induite, est compact.
- Une partie K d'un espace topologique X est dite relativement compacte si son adhérence
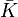 est une partie compacte de X.
est une partie compacte de X.
Cas des espaces métriques
- Un espace métrique K est dit précompact s’il en existe des recouvrements par des boules ouvertes arbitrairement petites, soit :

Propriété : Un espace métrique est compact si et seulement s’il est précompact et complet
- ATTENTION : Il faut se garder, dans le cas général, de dire que si un espace est compact alors il est complet et précompact ; en effet ces deux dernières notions sont métriques et n'ont donc aucun sens dans le cadre de la topologie générale. La compacité par contre est une notion « purement topologique ».
Propriété : Un espace métrique compact (ou une partie compacte d'un espace métrique) est borné(e). Il suffit en effet de considérer comme recouvrement les boules ouvertes de même centre et de rayon n ou n est entier. C'est un recouvrement, un recouvrement fini est inclus dans une boule et la propriété est démontrée.
Diverses propriétés
Opérations ensemblistes, théorème de Tychonoff
Propriété : Soit E un espace topologique, K1 et K2 deux parties compactes de E. Alors
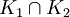 et
et 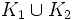 sont compactes.
sont compactes.Propriété : Soit K1 et K2 deux espaces compacts ; le produit
 , muni de la topologie produit, est encore compact.
, muni de la topologie produit, est encore compact.Théorème (de Tychonoff) : Un produit quelconque de compacts est compact, i.e. : si
 est une famille quelconque d'espaces compacts, alors le produit
est une famille quelconque d'espaces compacts, alors le produit 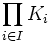 est encore un espace compact. (Ce théorème nécessite l'axiome du choix pour sa démonstration.)
est encore un espace compact. (Ce théorème nécessite l'axiome du choix pour sa démonstration.)Compacité et continuité, théorème de Heine
Propriété : Soit E, F des espaces topologiques, F étant séparé, K une partie compacte E, et f une application continue de E vers F. Alors f(K) est compact.
Moralité : l'image continue d'un compact (dans un séparé) est compacte.
Corollaire : Soit K un espace compact, et f une application continue de K vers
 . Alors f est bornée et atteint ses bornes.
. Alors f est bornée et atteint ses bornes.Propriété : Soit K un espace compact, F un espace séparé, et f une bijection continue de K vers F. Alors f est un homéomorphisme.
Théorème (de Heine) : Soit K un espace compact, F un espace métrique, f une application continue de K vers F. Alors f est uniformément continue.
Espaces métriques compacts
Dans le cas où l'on dispose d'une distance sur l'espace, on peut tirer de la compacité de nombreuses informations. On a déjà vu les interactions avec la complétude et la précompacité. On peut également caractériser la compacité à l'aide du théorème fondamental suivant.
Le théorème de Bolzano-Weierstrass
On dira qu'un espace métrique E possède la propriété P si pour toute suite de points de E, on peut extraire une sous-suite convergeant vers un point de E.
Cette propriété se dit également : toute suite d'éléments de E a une valeur d'adhérence dans E.
NB: Le fait que la limite soit dans l'espace est fondamental ; par exemple toute suite de points de [0,1[ admet une sous-suite convergente dans
 mais la limite peut être 1.
mais la limite peut être 1.Théorème (de Bolzano-Weierstrass) : Un espace métrique est compact si et seulement s’il vérifie la propriété P.
De là la forme habituelle du « théorème de Bolzano-Weierstrass » dans
 : toute suite réelle bornée admet une sous-suite convergente.
: toute suite réelle bornée admet une sous-suite convergente.Séparabilité, cardinalité
Théorème : Un espace métrique compact est séparable.
Corollaire : Un espace métrique compact a au plus la puissance du continu, i.e. il est de cardinal inférieur ou égal à celui de
 .
.Voir aussi
- Espace topologique
- Espace métrique
- Espace complet
- Espace localement compact
- Analyse réelle, Analyse complexe
- Suite (mathématiques)
- Le glossaire topologique pour plus de précisions terminologiques, notamment pour les différents niveaux de « séparation » ; on entend ici « de Hausdorff » pour séparé.
- Portail des mathématiques
Catégories : Compacité | Espace métrique
Wikimedia Foundation. 2010.
