- Combinaison (Mathématiques)
-
Combinaison (mathématiques)
 Pour les articles homonymes, voir combinaison.
Pour les articles homonymes, voir combinaison.En mathématiques, lorsque nous choisissons k objets parmi n objets discernables (numérotés de 1 à n) et que l’ordre dans lequel les objets sont placés (ou énumérés) n’a pas d’importance, nous pouvons les représenter par un ensemble à k éléments. Les combinaisons servent donc, entre autres, en combinatoire. Par exemple, quand nous tirons simultanément plusieurs cartes dans un jeu de cartes, nous obtenons une main et la place des cartes dans la main n’importe pas ; ou au jeu du loto, le tirage final ne dépend pas de l’ordre d’apparition des boules obtenues.
Sommaire
Définition mathématique
Définition
Soient E un ensemble fini de cardinal n et k un entier naturel. Les combinaisons de cet ensemble sont ses sous-ensembles (ou ses parties). Une k-combinaison de E (ou k-combinaison sans répétition de E, ou encore combinaison sans répétition de n éléments pris k à k) est une partie à k éléments de E.
Nous notons
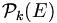 l’ensemble des k-combinaisons de E.
l’ensemble des k-combinaisons de E.L’ensemble
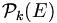 des combinaisons à k éléments de E, est fini et son cardinal se note traditionnellement en France
des combinaisons à k éléments de E, est fini et son cardinal se note traditionnellement en France 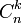 , mais de plus en plus
, mais de plus en plus 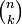 , comme dans les autres pays, et
, comme dans les autres pays, et 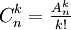 , où
, où 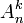 est le nombre de k-arrangements de E.
est le nombre de k-arrangements de E.Si k ≤ n alors
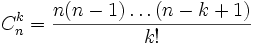 qui peut aussi s'écrire :
qui peut aussi s'écrire : 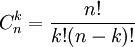 .
.Démonstration
- Si k = 0 alors il n’y a qu’une seule partie à 0 élément, l’ensemble vide, donc
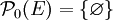 . Mais
. Mais 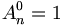 et 0! = 1 d’où l’égalité.
et 0! = 1 d’où l’égalité. - Si k > n alors il n’existe pas de partie à k éléments dans un ensemble à n éléments, donc
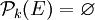 et comme
et comme 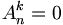 , la formule est vérifiée.
, la formule est vérifiée. - Si 1 ≤ k ≤ n alors nous définissons sur l’ensemble des arrangements sans répétitions de E (ou des k-listes distinctes de E) une relation d’équivalence :
Deux arrangements sont équivalents, s’il existe une permutation à k éléments qui envoie l’un sur l’autre. Deux arrangements sont alors équivalents si et seulement s’ils correspondent à la même partie à k éléments de E. Une classe d’équivalence est alors une combinaison et il y a autant de classes que de combinaisons. Mais chaque classe contient k! arrangements qui sont en relation ; d’après la réciproque du lemme des bergers il y a donc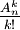 classes ou combinaisons.
classes ou combinaisons.
Calcul du nombre de combinaisons
Un algorithme efficace[1] pour calculer le nombre de combinaisons de k éléments parmi n, utilise les identités suivantes (0 ≤ k ≤ n) :
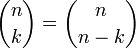 ,
, 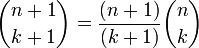 et
et 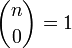
La première permet de réduire le nombre d'opérations à effectuer en se ramenant à k ≤ n/2. Les deux suivantes permettent de montrer que :
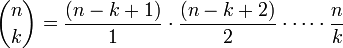
À chaque étape de calcul on effectue d'abord la multiplication puis la division pour obtenir un nombre entier (c'est un coefficient binomial), c'est-à-dire que l'on peut employer la division entière. Les calculs intermédiaires restent d'un ordre de grandeur voisin du résultat final (ce ne serait pas le cas si par exemple on utilisait la première formule et la fonction factorielle).
Le calcul peut s'effectuer par une simple boucle itérative (boucle for).
Exemple en pratique d'un calcul de combinaisons :
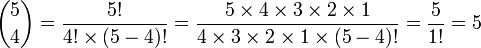
On voit que la division des factorielles de 5 et de 4 ont été directement simplifiées :
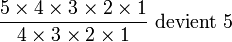
Énumération des combinaisons
Soient A un ensemble à n éléments, b un objet qui n'est pas dans A, et k un entier naturel. Alors on montre facilement l'identité :
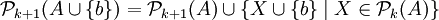 (
(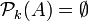 si k > n)
si k > n)(cette identité est connue pour avoir pour conséquence directe la formule de récurrence permettant de construire le triangle de Pascal :
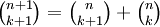 ) Cette identité peut être exploitée pour un algorihme énumérant les combinaisons, par exemple des n premiers entiers.
) Cette identité peut être exploitée pour un algorihme énumérant les combinaisons, par exemple des n premiers entiers.Notes
- ↑ C'est par exemple celui utilisé par la bibliothèque de programmes de calcul arithmétique en précision arbitraire GMP, voir (en) Binomial coefficients algorithm.
Voir aussi
Liens internes
- Coefficient binomial
- Combinatoire
- Combinaison avec répétition
- Arrangement
- Arrangement avec répétition
- Permutation
- Permutation avec répétition
- Portail des mathématiques
Catégorie : Analyse combinatoire - Si k = 0 alors il n’y a qu’une seule partie à 0 élément, l’ensemble vide, donc
Wikimedia Foundation. 2010.
