- Coloration De Graphe
-
Coloration de graphe
En mathématiques, la coloration de graphe renvoie à un champ d'études appartenant à la théorie des graphes. Il s'agit de déterminer combien de couleurs différentes suffisent pour colorer entièrement un graphe de telle façon qu'aucun nœud du graphe n'ait la même couleur que les nœuds voisins.
Historiquement, ce problème s'est posé lorsqu'il s'agissait de colorer une carte des pays de façon qu'aucun pays n'ait la même couleur que ses voisins.
Sommaire
Introduction
Le problème de la coloration de graphe est à l'origine même de la théorie des graphes, et au moins deux théorèmes phares de cette théorie et de l'optimisation combinatoire concernent la coloration :
- le célèbre théorème des quatre couleurs, et
- le théorème des graphes parfaits.
Il a fallu plus d'un siècle pour démontrer le théorème des quatre couleurs, et plus de 40 ans pour démontrer le théorème des graphes parfaits. Au XXIe siècle, la coloration est un domaine de recherche vivace, dans la mesure où il contient encore de nombreuses conjectures qui résistent depuis une cinquantaine d'années (voir plus bas).
L'origine de la coloration remonte à la question suivante : peut-on colorer chacune des faces d'un polyèdre (de notre espace usuel en 3D) sans que deux faces adjacentes aient la même couleur en n'utilisant que quatre couleurs au maximum ? Ce problème dépend uniquement de la structure combinatoire de graphe planaire que l'on peut associer naturellement à tout polyèdre (les faces correspondent aux sommets et l'adjacence entre faces à l'adjacence entre sommets). L'extension du problème aux graphes quelconques (pas nécessairement planaires) a trouvé sa motivation théorique principale avec la conjecture de Berge (maintenant c'est le théorème des graphes parfaits). L'extension aux graphes quelconques est aussi motivée par diverses applications concrètes, notamment dans l'allocation de fréquences (voir plus bas).
Donnons maintenant une définition du problème.
Définition (nombre chromatique)
La notion de coloration n'est définie que pour les graphes sans boucle, et la multiplicité des arêtes ne joue aucun rôle. Donc, soit G un graphe simple (sans boucle ni arête multiple), un stable de G est un sous-ensemble de sommets deux-à-deux non-adjacent, et
- une coloration de G est une partition de son ensemble de sommets en stables.
La définition originale de la coloration est la suivante:
- une coloration de G est une fonction associant à tout sommet de G une couleur, généralement un élément de l'ensemble d'indices des couleurs {1,2,...,n}, telle que deux sommets adjacents n'ont pas la même couleur (où n est le nombre de sommets du graphe).
On lui préfère généralement la définition que nous avons donnée en premier, car, pour la plupart des questions liées au concept de coloration, on ne souhaite pas différencier les colorations qui ne sont distinctes qu'à permutation des indices de couleurs près (ce qui est le cas pour le problème central lié à la coloration, celui de déterminer le nombre minimum de couleur dans une coloration de G, c'est-à-dire son nombre chromatique). Par-exemple, si G est constitué de deux sommets u et v et d'une arête les reliant, alors les deux fonctions f et g avec f(u)=1, f(v)=2, et g(u)=2, g(v)=1 sont des colorations différentes pour la deuxième définition mais équivalentes pour la première.
Dans ses différents ouvrages (en français ou en anglais), Berge a utilisé les deux notations γ(G) et χ(G) pour désigner le nombre chromatique de G[1]. De nos jours, la plupart des ouvrages adoptent le symbole χ(G) (tandis que γ(G) concerne plutôt un invariant lié au concept de cycle).
Enfin, dans certains contextes, on parle aussi de coloration pour désigner une fonction associant une couleur aux sommets d'un graphe mais satisfaisant d'autres propriétés (e.g. dans le contexte de l'optimisation de la génération de code sur une machine comportant un grand nombre de registres).
Conjectures, questions ouvertes
Conjecture d'Hadwiger
La plus célèbre des conjectures est sans doute celle d'Hadwiger en 1943. Le nombre d'Hadwiger d'un graphe G est égal au plus grand entier k tel que G ait un mineur isomorphe au graphe complet à k sommets.
- Pour tout graphe sans boucle G, le nombre chromatique de G est inférieur ou égal au nombre d'Hadwiger de G.
La conjecture d'Hadwiger est déjà démontrée pour les graphes dont le nombre d'Hadwiger est au plus 6, la preuve est basée sur le théorème des quatre couleurs[2].
Problème de Hadwiger–Nelson
- Déterminer le nombre chromatique du graphe dont les sommets sont les points du plan (euclidien) et tel que deux sommets sont adjacents si la distance qui les sépare vaut 1.
Une autre formulation est :
- Quel est le nombre minimal de couleurs qu'il faut pour pouvoir colorier tout graphe distance-unité ?
D'après Tommy Jensen et Bjarne Toft[3], le problème fut posé pour la première fois par E. Nelson en 1950 et publié pour la première fois par Gardner en 1960[4]. Hugo Hadwiger avait cependant publié un résultat en rapport avec le probème dès 1945[5].
Actuellement, tout ce qu'on l'on peut dire c'est que ce nombre est compris entre 4 et 7. La borne inférieure s'obtient en remarquant que les sommets d'un triangle équilatéral de côté 1 sont nécessairement de trois couleurs différentes. Ainsi, si l'on pouvait colorier le plan avec uniquement 3 couleurs, on peut prouver en collant deux triangles équilatéraux de côté 1 par un coté commun que deux points distants de racine de 3 sont forcément de la même couleur ; on parvient alors à une contradiction en considérant un triangle isocèle dont deux cotés sont de longueur racine de 3 et un coté de longueur 1. La borne supérieure s'obtient à partir d'un pavage hexagonal du plan. Certains résultats concernant cette conjecture dépendent de l'axiome du choix.
Conjecture de Grünbaum
- Pour tout m>1 et n>2 il existe un graphe n-régulier de nombre chromatique m et de maille au moins n[6].
Le résultat est trivial pour n=2 et m=2,3 mais pour m>3 seuls peu de graphes illustrant la conjecture sont connus. Le graphe de Chvátal est l'un d'eux.
Un exemple d'application : l'allocation de fréquences
Bien sûr, les applications concernent les graphes finis. Certains réseaux de télécommunication sont composés d'émetteurs émettant chacun sur une fréquence particulière. Lorsque deux émetteurs sont trop proches on ne peut leur allouer la même fréquence à cause des interférences (sauf si éventuellement une montagne les sépare).
On associe un graphe au réseau—chaque sommet est un émetteur et chaque arête spécifie que l'on ne veut pas allouer la même fréquence aux deux émetteurs correspondant à ses deux extrémités—et ainsi déterminer une allocation réalisable avec un minimum de fréquences (dont la licence d'exploitation peut entrainer un coût important). Ce problème est un cas particulier du problème de la coloration de graphe.
Précisons que les contraintes technologiques dépendant du relief géographique, on ne peut pas faire l'hypothèse qu'un graphe obtenu à partir des réseaux de télécommunications soit un graphe de disques.
Pour certains problèmes d'allocation de fréquences, on peut être amené à allouer plusieurs fréquences à un même émetteur; à imposer un écart minimum entre les fréquences allouées à deux émetteurs proches (et non plus seulement qu'elles soient distinctes); à imposer d'allouer à un émetteur une fréquence choisie parmi seulement un sous-ensemble des fréquences disponibles… La coloration apparaît alors comme un cas particulier de ces variantes.
Aspects algorithmiques généraux
Déterminer le nombre chromatique d'un graphe est un problème NP-complet dans le cas général. En fait, on peut en dire plus si l'on considère le problème de décision suivant : soit G un graphe et k un entier, peut-on colorer G avec moins de k couleurs ?
Si k=2 il s'agit de décider si G est biparti ou non. Ceci est facile car ces graphes sont caractérisés par la non-présence d'une structure interdite : celle de cycle impair. Par contre pour tout k fixé supérieur à 3 le problème devient NP-complet.
Ainsi, à moins que P=NP, il n'existe pas d'algorithme polynomial déterminant le nombre chromatique d'un graphe arbitraire. Pour certaines classes de graphes par contre de tels algorithmes existent. C'est notamment le cas pour les graphes triangulés (ou chordaux) dans lesquels le problème se résout en temps linéaire. Un résultat nettement plus difficile (de László Lovász et al.) établit (en développant toute une théorie) que l'on peut déterminer en temps polynomial le nombre chromatique de tout graphe parfait (pour une définition voir Théorème des graphes parfaits).
Parmi les algorithmes exacts (donc de complexité exponentielle dans le cas général) citons l'algorithme de Zykov (par la méthode de Branch and Bound). L'importance du problème a donné lieu à l'élaboration de nombreuses heuristiques spécifiques au problème, spécialement des algorithmes séquentiels de coloration sommet par sommet (dsatur, cosine, maya, etc.). Elle a aussi suscité de nombreuses expérimentations des méthodes approchées générales : méta-heuristique (recuit simulé, recherche tabou), ou encore algorithme génétique…
Donnons quelques heuristiques spécifiques au problème de la coloration.
Heuristiques
Algorithme de Welsh et Powell
Voici un exemple qui, en plus, fournit une preuve constructive du théorème de Vizing, qui établit la formule :
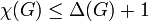 , où Δ(G) représente le degré maximum d'un sommet de G (le degré d'un sommet étant le nombre des arêtes qui lui sont incidentes). Pour s'en convaincre, appliquons l'algorithme suivant (Welsh et Powell) :
, où Δ(G) représente le degré maximum d'un sommet de G (le degré d'un sommet étant le nombre des arêtes qui lui sont incidentes). Pour s'en convaincre, appliquons l'algorithme suivant (Welsh et Powell) :- Repérer le degré de chaque sommet.
- Ranger les sommets par ordre de degrés décroissants (dans certains cas plusieurs possibilités).
- Attribuer au premier sommet (A) de la liste une couleur.
- Suivre la liste en attribuant la même couleur au premier sommet (B) qui ne soit pas adjacent à (A).
- Suivre (si possible) la liste jusqu'au prochain sommet (C) qui ne soit adjacent ni à A ni à B.
- Continuer jusqu'à ce que la liste soit finie.
- Prendre une deuxième couleur pour le premier sommet (D) non encore colorié de la liste.
- Répéter les opérations 4 à 6.
- Continuer jusqu'à avoir coloré tous les sommets.
Remarquons que cette méthode peut aboutir à la pire des colorations possibles, par-exemple si le graphe G a la structure de couronne à n sommets (voir http://en.wikipedia.org/wiki/Crown_graph), son nombre chromatique est 2 tandis que Welsh-Powell donne dans certains cas (selon l'ordre dans lequel sont rangés les sommets) une coloration utilisant n/2 couleurs ! L'heuristique DSATUR permet d'éviter ce problème et donne une coloration moins mauvaise dans le pire cas.
DSATUR
On considère un graphe G=(V,E) simple connexe et non-orienté. Pour chaque sommet v de V, on calcule le degré de saturation DSAT(v) de la manière suivante:
Si aucun voisin de v n'est coloré alors DSAT(v)=degré(v) sinon DSAT(v)= le nombre de couleurs différentes utilisées dans le premier voisinage de vL'algorithme DSATUR est un algorithme de coloration séquentiel, au sens où il colorie un seul sommet à la fois et tel que:
au départ le graphe n'est pas coloré on colorie un sommet non déjà coloré on stoppe DSATUR quand tous les sommets de G sont colorés.
Dans un premier temps on voit bien d'une part que la preuve de terminaison est triviale et d'autre part que l'algorithme est séquentiel. Dans le détail l'algorithme est le suivant :
1. Ordonner les sommets par ordre décroissant de degré. 2. Colorer un sommet de degré maximum avec la couleur 1. 3. Choisir un sommet non coloré avec DSAT maximum. Si conflit choisir celui avec degré maximum. 4. Colorer ce sommet par la plus petite couleur possible 5. Si tous les sommets sont colorés alors stop. Sinon aller en 3.Implémentations des heuristiques présentées
A titre illustratif, voici une implémentation (partielle) de Welsh-Powell en Fortran 95:
!----------------------! ! ! ! Algo de Welsh Powell ! !______________________! function WP(M,nu_heuristique) result(RES) logical, dimension(:,:), intent(in) :: M integer, intent(in) :: nu_heuristique TYPE(VOISIN), dimension(:), pointer :: TMP,TMP1,TMP2 integer, dimension(:),pointer :: RES integer :: h,i,j,color,last_color i=0 ! nbre de sommets colorés j=1 ! indice du prochain sommet à traiter color=1 ! couleur du prochain sommet à colorer allocate(RES(0:size(M,1))) ! DETERMINATION DE L'HEURISTIQUE A UTILISER : if (nu_heuristique==0) then ! version brute call CONV_VOISINS(M,TMP) else ! version plus fine : call CONV_VOISINS_TRIE(M,TMP) end if RES=0 ! tant que tous les sommets ne sont pas marqué do while(j<=size(M,1)) ! si le sommet courant n'est pas marqué if (RES(TMP(j)%NUM)==0) then RES(TMP(j)%NUM)=color ! on colorie le sommet i=i+1 last_color=color ! on cherche les non voisins de j dans l'ensemble de la matrice call POINTS_NON_VOISINS(TMP,TMP(j)%NUM,TMP1) ! tant qu'il reste des non voisins h=1 do while(h<=size(TMP1,1)) if (RES(TMP1(h)%NUM)==0) then RES(TMP1(h)%NUM)=color i=i+1 ! et on déduit le sous ensemble n'étant ni voisin de j et des sommets déjà marqué call POINTS_NON_VOISINS(TMP1,TMP1(h)%NUM,TMP2) if (size(TMP2)==0) exit call COPIE(TMP2,TMP1) h=0 end if h=h+1 end do j=j+1 ! on passe au sommet suivant color=color+1 ! ainsi qu'à la couleur suivante else j=j+1 ! sinon on passe au sommet suivant end if end do RES(0)=last_color end function WP
Voir aussi
Références
- ↑ Claude Berge, Hypergraphes. Combinatoires des ensembles finis, Bordas, 1987
- ↑ (en) Robertson, Neil; Seymour, Paul; Thomas, Robin (1993). "Hadwiger's conjecture for K6-free graphs". Combinatorica 14, 279-361
- ↑ (en) Tommy R. Jensen et Bjarne Toft, Graph Coloring Problems, Wiley-Interscience Series in Discrete Mathematics and Optimization, 1995, p. 150–152
- ↑ (en) Martin Gardner, Mathematical Games, vol. 203/4, 1960, p. 180
- ↑ Hugo Hadwiger, « Überdeckung des euklidischen Raumes durch kongruente Mengen », dans Portugal. Math., vol. 4, 1945, p. 238–242
- ↑ (en) Grünbaum, B. "A Problem in Graph Coloring." Amer. Math. Monthly 77, 1088-1092, 1970
- Portail des mathématiques
Catégories : Problème NP-complet | Théorie des graphes | Théorème de mathématiques
Wikimedia Foundation. 2010.

