Calcul Des Variations

Calcul des variations

En analyse fonctionnelle, le calcul des variations (ou calcul variationnel) est un ensemble de méthodes permettant de déterminer les points critiques ou les extrémales de fonctionnelles à l'aide de l'équation d'Euler-Lagrange.

L'application des théories de Galois, d'Abel et de la transformée de Laplace permit d'en faire toute une branche fructueuse des mathématiques. Elle trouve de nombreuses applications en physique mathématique, comme les principes variationnels ou la recherche de courbes ou surfaces minimales comme celles associées aux théorèmes isopérimétriques, de courbes brachistochrones et de géodésiques.

Variations première et seconde

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Équation de Jacobi

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Points conjugués et condition de Legendre

Cette section est vide, pas assez détaillée ou incomplète. Votre aide est la bienvenue !

Condition de Weierstrass

Karl Weierstrass (1815-1897)

Condition de Weierstrass

Revenons-en à l'expression de l'intégrale

$W = \int_{x_0}^{x_1} f(x,y,y')\;\mathrm dx$

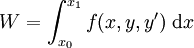
et considérons un champ F d'extrémales se composant d'une famille de ces courbes à un paramètre α. Chacune d'elles satisfait naturellement à l'équation d'Euler-Lagrange :

$\frac{\mathrm d}{\mathrm dx}\frac{\partial f}{\partial y'} - \frac{\partial f}{\partial y} = 0$.

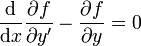En adoptant la représentation paramétrique : x₀, x₁ et α, fonctions de t, x₀ et x₁ décrivent des courbes C et D lorsque t varie, et la variation de W d'une extrémale à l'autre est^[1]

$\delta W = \left[ \left( f + \frac{\partial f}{\partial y'} (Y' - y') \right) \delta x \right]_{0 \to 1}$,

où y' est le coefficient angulaire de la tangente à l'extrémale et Y' celui de la tangente à la courbe C ou D.

Notes

1. ↑ En tenant compte de la formule $\textstyle\delta W = [L_1\,\delta t_1]_{Q'_1P_1} - [L_0\,\delta t_0]_{Q'_0P_0} + \int_{(Q'_0, t_0)}^{(Q'_1, t_1)} L\;\mathrm dt - \int_{(Q_0, t_0)}^{(Q_1, t_1)} L\;\mathrm dt$ établie plus haut.

Voir aussi

Bibliographie

• H. Goldstein (1980). Classical Mechanics (Second Edition), Addison-Wesley Publishing Company, Reading, Massachusetts. ISBN 0-201-02969-3.

Liens internes

• Principe variationnel
• Principe variationnel en physique quantique
• Équation d'Euler-Lagrange
• Courbe brachistochrone
• Lemme fondamental du calcul des variations

Ce document provient de « Calcul des variations ».