Théorème japonais pour les quadrilatères inscriptibles

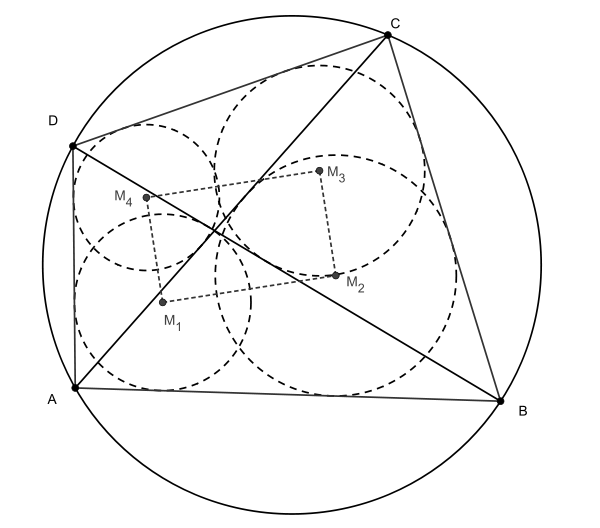
En géometrie, le théorème japonais pour les quadrilatères dit que les centres des cercles inscrits des triangles d'un quadrilatère inscriptible sont les sommets d'un rectangle.

En traçant les diagonales du quadrilatère, on obtient quatre triangles (chaque diagonale crée deux triangles). Les centres des cercles inscrits dans ces triangles forment un rectangle.

Énoncé

Soit ABCD un quadrilatère inscriptible quelconque et soient M₁,M₂,M₃,M₄ les centres des cercles inscrits dans les triangles ABD,ABC,BCD,ACD. Alors le quadrilatère M₁,M₂,M₃,M₄est un rectangle.

Principe de la démonstration

La démonstration s'appuie sur deux propriétés sur les angles

• Dans un triangle ABC dont le centre du cercle inscrit est O, l'angle BOC est égal à la moitié de l'angle BAC augmenté d'un angle droit,
• La propriété des angles inscrits pour des points cocycliques

On démontre alors que les points ABM₁M₂ sont cocycliques, ainsi que queADM₁M₄, etc. On prouve alors que l'angle M₂M₁M₄ est droit en l'écrivant à l'aide des anglesM₂M₁A et M₄M₁A

Prolongement

Ce théorème est une étape dans la démonstration d'un théorème plus général , concernant les rayons des cercles inscrits, le théorème japonais qui stipule dans le cadre de ce quadrilatère, que la somme des rayons des cercles inscrits de centre M₁et M₃ est égale à la somme des rayons des cercles inscrits de centres M₂ et M₄. Pour prouver le cas des quadrilatères inscriptibles, il faut construire le parallélogramme dont les côtés passent par les sommets du rectangle tout en étant parallèles aux diagonales du quadrilatère. On démontre alors que le parallélogramme obtenu est un losange, en se servant des angles alternes-internes et de la cyclicité des points ABM₁M₂, etc. Les distances entre les côtés opposés de ce losange sont donc égales, ce qui revient à dire que la somme des rayons des cercles inscrits tangents à chaque diagonale sont égaux.

Le cas du quadrilatère prouve immédiatement le cas général par la triangulation d'un polygone.

Voir aussi

• Théorème de Carnot
• Sangaku
• Wasan

Références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Japanese theorem for cyclic quadrilaterals » (voir la liste des auteurs)

Liens externes

• Japanese theorem, interactive proof with animation
• Jean-Louis Ayme Le rectangle de Ryokan Maruyama pour l'aspect historique et une réciproque.