Preuve sans mots

 Ne doit pas être confondu avec Avec les mains.

En mathématiques, une preuve sans mots (ou une démonstration visuelle) est une démonstration d'une identité (ou d'une affirmation mathématique plus générale) à l'aide d'un diagramme la rendant évidente, sans qu'un texte plus explicite le commentant soit nécessaire. Quand le diagramme n'en illustre qu'un cas particulier, il faut que sa généralisation ne demande au lecteur qu'un effort minimal^[1]. Malgré les risques qu'elles présentent, ces démonstrations sont souvent considérées comme plus élégantes que des preuves mathématiquement plus rigoureuses^[2].

Exemples

Compte tenu de la définition de ces preuves, les commentaires qui suivent devraient être presque complètement redondants, pour quiconque connait le résultat à démontrer ; on trouvera cependant des analyses plus détaillées des premières dans l'article algèbre géométrique, cet article donnant également un historique de certaines de ces preuves, et offrant quelques considérations sur la valeur qu'il faut leur accorder.

Une preuve sans mots de ce que la somme des nombres impairs est un carré parfait.

Somme des nombres impairs

La somme des entiers impairs de 1 à 2n − 1 est un carré parfait ; plus précisément, elle vaut n². La preuve sans mots représentée à droite^[3] consiste à ajouter des bandes successives (ici, alternativement noires et blanches) formées d'un nombre impair de carreaux, pour obtenir une suite croissante de carrés, et ce indéfiniment.

Somme des puissances des entiers

Les formules donnant la somme des puissances n-èmes des entiers consécutifs (formules de Faulhaber) peuvent être démontrées visuellement pour n = 1, 2 ou 3 ; la jolie preuve visuelle ci-dessous^[4] illustre le fait que

$1+4+9+\dots+n^2=\frac{n(n+\frac12)(n+1)}{3}$;

elle demande cependant une observation plus attentive que la précédente pour être convaincante.

Les trois pyramides ont pour même volume la somme des carrés de 1 à n (n=4 dans cette illustration) ; le parallélépipède final est de côtés n, n+1 et n+1/2, d'où la formule de Faulhaber pour la somme des carrés.

Preuve sans mot de la formule $\scriptstyle\sum_{k=1}^n k^3=\sum_{k=1}^nk\times k^2=$$\scriptstyle\left(\sum_ {k=1}^nk\right)^2$

En revanche, la preuve visuelle ci-contre, proposée par Solomon W. Golomb, de ce que la somme des cubes des entiers de 1 à n est égale au carré de la somme de ces mêmes entiers, semble difficilement pouvoir se passer de quelques commentaires (expliquant par exemple que les k carrés additionnés dans chaque bande sont eux mêmes de côté k) ; Nelsen la considère cependant comme une preuve sans mots à part entière^[5].

Théorème de Pythagore

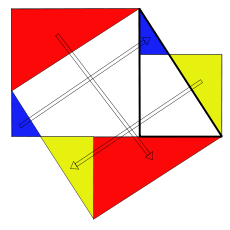
Une preuve sans mots du théorème de Pythagore, d'après le Zhou Bi Suan Jing (en).

Le théorème de Pythagore possède de nombreuses preuves sans mots^[6] ; celle de droite (adaptée du Zhou Bi Suan Jing (en), un recueil chinois d'avant l'ère chrétienne), si elle n'est pas la plus parlante, a le mérite d'être l'une des plus anciennes démonstrations connues de ce théorème, et repose sur deux calculs différents de l'aire du grand carré, donnant la célèbre relation entre les côtés a² + b² = c². Cette démonstration demande plus d'efforts au lecteur que les précédentes (il faut voir que les 4 triangles rectangles se replient vers l'intérieur du carré médian sans changer d'aire, puis utiliser l'identité a² + b² = (a − b)² + 2ab), mais est cependant considérée également par Nelsen comme un exemple de preuve sans mots^[7]. La figure ci-dessous est la reconstitution moderne (et animée) d'une version ultérieure^[8], ne demandant plus aucun calcul.

L'aire du rectangle (ab) ne peut dépasser la somme des aires correspondant à l'intégrale de la fonction f (en rouge) et de la fonction f ^{− 1} (en jaune)

Inégalité de Young

Le diagramme ci-contre donne une preuve graphique très simple de l'inégalité de Young, $ab \le \int_0^a f(x)dx + \int_0^b f^{-1}(y)dy$ (où f est une fonction continue croissante telle que f(0)=0), en interprétant les deux intégrales comme deux aires bordées par le graphe de f ; il permet même de montrer facilement que l'égalité entre les deux termes n'a lieu que si b=f(a).

Peut-on parler de démonstration ?

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue !

Les preuves sans mots constituent-elles des démonstrations au sens mathématique de ce terme ? La question mérite d'être posée, compte-tenu de résultats manifestement absurdes obtenus par des preuves visuelles, comme celles que l'on trouvera dans l'article paradoxe du carré manquant, et qui reposent souvent sur des illusions d'optique.

Elles constituent souvent, quand elles n'ont pas vocation à piéger un lecteur, une démonstration aisément accessible sans le bagage nécessaire à une démonstration rigoureuse.

Elles permettent de conjecturer un résultat, sans perdre de vue la nécessité de démontrer, puisqu'il s'agit, selon George Pólya, de « d'abord imaginer, ensuite prouver »^[9]

Annexes

Voir aussi

• Algèbre géométrique
• Paradoxe du carré manquant
• Sangaku (problème sans mots)

Bibliographie

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Proof without words » (voir la liste des auteurs)

• Jean-Paul Delahaye, Les preuves sans mots dans Pour la Science, février 1998.
• (en) Roger B. Nelsen, Proofs without Words : Exercises in Visual Thinking, Mathematical Association of America, 1993 (ISBN 978-0-88385-700-7).
• (en) Roger B. Nelsen, Proofs without Words II : More Exercises in Visual Thinking, Mathematical Association of America, 2000.
• (en) Claudi Alsina et Roger B. Nelsen, An Invitation to Proofs Without Words, European Journal of Pure and Applied Mathematics, 2010.

Notes et références

1. ↑ Voir l'entrée preuves sans mots (en) sur le site de MathWorld
2. ↑ William Dunham, The Mathematical Universe, p.120
3. ↑ William Dunham, The Mathematical Universe, p.121.
4. ↑ Elle provient de : Roger B. Nelsen Proofs without Words.
5. ↑ Roger B. Nelsen Proofs without Words
6. ↑ Roger B. Nelsen en recense une douzaine
7. ↑ Roger B. Nelsen Proofs without Words p. 3
8. ↑ Voir, à l'article Théorème de Pythagore, la section concernant le théorème de Gougu pour des informations plus précises
9. ↑ Alain Bouvier, La mystification mathématique, éd. Hermann, Paris, 1981, p.40

Liens externes

• Le site de Art of Problem Solving (en) contient un ensemble d'applets Java illustrant des preuves sans mots.
• On trouvera aussi de nombreux documents (en anglais) sur le site de Robert B. Nelsen.