Càdlàg

En mathématiques, une fonction càdlàg (continue à droite, limite à gauche) est une fonction définie sur un ensemble E de nombres réels qui est continue à droite en tout point de E et admet une limite à gauche tout point de E. Les fonctions càdlàg sont importantes dans l'étude des processus stochastiques qui sont notamment des processus à sauts. L'ensemble des fonctions càdlàg est appelé l'espace de Skorokhod.

Il est à noter que la notation càdlàg est utilisée internationalement. Il existe cependant la notation équivalente en anglais : RCLL (« right continuous with left limits »). Il existe également la notion de fonction càglàd (continue à gauche, limite à droite), qui est l'équivalent par une inversion gauche-droite.

Définition

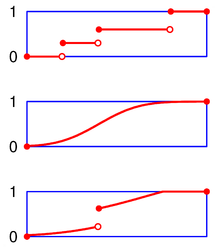Les fonctions de répartition sont des exemples de fonctions càdlàg.

Soient (M,d) un espace métrique et E ⊆ R un sous-ensemble de nombres réels. Une fonction ƒ: E → M est une fonction càdlàg si pour tout t ∈ E,

• la limite à gauche définie par ƒ(t−) := lim_s↑t ƒ(s):= lim_{s→t, s<t} ƒ(s) existe; et
• la limite à droite définie par ƒ(t+) := lim_s↓t ƒ(s):= lim_{s→t, s>t} ƒ(s) existe et est égale à ƒ(t).

La limite utilisée ici est celle définie par la métrique d.

Exemples

• Les fonctions continues sont des fonctions càdlàg.
• Les fonctions de répartition sont des fonctions càdlàg.
• les trajectoires d'un processus de Lévy sont des trajectoires càdlàg.

L'espace de Skorokhod

L'ensemble des fonctions càdlàg de E dans M est souvent noté D(E; M) et est appelé l'espace de Skorokhod en référence au mathématicien ukrainien Anatoliy Skorokhod. L'espace de Skorokhod peut être muni d'un topologie qui, intuitivement, permet de "tordre" un petit peu le temps et l'espace (alors que la topologie traditionnelle de la convergence uniforme permet de "tordre" l'espace un petit peu). Pour simplifier, restreignons-nous à E = [0, T] et M = Rⁿ (voir Billingsley pour des cas plus généraux).

Définissons d'abord un analogue, que l'on note ϖ′_ƒ(δ), du module de continuité. Pour tout sous-ensemble F ⊆ E, on pose

$w_{f} (F) := \sup_{s, t \in F} | f(s) - f(t) |$

et, pour δ > 0, définissons le module càdlàg par

$\varpi'_{f} (\delta) := \inf_{\Pi_\delta} \max_{1 \leq i \leq k} w_{f} ([t_{i - 1}, t_{i})),$

où l'infimum est pris sur l'ensemble des partitions Π_δ = {(t₀,t₁,...,t_k), tel que 0 = t₀ < t₁ < … < t_k = T, k ∈ N et min_i (t_i − t_i−1) > δ}. Cette définition reste valable pour des fonctions non-càdlàg (de même que le module de continuité usuel est valable pour les fonctions continues). On peut montrer que ƒ est càdlàg si et seulement si ϖ′_ƒ(δ) → 0 quand δ → 0.

Notons Λ l'ensemble des bijections continues strictement croissantes de E dans lui-même. notons

$\| f \| := \sup_{t \in E} | f(t) |$

la norme uniforme des fonctions sur E. Définissons la métrique de Skorokhod σ sur D(E; M) par

$\sigma (f, g) := \inf_{\lambda \in \Lambda} \max \{ \| \lambda - I \|, \| f - g \circ \lambda \| \},$

où I: E → E est la fonction identité. La notion intuitive de "tordue" en temps est mesurée par ||λ − I|| ; de même, ||ƒ − g○λ|| mesure la taille de la "torsion" en espace.

On peut montrer que cette métrique de Skorokhod est une vraie métrique. La topologie Σ engendrée par σ est appelée topologie de Skorokhod sur D(E; M).

Propriétés de l'espace de Skorokhod

Généralisation de la topologie uniforme

L'espace C(E,M) des fonctions continues de E dans M est un sous-espace de D(E,M). La topologie de Skorokhod relative à C(E,M) coïncide avec sa topologie uniforme.

Complétude

On peut montrer que, bien que D(E,M) ne soit pas un espace complet par rapport à la métrique de Skorokhod σ, il existe une métrique topologiquement équivalente σ₀ par rapport à laquelle D(E,M) est complet.

Séparabilité

Par rapport à σ ou σ₀ D(E,M) est un espace séparable. L'espace de Skorokhod est ainsi un espace polonais.

Tension dans l'espace de Skorokhod

Par une application du théorème d'Ascoli, on peut montrer qu'une suite (μ_n)_n=1,2,… de mesures de probabilité sur l'espace de Skorokhod est tendue (en) si et seulement si les deux conditions suivantes sont satisfaites :

$\lim_{a \to \infty} \limsup_{n \to \infty} \mu_{n}\big( \{ f \in D \;|\; \| f \| \geq a \} \big) = 0,$

et

$\lim_{\delta \to 0} \limsup_{n \to \infty} \mu_{n}\big( \{ f \in D \;|\; \varpi'_{f} (\delta) \geq \varepsilon \} \big) = 0\text{ pour tout }\varepsilon > 0.$.

Références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Càdlàg » (voir la liste des auteurs)
• (en) Billingsley, Patrick, Probability and Measure, New York, NY, John Wiley & Sons, Inc., 1995, 3^e éd. (ISBN 978-0-471-00710-4) (LCCN 94028500) 
• (en) Billingsley, Patrick, Convergence of Probability Measures, New York, NY, John Wiley & Sons, Inc., 1999, 2^e éd. (ISBN 978-0-471-19745-4) (LCCN 99030372)