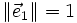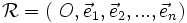Base orthonormée

Base orthonormale

Pour les articles homonymes, voir BON.

Une base orthonormale (BON) est une structure mathématique.

Définition

Soit E_n un espace vectoriel euclidien de dimension n, où n est un entier naturel non nul, et 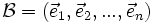$\mathcal B = ( \vec e_1 , \vec e_2 , ... , \vec e_n)$, une base de E_n.

• Si n = 1, alors 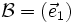$\mathcal B = ( \vec e_1)$ est dite orthonormale si et seulement si

$\| \vec e_1 \| = 1$

• Si n > 1, alors 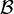$\mathcal B$ est orthonormale si et seulement si

$\| \vec e_1 \| = \| \vec e_2 \| = ... = \| \vec e_n \| = 1$

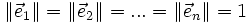
et,

pour tout 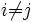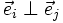$i \not = j$, $\vec e_i \perp \vec e_j$ ( c'est-à-dire 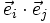$\vec e_i \cdot \vec e_j$ = 0 )

Une base orthonormale est donc une base où tous les vecteurs de la base sont de norme 1 et sont orthogonaux 2 à 2. Cette définition s'applique aussi sur un espace hermitien. Il correspond à une généralisation aux complexes d'un espace euclidien.

Repère orthonormal (ou orthonormé)

Soient A_n un espace affine euclidien associé à l'espace vectoriel euclidien E_n et O un point quelconque de A_n, alors le repère

$\mathcal R = (\ O , \vec e_1 , \vec e_2 , ... , \vec e_n)$

est dit orthonormal si et seulement si sa base associée 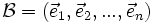$\mathcal B = ( \vec e_1 , \vec e_2 , ... , \vec e_n)$ est elle-même orthonormale.

En géométrie dans l'espace

En géométrie dans l'espace, la base est en général notée 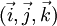$(\vec{i},\vec{j},\vec{k})$ au lieu de $(\vec{e_1},\vec{e_2},\vec{e_3})$.

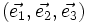La base est dite « directe » si 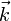$\vec{k}$ est le produit vectoriel de 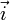$\vec{i}$ et de $\vec{j}$ ($\vec{k} = \vec{i} \wedge \vec{j}$).

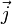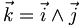Le terme « base orthonormale directe » est parfois abrégé par le sigle BOD.

Si la base associée à un repère est orthonormale directe, le repère est un repère orthonormal direct, terme parfois abrégé par le sigle ROND.

Voir l'article Orientation (mathématiques).

Orthonormalisation

Article détaillé : Procédé de Gram-Schmidt.

On peut à partir d'une base qui n'est pas orthonormale construire une base orthonormale. La méthode la plus répandue est l'orthogonalisation de Gram-Schmidt. Cette méthode permet de construire une base orthonormale à partir de toute base de l'espace.

Voir aussi

• Système de coordonnées cartésiennes
• Base canonique

Articles de mathématiques en rapport avec l'algèbre bilinéaire

Espace euclidien • Espace hermitien • Forme bilinéaire • Forme quadratique • Forme sesquilinéaire • Orthogonalité • Base orthonormale • Projection orthogonale • Inégalité de Cauchy-Schwarz • Inégalité de Minkowski • Matrice définie positive • Matrice semi-définie positive • Décomposition QR • Déterminant de Gram • Espace de Hilbert • Base de Hilbert • Théorème spectral • Théorème de Stampacchia • Théorème de Riesz • Théorème de Lax-Milgram • Théorème de représentation de Riesz

modifier

Ce document provient de « Base orthonormale ».