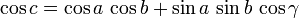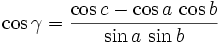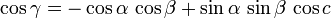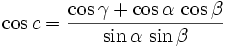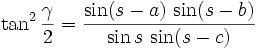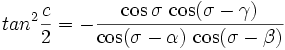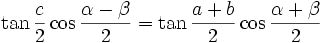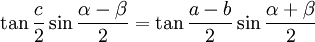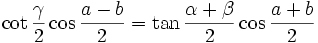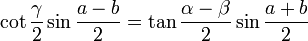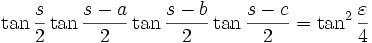- Trigonometrie spherique
-
Trigonométrie sphérique
La trigonométrie sphérique est un ensemble de relations analogues à celles de la trigonométrie euclidienne mais portant sur les angles et distances repérés sur une sphère.
Les règles habituelles de la trigonométrie euclidienne ne sont plus applicables ; par exemple la somme des angles d'un triangle situé sur une sphère est supérieure à 180 degrés et les segments de droites deviennent des arcs de grands cercles.
Sommaire
Le triangle sphérique
Formules premières
On considère trois points A, B et C sur une sphère comme représentés par la figure ci-contre, on note a la longueur (sur la surface de la sphère) du côté opposé au sommet A et α l'angle (toujours sur la surface de la sphère) du triangle en ce sommet, et de façon analogue pour les autres sommets. Les longueurs a, b et c seront en fait considérées comme des angles dans ce qui suit, à savoir les angles sous-tendus au centre de la sphère par la partie de grand cercle correspondante (par exemple, l'angle de 2π est la circonférence de la sphère).
La relation la plus importante de la trigonométrie sphérique est la suivante, qui relie la longueur d'un côté à celles de deux autres côtés ainsi que l'angle entre eux :
Cela se démontre par exemple en exprimant de plusieurs façons le produit scalaire, dans l'espace euclidien ambiant, entre les vecteurs reliant le centre O de la sphère aux points A et B. Dans le cas particulier où le triangle est rectangle en C, on obtient cosc = cosa cosb, formule analogue du théorème de Pythagore pour la trigonométrie sphérique. On peut remarquer notamment que si on développe le cosinus au deuxième ordre, c'est-à-dire si le triangle est suffisamment petit on retrouve effectivement le théorème de Pythagore. La formule ci-dessus permet également, si on considère deux points A et B sur la Terre et C le pôle nord, de calculer la distance entre A et B en fonction de leurs latitudes (complémentaires à a et b) et de la différence entre leurs longitudes (γ). La relation peut également s'écrire
qu'il ne faut pas confondre avec la relation duale (obtenue en remplaçant, dans la relation initiale, tous les grands cercles par leurs points polaires), soit
soit encore
On remarquera en particulier que d'après cette dernière formule, un triangle sphérique est déterminé par ses trois angles, ce qui est très différent du triangle euclidien (plan). Il y a une analogie parfaite (de dualité), dans le triangle sphérique, entre longueurs des côtés et angles aux sommets. Pour illustrer cette analogie, on peut d'ailleurs mentionner la formule des sinus,
- sina:sinb:sinc = sinα:sinβ:sinγ
ce qui doit se comprendre comme « les trois quantités de gauche sont dans les mêmes proportions que les trois quantités de droite (le rapport entre deux quelconques à gauche est le même que le rapport correspondant à droite) ».
Autres formules
Formules des demi-angles et demi-côtés
Soit s=½(a+b+c) le demi-périmètre du triangle. Alors on a
et pour les formules duales, si σ=½(α+β+γ) :
Formules de Gauss
On a
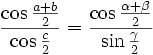 et
et 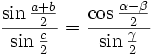 ainsi que
ainsi que 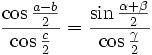 et
et 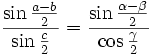
Analogies de Napier
Elles s'obtiennent en combinant deux à deux les formules de Gauss :
Aire du triangle sphérique
De façon remarquable, l'aire du triangle sphérique se calcule très simplement à partir de ses trois angles : elle est exactement égale à son « défaut d'euclidianité » (différence entre la somme des angles du triangle et π) multiplié par le carré du rayon R de la sphère.
- Soit :
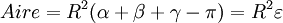
Remarque:ε est un angle solide s'exprimant en stéradians (pour α, β et γ exprimés en radians).
Formule de l'Huilier
Cette formule est analogue à la formule de Héron qui calcule l'aire d'un triangle euclidien en fonction de ses côtés, et elle fait la même chose pour le triangle sphérique :
(on rappelle qu'on a appelé s=(a+b+c)/2 le demi-périmètre).
Aperçu historique
La trigonométrie, et en particulier la trigonométrie sphérique doit beaucoup aux astronomes et mathématiciens grecs Hipparque de Nicée[1] ainsi que Ménélaüs d'Alexandrie, mais aussi aux mathématiciens persans de langue arabe et indiens. Parmi les plus célèbres figurent Al Biruni, Abu Nasr Mansur et Bhāskara II. Le premier traité de trigonométrie sphérique semble avoir été écrit vers 1060 par Al Jayyani, un mathématicien de l'Espagne islamique.
Applications
- Calculs de coordonnées :
- en astronomie, pour les changements relatifs aux divers systèmes de coordonnées angulaires : déclinaison, ascension droite, angle horaire, azimut et distance zénithale (ou hauteur) ;
- en géographie (latitude et longitude) ;
Voir aussi
Liens internes
- Ménélaüs d'Alexandrie - Al Biruni ~ Abu Nasr Mansur ~ Gauss ~ Napier
- Angle ~ Trigonométrie ~ Triangle ~ Résolution d'un triangle
- Géométrie non euclidienne
- Sphère ~ Grand cercle
Liens externes
- http://artemmis.univ-mrs.fr/cybermeca/Formcont/mecaspa/COURS_SA/TRIGOSPH/TrigoSph.htm
- http://astroti.free.fr/astroti/calc/astrosph.html
- http://www.eleves.ens.fr:8080/home/madore/math/carto.pdf
- Al Biruni et Abu Nasr Mansur
Notes et références
- ↑ Œuvres complètes de François Arago. François Arago, tome 3, page 158 (Gide, Paris - 1855).
- Portail de la géométrie
Catégorie : Trigonométrie
Wikimedia Foundation. 2010.