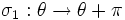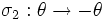- Transition d'obrifold
-
Orbifold
En mathématiques, un orbifold est une généralisation de la notion de variété[1] contenant de possibles singularités. Ces espaces ont été introduits explicitement pour la première fois par Satake en 1956 sous le nom de V-manifolds. Pour passer de la notion de variété (différentiable) à celle d'orbifold, on ajoute comme modèles locaux tous les quotients d'ouverts de Rn par l'action de groupes finis. L'intérêt pour ces objets a été ravivé considérablement à la fin des années 70 par William Thurston en lien avec sa conjecture de géométrisation.
En physique, ces espaces ont été considérés initialement comme espaces de compactification en théorie des cordes car malgré la présence de singularités la théorie y est bien définie.
Lorsqu'ils sont utilisés dans le cadre plus particulier de la théorie des supercordes, les orbifolds autorisés doivent avoir la propriété supplémentaire d'être des variétés de Calabi-Yau afin de préserver une quantité minimale de supersymétrie. Mais dans le cas où des singularités sont présentes, il s'agit là d'une extension de la définition originale des espaces de Calabi-Yau car ceux-ci sont en principe des espaces sans singularité.Sommaire
Orbifolds en topologie différentielle et en géométrie
Définition
Un orbifold (sans bord) O est un espace métrique muni d'un atlas orbifold, c’est-à-dire d'un ensemble de quadruplets
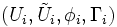 où Ui est un ouvert de O,
où Ui est un ouvert de O, 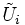 est un ouvert de Rn, Γi est un groupe fini agissant de façon lisse sur
est un ouvert de Rn, Γi est un groupe fini agissant de façon lisse sur 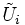 et φi est une application continue qui descend en homéomorphisme de
et φi est une application continue qui descend en homéomorphisme de 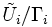 dans Ui. L'ensemble de ces quadruplets doit vérifier :
dans Ui. L'ensemble de ces quadruplets doit vérifier :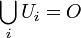 ,
,- si
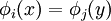 alors il existe des voisinages
alors il existe des voisinages 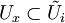 et
et 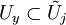 de x et y et un difféomorphisme
de x et y et un difféomorphisme 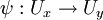 tel que
tel que 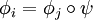 .
.
Chaque quadruplet d'un atlas est appelé carte de O. Deux atlas définissent la même structure d'orbifold si leur réunion est encore un atlas. Lorsqu'il y a un risque de confusion, on notera | O | l'espace topologique sous-jacent à un orbifold O.
Un point ne possédant pas de carte pour lequel le groupe agissant est trivial est dit singulier ou exceptionnel.
Une application lisse entre deux orbifolds O et O' est une fonction continue
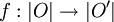 telle que pour tout point x de O il existe des cartes
telle que pour tout point x de O il existe des cartes 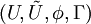 et
et 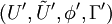 où
où 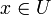 et
et 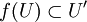 et une application lisse
et une application lisse 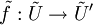 au dessus de f qui soit équivariante par rapport à un certain homomorphisme de Γ dans Γ'. Une telle application est appelé immersion ou submersion si tous les
au dessus de f qui soit équivariante par rapport à un certain homomorphisme de Γ dans Γ'. Une telle application est appelé immersion ou submersion si tous les 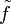 le sont. Une immersion qui est un homéomorphisme sur son image est appelé un plongement. Un difféomorphisme est un plongement surjectif.
le sont. Une immersion qui est un homéomorphisme sur son image est appelé un plongement. Un difféomorphisme est un plongement surjectif.Exemples simples
On construit la plupart du temps un orbifold comme espace quotient d'une variété (sans singularité) par une symétrie discrète de celle-ci. Si l'opération de symétrie ne possède pas de point fixe alors on sait que le résultat est encore une variété, mais si par contre il existe un ou plusieurs points fixes alors le quotient possède des singularités sur chacun de ceux-ci et est donc « véritablement » un orbifold.
Par exemple si on considère un cercle
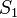 de rayon
de rayon 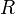 qui est une variété (de dimension 1) et qu'on le paramétrise par un angle
qui est une variété (de dimension 1) et qu'on le paramétrise par un angle ![\theta\in
[0;2\pi]\,](/pictures/frwiki/55/7b5135293d4faf7e84b821e8ca18e5da.png) alors on peut considérer les deux opérations suivantes
alors on peut considérer les deux opérations suivantesAlors
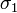 , qui est une translation d'une demi-période, ne possède pas de point fixe. Le quotient associé, noté S1 / σ1 est donc encore une variété et de fait il s'agit encore d'un cercle mais de rayon
, qui est une translation d'une demi-période, ne possède pas de point fixe. Le quotient associé, noté S1 / σ1 est donc encore une variété et de fait il s'agit encore d'un cercle mais de rayon 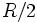 .
.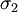 par contre possède deux points fixe en
par contre possède deux points fixe en 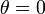 et
et 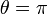 .
. 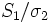 n'est donc pas une variété mais bien un orbifold. Il est topologiquement équivalent à un segment
n'est donc pas une variété mais bien un orbifold. Il est topologiquement équivalent à un segment ![[0;\pi ]\,](/pictures/frwiki/101/eab9fbf9a934a4fb17c30c5907b92d79.png) et est singulier aux deux extrémités.
et est singulier aux deux extrémités.En dimension 2, l'exemple le plus simple est celui du quotient d'un disque ouvert par l'action d'une rotation. Le résultat est topologiquement un disque mais sa structure d'orbifold comprend un point singulier dont le groupe est cyclique (la singularité est dite conique).
Le premier exemple de surface orbifold qui n'est pas le quotient d'une variété lisse est obtenue en recollant l'exemple précédent et un disque lisse pour obtenir une sphère ayant un point exceptionnel conique.
Revêtements et groupe fondamental
Les orbifolds étant introduits en particulier pour donner une structure au quotient d'une variété par l'action d'un groupe fini, on veut pouvoir dire que si M est une variété sur laquelle agit un groupe fini G alors l'application
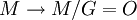 est un revêtement et que si M est simplement connexe alors l'orbifold quotient a pour groupe fondamental G.
est un revêtement et que si M est simplement connexe alors l'orbifold quotient a pour groupe fondamental G.Revêtements
Un revêtement d'un orbifold O par un orbifold
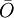 est une application continue
est une application continue 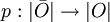 telle que tout point x de O admette un voisinage U vérifiant : chaque composante connexe V de p − 1(U) admet une carte
telle que tout point x de O admette un voisinage U vérifiant : chaque composante connexe V de p − 1(U) admet une carte 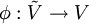 telle que
telle que 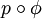 soit une carte de O.
soit une carte de O.Il faut prendre garde au fait que l'application p n'est en général pas un revêtement entre espace topologiques.
On appelle revêtement universel de O un revêtement
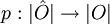 tel que pour tout revêtement
tel que pour tout revêtement 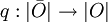 il existe un revêtement
il existe un revêtement 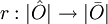 tel que
tel que 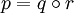 . D'après un théorème de Thurston, tout orbifold possède un revêtement universel qui est unique à difféomorphisme près.
. D'après un théorème de Thurston, tout orbifold possède un revêtement universel qui est unique à difféomorphisme près.Groupe fondamental
Le groupe fondamental d'un orbifold est le groupe des automorphismes de son revêtement universel, c’est-à-dire des difféomorphismes de
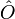 tels que
tels que 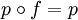 . On le note π1(O) et on a bien
. On le note π1(O) et on a bien 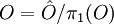 .
.Lien avec la géométrisation de Thurston
La conjecture de géométrisation de Thurston affirme, grossièrement, que toute variété compacte orientable de dimension trois peut être découpée en un nombre fini de morceaux portant une structure géométrique. Dans le cas où la variété admet une action non-libre d'un groupe fini, il suffit de munir l'orbifold quotient d'une structure géométrique puis de remonter celle-ci sur la variété de départ. C'est pourquoi il était important de comprendre les orbifolds car, paradoxalement, il est plus facile de munir un orbifold (non-lisse) d'une structure géométrique que de le faire pour une variété lisse générale.
Par ailleurs les orbifolds de dimension deux peuvent jouer le rôle de bases de fibrés en cercles appelés fibrés de Seifert et qui jouent un rôle important comme morceaux de la décomposition de Thurston (la définition d'un fibré au dessus d'un orbifold est adaptée de celle concernant les variétés par une démarche proche de celle utilisée plus haut pour les revêtements).
Applications à la théorie des cordes
Lien avec les espaces de Calabi-Yau
Article détaillé : Variété de Calabi-Yau.Lorsqu'en théorie des supercordes on cherche à construire des modèles phénoménologiques réalistes, il est nécessaire d'effectuer une réduction dimensionnelle car les supercordes se propagent naturellement dans un espace à 10 dimensions alors que l'espace-temps de l'univers observable a seulement 4 dimensions apparentes. Les contraintes formelles de la théorie imposent néanmoins des restrictions sur l'espace de compactification dans lequel sont cachées les dimensions supplémentaires. Dans le cas où on cherche un modèle réaliste en 4 dimensions qui possède la supersymétrie[2] alors l'espace de compactification doit être un espace de Calabi-Yau possédant donc 6 dimensions.
Il existe d'innombrables possibilités de Calabi-Yau différentes (des dizaines de milliers, en fait). Leur étude générale est mathématiquement très complexe et pendant longtemps il a été difficile d'en construire beaucoup explicitement. Les orbifolds sont alors très utiles car lorsqu'ils satisfont aux contraintes imposées par la supersymétrie que nous avons mentionnées alors ils constituent des exemples de Calabi-Yau dégénérés, du fait de la présence de singularités, mais néanmoins tout à fait acceptables du point de vue de la théorie physique. De tels orbifolds sont alors dits supersymétriques. L'avantage de considérer des orbifolds supersymétriques plutôt que des Calabi-Yau généraux est que leur construction est dans la pratique beaucoup plus simple d'un point de vue purement technique.
Il est alors très souvent possible, comme on va le voir ci-dessous, de relier un obifold supersymétrique possédant des singularités à une famille continue d'espaces de Calabi-Yau sans singularité.
Cas de
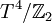 et K3
et K3L'espace K3 possède 16 cycles de dimension 2 qui sont topologiquement équivalents à des sphères usuelles. Si on fait tendre la surface de ces sphères vers 0 alors K3 développe 16 singularités (cette limite se trouve au bord de l'espace de modules de cette variété). C'est à cette limite singulière que correspond l'orbifold
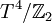 obtenu en quotientant le 4-tore par la symétrie d'inversion de chacune des coordonnées (c'est-à-dire
obtenu en quotientant le 4-tore par la symétrie d'inversion de chacune des coordonnées (c'est-à-dire 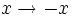 dans chaque direction).
dans chaque direction).Symétrie miroir
Article détaillé : symétrie miroir.La symétrie miroir est un concept dont l'idée fut créée en 1988. Elle dit que deux espace de Calabi-Yau conduisent à la même physique si leur nombre de trous total dans toutes les dimensions sont égaux. Cela veut dire que même si leur nombre de trous n'est pas égal par dimensions, ils conduisent à la même physique si leur nombre de trous total est identique. J'entends par même physique, que des Calabi-Yau avec les mêmes nombres de trous au total conduit à un univers avec le même nombre de famille.
Opération
Cette technique fut inventée dans les années 80 par Dixon, Vafa, Witten et Harvey. L'opération d'orbifold consiste à créer une nouvelle forme de Calabi-Yau en reliant différents points du Calabi-Yau initial. C'est une méthode pour manipuler mathématiquement des espaces de Calabi-Yau en reliant certains de ces points. Mais ces manipulations sont si compliquées que les physiciens n'ont pas envisagé de la reproduire sur une forme aussi compliquée qu'un espace de Calabi-Yau dans toute sa splendeur.
L'opération d'orbifold n'est pas une transition géométrique comme la transition de flop ou la transition de conifold qui provoque des cataclysmes monstrueux comme des déchirures de l'espace-temps.
Conséquences
En identifiant ainsi certains points, l'espace de Calabi-Yau de « départ » (que nous appellerons α) et celui d'« arrivée » (que nous appellerons β) différent par leur nombre de trous dans chaque dimension : les trous des dimensions paires (2e, 4e, 6e dimension) de Calabi-Yau β était égaux au nombre de trous dans les dimensions impaires (1ère, 3e, 5e) du Calabi-Yau α et vice-versa ! Mais cela revient à dire que le nombre de trous total ne change pas. Mais cette inversion pair avec impair aboutit à des structures géométriques fort distinctes.
Voir aussi
Notes
- ↑ le mot d'origine anglaise est une variation de manifold qui est la traduction de variété.
- ↑ Cette hypothèse de l'existence de la supersymétrie dans les domaines de haute énergie, c'est-à-dire au delà d'une échelle comprise entre
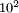 et
et 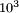 GeV environ, alors qu'elle serait brisée à nos échelles courantes, c'est-à-dire en dessous de l'échelle électrofaible soit environ
GeV environ, alors qu'elle serait brisée à nos échelles courantes, c'est-à-dire en dessous de l'échelle électrofaible soit environ 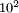 GeV, devrait être vérifiée dans le cadre des expérimentations qui seront effectuées au LHC, mis en service en 2008.
GeV, devrait être vérifiée dans le cadre des expérimentations qui seront effectuées au LHC, mis en service en 2008.
- Portail de la physique
- Portail des mathématiques
- Portail de la géométrie
Catégories : Théorie des cordes | Topologie différentielle
Wikimedia Foundation. 2010.