- Axiomes de plans projectifs/homogènes
-
Axiomes de plans projectifs/homogènes
Article principal : Axiomes de plans projectifs.« Faire des mathématiques, c’est donner le même nom à des choses différentes. » Henri Poincaré
Le plan homogène est une création abstraite de géométrie analytique destinée à uniformiser les calculs d'intersections de droites sans se préoccuper de savoir si elles sont parallèles ou non. Dans un premier temps le plan homogène et les coordonnées homogènes ont un but simplement computationnel. Dans un deuxième temps si on approfondit les conséquences de la définition des coordonnées homogènes on s'aperçoit que ceci correspond à la définition d'un plan projectif; comme il existe plusieurs sortes de plans projectifs, on se demande duquel il s'agit et l'on peut démontrer que le plan projectif homogène répond au théorème fondamental de la géométrie projective.
Cascade d'axiomes de plans projectifs
Plan projectif-tout-court
Un plan projectif (PP) est un ensemble de points et de droites (c'est-à-dire de groupements de points qu'on appellera droites). Un point est incident à cette droite s’il appartient à ce groupement. Une droite est incidente à un point si ce point fait partie de ce groupement. On dit aussi que cette droite passe par ce point ou que ce point est sur cette droite. Ce ne sont là que des questions de vocabulaire. Attention, une droite ne ressemble pas forcément aux bonnes vieilles droites de notre plan euclidien « naturel », ce n'est qu'un mot pour désigner des sous-ensembles de points. Une convention dans le dessin des figures, surtout lorsqu'elles dépassent le bord de page, est de « courber les droites ».
Plan projectif d'incidence (la base minimaliste)
Un plan projectif (PPI) d’incidence est un PP qui vérifie les axiomes :
- Il existe au moins 2 points et une droite.
- Chaque droite possède au moins 3 points.
- Pour deux points distincts il existe une et une seule droite qui leur est incidente.
- Deux droites distinctes ont un et un seul point commun.
- Pour toute droite il existe au moins un point non incident à cette droite.
Plan projectif homogène
définition du plan projectif homogène
La géométrie projective homogène est la conception purement abstraite d'une structure ensembliste fondée sur des notions très élémentaires de théorie des ensembles. Le point de départ est un corps commutatif K dans lequel on exploite en particulier les propriétés d'associativité a*(b*c)=(a*b)*c, commutativité a*b=b*a et a+b=b+a, distributivité r*(a+b)=r*a+r*b, simplification d'une égalité ( r*a=r*b et r non nul impliquent a=b), toutes choses bien connues des lycéens. On invente une relation d'équivalence R très simple. A partir de là on étudie l'ensemble-quotient induit par cette relation d'équivalence, ce qui est un peu plus abstrait. Sur ces bases simples sera défini un plan projectif homogène (PPH) dont on verra ci-dessous qu'il est un cas particulier de plan projectif fondamental.
Un plan projectif homogène (PPH) est l'ensemble-quotient d'un ensemble E par une relation d'équivalence R,
- l'ensemble E étant un espace vectoriel de dimension 3 sur un corps commutatif K, privé du vecteur nul (0,0,0).
- la relation R étant telle que, si k est un élément non-nul de K et V et W sont deux vecteurs non-nuls de E, alors W = kV.
- On appelle "point" une des classes d'équivalence, représentée par (x,y,z).
- On appelle "droite" une des classes d'équivalence, représentée par (a,b,c).
- Un "point" et une "droite" sont incidents lorsque ax+by+cz=0.
- Ces coordonnées sont appelées coordonnées homogènes.
- Attention, le corps commutatif K est arbitraire : ce peut être celui des réels, celui des complexes, un corps fini tel que {0,1} ou {0,1,2}, etc.
- De plus, on pourra utilement « prolonger » le corps commutatif K jusqu'à l'infini, obtenant ainsi le corps prolongé P(K). Pour ce faire, les notations deviennent une peu lourdes. P(K) est bâti à partir de l'ensemble des doublets (c1,c2), c1 et c2 appartenant à K. Deux doublets (c1,c2), (c3,c4) sont équivalents lorsqu'il existe un élément c5 non-nul de K tel que c3=c5*c1 et c4=c5*c2. Cette relation d'équivalence induit un ensemble-quotient, c'est cet ensemble-quotient que l'on appelle le corps prolongé P(K). En termes concrets, si c2 est non-nul, l'élément (c1,c2) correspond au nombre c1/c2 de K ; si c2 est nul, l'élément (c1,0) est le « nombre-infini », noté ∞, qui est unique et ne correspond à rien dans K. Ouf ! Exemples : le nombre (10,5) correspond au classique nombre 2 de K, le nombre (10i,10) correspond au classique nombre i de K si celui-ci est l'ensemble des complexes, le nombre (30+20i,10i) correspond au nombre 2-3i de K si celui-ci est l'ensemble des complexes, et dans tous les cas, (p,0) est l'infini. Les lois de composition internes sont évidentes, à savoir l'addition (c1,c2)+(c3,c4)=(c1*c4+c2*c3, c2*c4) et la multiplication (c1,c2)*(c3,c4)=(c1*c3,c2*c4); l'opposé de (a,b) est (-a,b); l'inverse de (a,b) est (b,a). Les ajouts de lois de composition internes par rapport à K sont simplement que :
- ∞+(c3,c4)=(c1,0)+(c3,c4)=(1, 0)=∞ : l'infini est absorbant pour l'addition ;
- l'opposé de l'infini n'existe pas ;
- si c3 est non-nul, ∞*(c3,c4)=(c1,0)*(c3,c4)=(c1*c3, 0)=∞ ; l'infini est absorbant pour la multiplication, de même que zero ;
- ∞*0 n'est pas défini, car deux éléments absorbants ne peuvent pas se combiner ;
- on définit l'inverse de l'infini=(1,0) comme étant zéro=(0,1) et réciproquement, afin de prolonger la règle qui dit que l'inverse de (a,b) vaut (b,a) si a et b sont tous deux non-nuls.
- Cet ensemble prolongé servira au rapport anharmonique.
Tolérance d'écriture lorsqu'il n'y a pas d'ambiguïté et qu'on est sûr de ne pas avoir affaire à l'infini, on écrit souvent « c » au lieu de « (c,1) » ; mais il faut être prudent.
« Lorsque nous lisons actuellement des manuels de géométrie projective d'un formalisme absolu, sans figure, nous pensons que les étudiants ne peuvent, faute de formation adéquate, en comprendre la substance. » - Anne Boyé, Pour la science, n°21, novembre 2004-février 2005.
le Pp homogène est d'incidence
On peut vérifier que cet ensemble-quotient est bien un plan projectif d'incidence.
cet ensemble est bien un PPd'incidenceFichier:.PNG
- Il existe au moins 2 points. En effet on peut exhiber au moins les deux points (1,0,0) et (0,1,0), car le corps commutatif K contient au moins les 2 nombres 1 et 0.
- Chaque droite possède au moins 3 points. Soit la droite (a,b,c), a,b et c n'étant pas nuls les 3 points (b,-a,0), (0,c,-b) et (-c,0,a) existent, sont distincts et sont incidents à la droite. Si a est nul mais ni b ni c, la droite est (0,b,c) et on considère
les points (1,0,0) (0,c,-b) et (k(b-c),c,-b) qui possèdent les bonnes propriétés. Si a et b sont nuls, la droite est (0,0,1) qui contient les 3 points distincts (1,0,0) (0,1,0) (1,1,0).
- Pour deux points distincts il existe une et une seule droite qui leur est incidente. Soit les deux points (x,y,z) (t,u,v) distincts si xyz ne sont pas proportionnels à tuv, on cherche la ou les droites (a,b,c) qui leur sont incidentes. Cela conduit au système de deux équations ax+by+cz=0 et at+bu+cv=0 qui admet comme solutions l'ensemble des droites représentées par les vecteurs k*(yv-zu, zt-xv, xu-yt) qui font partie de la même classe d'équivalence, donc c'est une seule droite.
- Deux droites distinctes ont un et un seul point commun. Même démonstration en échangeant les rôles.
- Pour toute droite il existe au moins un point non incident à cette droite. Soit la droite (a,b,c). Si c est non-nul le point (c²,0,1-ac) existe et n'est pas sur la droite car le produit scalaire est=c. Si c est nul et pas a ni b, la droite est (a,b,0) et le point (1,0,0) convient. Si b et c sont nuls, la droite est (1,0,0) et le point (1,0,0) convient aussi.
- Donc les axiomes du PPI sont satisfaits par un PPH.
nombreuses propriétés du Pp homogène
Des recettes de cuisine pour les formulesEn matière de coordonnées homogènes l'usage est de garder Z dans (X;Y;Z), même si on sait que le point est affine et qu'on pourrait parler de (x,y,1). Pourquoi? simplement pour garder toutes les formules d'un degré homogène en X Y Z, même et surtout si ce degré est élevé, 4 ou 6 voir plus si affinités.
- Dans certains calculs compliqués, mettre en évidence des fonctions symétriques de X Y Z, quitte à avoir l'impression que ceci alourdit. Ceci peut indiquer une piste; par exemple la formule f=(u²+mm')*(m-m') est peut-être plus intéressante au carré f²=(u²+mm')*( (m+m')²-4mm') la différence a disparu, il ne reste plus que la somme et le produit qui sont symétriques, l'inconvénient étant qu'on a doublé le degré, et perdu le signe de f (qui nous est quelquefois indifférent).
- Penser à reconnaître un déterminant 3x3, un produit scalaire derrière une formule compliquée mais qui a des petits airs symétriques.
- Dans le même ordre d'idées tenter une écriture tensorielle, appliquer éventuellement l'associativité du produit tensoriel.
La plupart des propriétés analytiques des plans projectifs homogènes découlent de l'espace vectoriel de départ. Elles se réfèrent à des propriétés d'algèbre linéaire, de forme linéaire, de forme bilinéaire et de forme quadratique.
Quelques propriétés ANALYTIQUES intéressantes d'un PPHFichier:.PNG Les formules utilisent les propriétés du corps commutatif K.
-
- Un point est représenté par, à un facteur multiplicatif près,
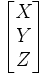
- Une droite est représentée par, à un facteur multiplicatif près,
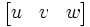
- L'incidence est représentée par :
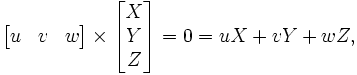 formule typiquement autoduale.
formule typiquement autoduale. - L'alignement de trois points P1, P2, P3 respectivement
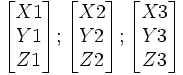 s'exprime par: det(P1,P2,P3) =
s'exprime par: det(P1,P2,P3) = 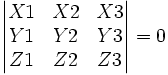
- La convergence de trois droites s'exprime par la même propriété de déterminant nul.
- Une bidroite [Bd] est représentée par une matrice 3x3 symétrique de déterminant nul. C'est l'ensemble des points P tels que: P*[Bd] *P=0. En fait c'est une conique ponctuelle dégénérée.
- Etant donné un quadruplet (ordonné) formé de 2 droites et de deux points (d1,d2,p3,p4), on appelle leur rapport anharmonique un nombre appartenant au prolongé de K. Ce nombre est défini ainsi : rho = birapport(d1 , d2, p3, p4), soit en termes mathématiques
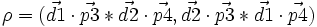 =(si le deuxième terme est non nul)
=(si le deuxième terme est non nul) 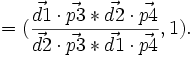
- Deux droites et deux points sont dits en division harmonique si leur rapport anharmonique est égal à (k, − k), k étant un élément non nul du corps K.
- Une transformation ponctuelle projective générale est représentée à un facteur multiplicatif près, par une matrice :
![[T]=\begin{bmatrix} t11 & t12 & t13 \\ t21& t22 & t23 \\ t31 & t32 & t33 \end{bmatrix} .](/pictures/frwiki/48/07bca9d3398b9965fd98e5a768f0f150.png) Elle est bijective si le déterminent est non-nul. La propriété fondamentale d'une telle transformation est la conservation des alignements. L'ensemble des transformations ponctuelles possède une loi de composition interne, le produit dont l'élément neutre est la transformation identité. Le produit est associatif et en général non-commutatif.
Elle est bijective si le déterminent est non-nul. La propriété fondamentale d'une telle transformation est la conservation des alignements. L'ensemble des transformations ponctuelles possède une loi de composition interne, le produit dont l'élément neutre est la transformation identité. Le produit est associatif et en général non-commutatif. - Une transformation ponctuelle homologie (généralisation de l'homothétie) est:
![[T]=\begin{bmatrix} a(ue+vf+wg) + bue& bve & bwe \\ buf& a(ue+vf+wg) +bvf & bwf \\ bug & bvg & a(ue+vf+wg) + bwg\end{bmatrix} .](/pictures/frwiki/101/ef8f05526dcfb80854f43cd8286de737.png) . La droite d=[u,v,w] est appelée axe de l'homologie, le point C=[e,f,g] est appelé son centre. L'axe et le centre ne sont pas incidents, les coefficients a et b n'ont pas leur somme nulle. Chaque point de l'axe est invariant, le centre est invariant. Si P'=T(P) est l'image de P, alors les points C P P' sont alignés. Si P' et Q' sont les transformés de P et Q, alors les droites (PQ) et (P'Q') se coupent sur l'axe.
. La droite d=[u,v,w] est appelée axe de l'homologie, le point C=[e,f,g] est appelé son centre. L'axe et le centre ne sont pas incidents, les coefficients a et b n'ont pas leur somme nulle. Chaque point de l'axe est invariant, le centre est invariant. Si P'=T(P) est l'image de P, alors les points C P P' sont alignés. Si P' et Q' sont les transformés de P et Q, alors les droites (PQ) et (P'Q') se coupent sur l'axe. - Une transformation ponctuelle homologie harmonique (généralisation de la symétrie par rapport à une droite) est obtenue lorsque b=-2a:
![[H]=\begin{bmatrix} a(-ue+vf+wg) & -2a ve & -2a we \\ -2a uf& a(ue-vf+wg) & -2a wf \\ -2a ug & -2a vg & a(ue+vf-wg)\end{bmatrix} .](/pictures/frwiki/50/241918b9bea2915c999f2fe39cd4e3fc.png) . Sa principale propriété est l'involutivité: H² = I involution. Son caractère harmonique se manifeste lorsqu'on calcule le rapport anharmonique de d,h, P et P', d étant l'axe, P étant un point, P' son image, h étant une droite qui contient le centre C et pas P. Ce birapport est alors équivalent à (1,-1). En effet, on peut le simplifier en remplaçant P' par H*P:
. Sa principale propriété est l'involutivité: H² = I involution. Son caractère harmonique se manifeste lorsqu'on calcule le rapport anharmonique de d,h, P et P', d étant l'axe, P étant un point, P' son image, h étant une droite qui contient le centre C et pas P. Ce birapport est alors équivalent à (1,-1). En effet, on peut le simplifier en remplaçant P' par H*P:
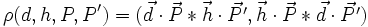
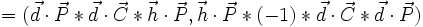
- La transformation homologie, lorsque a+b=0, dégénère en la projection sur l'axe à partir du centre.
- Etant donnés une droite d=[u,v,w] incidente à un point C=[e,f,g] appelés axe et centre, ainsi que deux nombres (a^3 et b) du corps K, une transformation ponctuelle [E] élation (généralisation de la translation) est:
![[E]=\begin{bmatrix} a^3 + bue& bve & bwe \\ buf& a^3 +bvf & bwf \\ bug & bvg & a^3 + bwg\end{bmatrix} .](/pictures/frwiki/55/75cbb7bf412164c079a754d6216859c8.png)
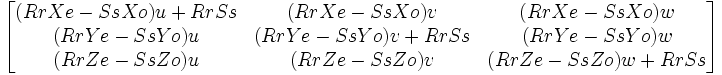
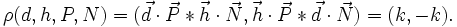
- Les élations et les homologies forment un ensemble de transformations appelées "dilatations" du plan projectif.
- Une conique ponctuelle définie à un facteur multiplicatif près, par une matrice [a]3*3 symétrique, est l'ensemble des points [X:Y:Z]définis par l'équation
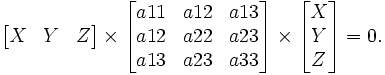
- Une conique tangentielle définie à un facteur multiplicatif près, par une matrice [d]3*3 symétrique, est l'ensemble des droites (u; v; w ) définies par l'équation

- La polaire d'un point [X:Y:Z] par rapport à une conique ponctuelle est la droite [U:V:W] définie à un facteur multiplicatif près:
![[U:V:W] =\begin{bmatrix}X& Y& Z\end{bmatrix} \times \begin{bmatrix} a11 & a12 & a13 \\ a12& a22 & a23 \\ a13 & a23 & a33 \end{bmatrix} .](/pictures/frwiki/48/0aac1f806aa8ac36a104e224cb99b714.png)
- La tangente en un de ses points [X:Y:Z] à une conique ponctuelle est la droite définie à un facteur multiplicatif près par les équations:
 et
et ![[U:V:W] =\begin{bmatrix}X& Y& Z\end{bmatrix} \times \begin{bmatrix} a11 & a12 & a13 \\ a12& a22 & a23 \\ a13 & a23 & a33 \end{bmatrix} .](/pictures/frwiki/48/0aac1f806aa8ac36a104e224cb99b714.png)
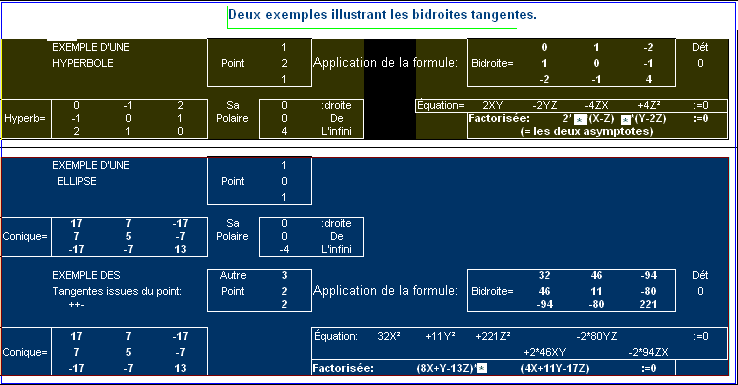
- Les deux tangentes à une conique
![[A]= \begin{bmatrix} a11 & a12 & a13 \\ a12& a22 & a23 \\ a13 & a23 & a33 \end{bmatrix}](/pictures/frwiki/52/4e3f070cc823cec08f949e149c2c2bfa.png) ponctuelle issues d'un point [x0 :y0 :z0] sont représentées indistinctement par la bidroite définie ainsi. La polaire du point [x0 :y0 :z0 ] par rapport à la conique est la droite [u0 :v0 :w0 ],
ponctuelle issues d'un point [x0 :y0 :z0] sont représentées indistinctement par la bidroite définie ainsi. La polaire du point [x0 :y0 :z0 ] par rapport à la conique est la droite [u0 :v0 :w0 ], ![[ u0 :v0 :w0] = \begin{bmatrix}x0& y0& z0\end{bmatrix} \times \begin{bmatrix} a11 & a12 & a13 \\ a12& a22 & a23 \\ a13 & a23 & a33 \end{bmatrix}](/pictures/frwiki/53/587f8b86ec47818c1b1d86d5f4d08954.png) . La bidroite est représentée à un facteur multiplicatif près par la matrice symétrique 3x3 ,
. La bidroite est représentée à un facteur multiplicatif près par la matrice symétrique 3x3 ,
- Un point est représenté par, à un facteur multiplicatif près,
-
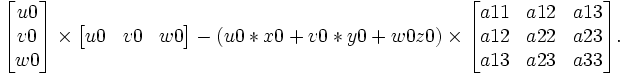
![= [A] \times \begin{bmatrix}x0\\ y0\\ z0\end{bmatrix} \times\begin{bmatrix}x0& y0& z0\end{bmatrix} \times [A]](/pictures/frwiki/55/79688bdf2e371f171da313ada2476a49.png)
![- \begin{bmatrix}x0& y0& z0\end{bmatrix} \times [A] \times \begin{bmatrix}x0\\ y0\\ z0\end{bmatrix} \times [A] .](/pictures/frwiki/52/4005aa6ab23d1965c6b2ee86b729e847.png) Cette formule ne préjuge en rien de l'existence ou non de tangentes réelles, d'ailleurs on ne précise pas dans quel corps commutatif K on travaille.
Cette formule ne préjuge en rien de l'existence ou non de tangentes réelles, d'ailleurs on ne précise pas dans quel corps commutatif K on travaille.
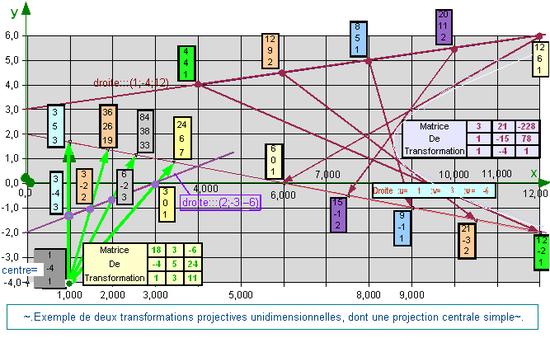
Formules de transformations unidimensionnelles dans un PPHIl sera intéressant pour la démonstration de théorèmes ultérieurs de disposer de la caractérisation de certaines transformations d'un point en un autre point, en particulier la transformation projective unidimensionnelle bijective d'une division rectiligne sur une autre droite ou sur elle-même. Soient la droite de départ= (u' , v', w') et la droite d'arrivée= (u , v, w). Une transformation projective est linéaire, donc représentée par une matrice carrée. Les points d'arrivée sont tous sur la droite d'arrivée SSI les lignes de cette matrice sont liées par u*ligne1+ v*ligne2+ w*ligne3 =0, son déterminant est nul, c'est naturel puisqu'il ne s'agit pas d'une bijection en dim2 mais seulement en dim1. Il reste 6 degrés de liberté à cette matrice, à un coefficient multiplicatif près; nous choisirons 6 paramètres a b c a' b' c' du corps des complexes, et définirons la matrice de transformation (T) d'une manière esthétique en équilibrant la combinaison linéaire des lignes par les éléments diagonaux:
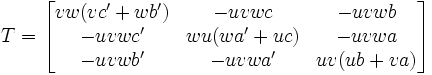 .
.
- Voilà deux transfos dont la droite d'arrivée est (u;v;w) = ( 1 ; 3 ; -6 ), la première avec a=24 b=-6 c=3 a'=3 b'=1 c'=-4, la matrice après simplification est
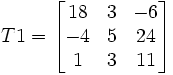 , on remarque qu'il s'agit d'une projection centrale simple à partir du point (1; -4; 1), on pourra vérifier que les birapports sont conservés. La seconde transformation, de droite de départ ( 1 ; -4 ; 12) et munie des paramètres a=78 b=-228 c=21 a'=-4 b'=1 c'=1, a pour matrice
, on remarque qu'il s'agit d'une projection centrale simple à partir du point (1; -4; 1), on pourra vérifier que les birapports sont conservés. La seconde transformation, de droite de départ ( 1 ; -4 ; 12) et munie des paramètres a=78 b=-228 c=21 a'=-4 b'=1 c'=1, a pour matrice 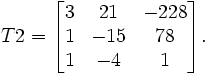 Les droites joignant un point à son image ne sont pas concourantes, on peut démontrer qu'elles sont tangentes à une conique, une parabole en l'occurrence car une de ces tangentes est la droite de l'infini.
Les droites joignant un point à son image ne sont pas concourantes, on peut démontrer qu'elles sont tangentes à une conique, une parabole en l'occurrence car une de ces tangentes est la droite de l'infini.-
- La transformation projective unidimensionnelle IDENTITE, ou "neutre" (N) de la droite (u; v; w) sur elle-même ne s'exprime pas par une matrice diagonale de 1, mais par exemple avec des paramètres a, b, k, g appartenant aux complexes, k élevé à la puissance 3 et g(=1) étant là pour conserver un degré homogène 5 dans tous les éléments.
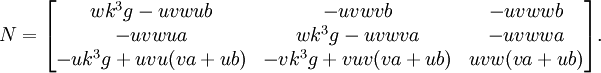
- Un point quelconque de la droite concernée est P = [ wX; wY; -(uX+vY) ] et on vérifie que N*P=w*k^3*g*P, tous les points de la droite sont donc fixes, N est l'identité sur la droite.
le Pp homogène et le plan classique de dim2
Qui plus est, si la droite de l'infini est la droite (0,0,1), alors on retrouve facilement les coordonnées cartésiennes du plan affine classique de dim2. Si l'on veut se ramener au plan "classique" de la géométrie euclidienne, des résultats spectaculaires sont obtenus, en particulier le calcul de l'angle de deux droites, le calcul de droites orthogonales, toutes le opérations sur l'angle droit; ce qui nous mènerait sans difficulté à trouver l'équation homogène d'un cercle de diamètre donné. Les coordonnées homogènes sont utilisées dans ces conditions par certains logiciels de programmation graphique 3D.
coordonnées orthonormées si l'infini est la droite (0,0,1) et si le corps K est celui des ComplexesFichier:.PNG
- La droite de l'infini est (0,0,1), les points de l'infini sont (a,b,0) a et b étant Complexes.
- Un point à l'infini (a,b,0) est aussi appelé la direction (a,b). Exemple, la direction (1,2) correspondant au point (1,2,0) voit passer les droites (2,-1,0) (2,-1,500) par exemple ainsi que (-6,3,9999) ou (i,-i/2,365), i étant un nombre complexe tel que i²=-1.
- Si l'on considère le plan projectif homogène privé des points à l'infini, alors les points sont de coordonnées homogènes (X,Y,Z) avec Z non-nul, et le point de dimension 2 (x,y)= (X/Z, Y/Z) est celui des coordonnées cartésiennes classiques. La droite non-infinie (A,B,C) est la droite cartésienne y=-A/B*x-C/B si B est non-nul, (A,0,C) est la droite cartésienne x=-C/A si B=0 et A non-nul, la droite (0,0,C) n'existant pas dans le plan affine.
- une des droites orthogonales à une droite donnée se calcule par une multiplication, par exemple:
, exemple dans lequel les coordonnées des droites sont exprimées sous forme homogène, la matrice de transformation aussi, dans cette matrice l'élément m3;3 est arbitraire ici on lui a donné la valeur 0,2 pourquoi pas?
- Deux points particuliers de ce plan projectif homogène se distinguent, il s'agit des "ombilics" ou "points cycliques", de représentants (1,i,0) (1,-i,0) que l'on peut appeler globalement ω1 et ω2 (omega1 et omega2). Lorsqu'on ne cherche pas à les individualiser, on parle de leur équation globale X²+Y²=0 ou de leur forme matricielle qui est (k étant un complexe non-nul) le "bipoint cyclique"= Bipcy=
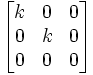 , équivalente à
, équivalente à 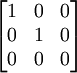 , ce qui signifie que c'est l'ensemble des points (X,Y,Z) tels que
, ce qui signifie que c'est l'ensemble des points (X,Y,Z) tels que - X²+Y²=
 . Contrairement aux apparences le forme matricielle est utile et très simple à manipuler.
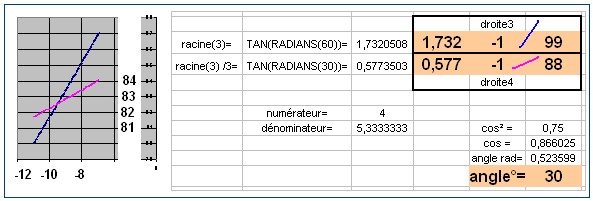
. Contrairement aux apparences le forme matricielle est utile et très simple à manipuler. - Un rapport anharmonique bien particulier peut être mis en évidence, il s'agit d'un nombre complexe-prolongé, mais on utilisera la tolérance de langage qui consiste à l'exprimer simplement en supposant que le deuxième membre n'est pas nul, ρ = exp(i * 2 * θ) = (cos(2 * θ) + isin(2 * θ)) , theta étant l'angle non-orienté de 2 droites non-infinies et non-complexes D1 et D2, et défini par rho = birapport(D1 et D2,ω1 et ω2), soit en termes mathématiques
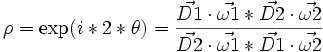 , exprimé ainsi ce n'est pas très opérationnel, mais après calculs, la partie réelle de ce nombre représentant le cos de l'angle double, on en déduit le cos² de l'angle simple par:
, exprimé ainsi ce n'est pas très opérationnel, mais après calculs, la partie réelle de ce nombre représentant le cos de l'angle double, on en déduit le cos² de l'angle simple par: 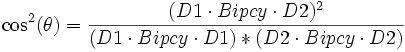 , soit si les deux droites s'expriment respectivement ainsi en coordonnées homogènes ou en coordonnées cartésiennes, D1=(A:B:F) ou y=mx+u, D2=(C:D:G) ou y=m'x+v
, soit si les deux droites s'expriment respectivement ainsi en coordonnées homogènes ou en coordonnées cartésiennes, D1=(A:B:F) ou y=mx+u, D2=(C:D:G) ou y=m'x+v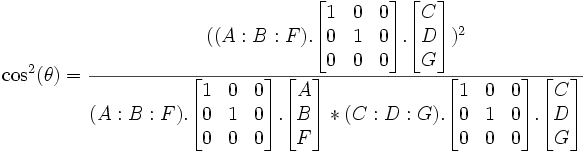
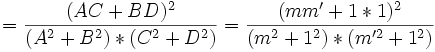 , cette formule donne 4 valeurs pour l'angle θ, le cosinus pouvant être positif ou négatif et l'angle étant positif ou négatif. Dans l'exemple des droites ci-dessus (1:2: 0,15) et (2:-1:0,75), l'application de la formule est simple car le numérateur est nul, d'où
, cette formule donne 4 valeurs pour l'angle θ, le cosinus pouvant être positif ou négatif et l'angle étant positif ou négatif. Dans l'exemple des droites ci-dessus (1:2: 0,15) et (2:-1:0,75), l'application de la formule est simple car le numérateur est nul, d'où ![\theta \equiv \frac{\pi}{2} [modulo \pi].](/pictures/frwiki/52/4bb6ea9af492538ca4d14694a2dd2ea6.png)
Dans le même ordre d'idées, le point à l'infini d'une droite non-infinie se calcule par la multiplication suivante
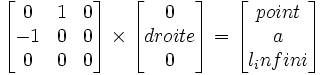 . exemple pour la droite1 ci-dessus,
. exemple pour la droite1 ci-dessus,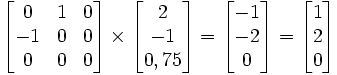 .
.- Un point à l'infini est encore plus simple, appelé "centre normal d'une droite"; c'est le point à l'infini de la direction orthogonale à cette droite, il est obtenu en multipliant la droite par le bipoint cyclique.
 . exemple pour la droite1 ci-dessus,
. exemple pour la droite1 ci-dessus,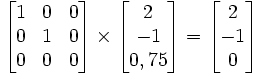 .
.
Un autre exemple de calcul d'angle:
- Comme on ne connaît que le carré du cosinus, les quatre angles non-orientés de ces deux droites sont
![\pm 30 [modulo 180].](/pictures/frwiki/101/ee0d6576851ecabcff9a7907a68f95a4.png)
Plus ou moins \pm [modulo \pi]</math> \vec{u} \cdot \vec{v} (,,) (,,) (,,) (,,) (,,) (,,) .- (,,) (,,) (,,) (,,) (,,) (,,) .
coniques dans le même cas particulier
coniques si l'infini est la droite (0,0,1) et si le corps K est celui des ComplexesNous n'envisagerons ici que les coniques ponctuelles (ensemble de points), les coniques tangentielles (ensemble de droites) ayant un traitement exactement dual. Une conique est un ensemple de points [X:Y:Z]définis par l'équation
 la matrice [a] étant symétrique. La conique dégènère en une bidroite si le détermnant en nul. Le bipoint cyclique n'est qu'un cas particulier de conique tangentielle dégénérée. La polaire d'un point [X:Y:Z] par rapport à la conique est la droite de coordonnées homogènes [U:V:W],
la matrice [a] étant symétrique. La conique dégènère en une bidroite si le détermnant en nul. Le bipoint cyclique n'est qu'un cas particulier de conique tangentielle dégénérée. La polaire d'un point [X:Y:Z] par rapport à la conique est la droite de coordonnées homogènes [U:V:W],
- [U:V:W]=
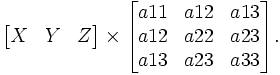
- [U:V:W]=
- Si le point [X:Y:Z] est sur la conique, alors la polaire ainsi définie est la tangente à la conique en ce point. Quelques exemples illustrent que l'on peut dessiner ainsi facilement des coniques réelles, polaires et tangentes en utilisant ces formules dans un tableur du commerce. Par exemple une ellipse, une hyperbole--
--
-- L'hyperbole a été dessinée sur un tableur avec une formule paramètrique qui donne ses trois coordonnées homogènes ainsi:
- X= (+1)*(t-u)*(v-t)
- Y= (+2)*(u-v)*(t-u)
- Z= (-1)*(v-t)*(u-v), tous ces nombres étant réels
- t, u, v étant trois nombres quelconques (3 paramètres pour parcourir la partie réelle d'une courbe est certes un peu luxueux, mais ça donne des formules très symétriques).
- La partie réelle de l'ellipse a été parcourue au myen d'un seul paramètre t
- X= 5t²+2t+1
- Y= -2(2t²-t-2)
- Z= 3(t²+1) .
- Applications numériques. Sur l'hyperbole comme sur l'ellipse ci-dessus, les points respectifs (1,2,1) et (1,0,1) ont pour polaire la droite de l'infini, ce sont donc les centres des coniques. Dans le premier cas si on calcule la bidroite tangente issue du centre on obtient une équation factorisable en deux droites, les asymptotes de l'hyperbole. Pour l'ellipse, on peut calculer la bidroite tangente issue d'un point extérieur (3,2,2)=(7.5 ,5,5), on obtient une équation factorisable en deux droites réelles que l'on peut ensuite traduire en coordonnées cartésiennes, y=-8x+13 et y= -4x/11+17/11; on vérifie que ces deux droites se coupent bien au point (3/2 , 1) et sont tangentes à l'ellipse. Dans le même ordre d'idées il existe des formules pour trouver les axes, les foyers, les diamètres conjugués, etc.
En dehors des PPH et de la démonstration du théorème fondamental -voir infra- on peut s'efforcer de raisonner sans aucune utilisation de coordonnées quelles qu'elles soient.
Axiomes de plans projectifs/barycentriques
Article détaillé : Axiomes de plans projectifs/barycentriques.Les plans projectifs barycentriques sont un peu moins généraux que les plans projectifs homogènes mais ont des propriétés très similaires. La notion de plan projectif barycentrique (PPB) est facile à imaginer intuitivement. Elle se définit à partir de la notion de barycentre dans un plan de la géométrie ordinaire auquel on rajoute des points, appelés de manière imagée et arbitraire points à l'infini.
Plans projectifs fondamental, de Pappus, de Désargues etc
Article détaillé : Axiomes de plans projectifs/Suite des axiomes.Transformations et configurations utiles
Article détaillé : Axiomes de plans projectifs/Suite des axiomes.Cascade de théorèmes entre ces axiomes
Article détaillé : Axiomes de plans projectifs/Suite des axiomes.des choix cornéliens pour approfondir les plans projectifs
Lorsque l’on aborde les plans projectifs selon une cascade d’axiomes reliés par une cascade de théorèmes il est possible d’hésiter, la tentation de tout démontrer d’un seul coup avec un théorème très puissant est forte, ou la tentation de tout démontrer algébriquement avec des formules de géométrie analytique.
Pour approfondir.
- Rappels : Axiomes de plans projectifs
- Axiomes de plans projectifs/Suite des axiomes
- Traité projectif des coniques
Articles de Géométrie projective ou voisins à consulter. [modifier] Hexagramme de Pascal • Axiomes de plans projectifs • Théorème de Pappus • Théorème de Desargues • Dualité • Axiomes de plans projectifs/Suite des axiomes • Axiomes de plans projectifs/homogènes • Axiomes de plans projectifs/barycentriques • Plan affine • Théorème d'Hessenberg • Traité projectif des coniques • Traité projectif des coniques/Dans un plan pappusien • Conique • Octonions • Relation d'équivalence • Structure de corps • Construction d'un cercle point par point • Construction d'une parabole tangente par tangente • Plan de Fano • Portail:Géométrie • Géométrie analytique • Géométrie synthétique • Géométrie • Géométrie projective • Géométrie non euclidienne • Division harmonique • Rapport anharmonique • Application projective • Fonction homographique • Perspective • Perspective conique • Infini • Droite (mathématiques) - Portail de la géométrie
Catégorie : Géométrie projective
Wikimedia Foundation. 2010.