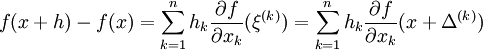- Théorème des accroissements finis généralisé
-
Théorème des accroissements finis
En analyse, le théorème des accroissements finis est un corollaire du théorème de Rolle. Pour toute fonction continue et dérivable d'une variable réelle, son accroissement entre deux valeurs est réalisable comme pente d'une de ses tangentes. Plus précisément :
Énoncé : Pour toute fonction à une variable réelle f : [a, b] →
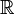 (a et b réels tels que a < b), supposée continue sur l'intervalle fermé [a, b] et dérivable sur l'intervalle ouvert ]a, b[, le théorème des accroissements finis annonce l'existence d'un réel c strictement compris entre a et b vérifiant :
(a et b réels tels que a < b), supposée continue sur l'intervalle fermé [a, b] et dérivable sur l'intervalle ouvert ]a, b[, le théorème des accroissements finis annonce l'existence d'un réel c strictement compris entre a et b vérifiant :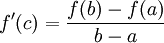 .
.En effet, sous ces hypothèses, la fonction
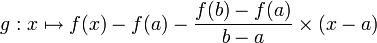 prend la même valeur en a et en b. En lui appliquant le théorème de Rolle, elle admet un point critique c strictement entre a et b. En ce point c, l'annulation de la dérivée implique l'égalité ci-dessus.
prend la même valeur en a et en b. En lui appliquant le théorème de Rolle, elle admet un point critique c strictement entre a et b. En ce point c, l'annulation de la dérivée implique l'égalité ci-dessus.Graphiquement, le théorème des accroissements finis indique que, pour toute sécante d'une courbe différentiable, il existe une tangente parallèle à la sécante.
Sommaire
Inégalité des accroissements finis
Soit f : [a, b] → R une fonction à valeurs réelles (a et b réels tels que a < b). Si :
- f est continue sur l'intervalle fermé [a, b]
- f est dérivable sur l'intervalle ouvert ]a, b[
- il existe k réel positif tel que, pour tout élément x de ]a, b[, |f'(x)| ≤ k,
alors
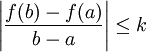
Démonstration :
On applique le théorème des accroissements finis et on majore |f'(c)| par k.
Pour donner une image, on peut illustrer ainsi le théorème : « Si la vitesse instantanée d'un véhicule ne peut pas dépasser 120 km/h, alors sa vitesse moyenne non plus. »
Théorème des accroissements finis généralisé
Ce théorème s'applique dans le cas de deux fonctions continues sur [a ; b] , dérivables sur ]a ; b[. Il stipule qu'il existe un réel c de l'intervalle ]a ; b[ tel que
Géométriquement, cette égalité signifie que toute courbe représentative d'une fonction de
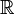 dans
dans 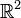 différentiable, possède une tangente parallèle à l'une quelconque de ses cordes. Dans le cas où g' ne s'annule pas sur ]a ; b[ , l'égalité peut s'écrire
différentiable, possède une tangente parallèle à l'une quelconque de ses cordes. Dans le cas où g' ne s'annule pas sur ]a ; b[ , l'égalité peut s'écrireSous cette forme, le théorème est utilisé pour démontrer la règle de L'Hôpital.
Démonstration :
- On applique le théorème de Rolle à la fonction
- La fonction h est bien continue sur [a ; b], dérivable sur ]a ; b[, et s'annule en a et b par conséquent h(a) = h(b). Donc il existe un réel c de ]a ; b[ tel que h'(c) = 0. Ce qui donne
- Si de plus g’ ne s'annule pas sur ]a ; b[, par contraposée du théorème de Rolle, on peut affirmer que
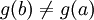 et il suffit de diviser par ces deux quantités pour obtenir
et il suffit de diviser par ces deux quantités pour obtenir
Théorème des accroissements finis et intégration
Le théorème des accroissements finis se reformule sous forme intégrale. Pour toutes fonctions d'une variable réelle u et v continues sur le segment [a, b], v ne s'annulant pas sur [a, b], il existe un réel c de ]a, b[ tel que
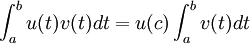 .
.L'écriture a un sens car les fonctions continues sont localement intégrables au sens de Riemann.
L'identité ci-dessus se prouve en appliquant le théorème des accroissements finis généralisé à des primitives F et V respectivement de uv et v. Comme la dérivée de V, à savoir v, ne s'annule pas par hypothèses, il existe en effet un réel c dans l'intervalle ]a, b[ vérifiant :
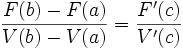 ,
,
Ce qui se réécrit plus simplement :
-
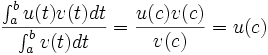 .
.
Exemple : pour une fonction v constante égale à 1, on retrouve ainsi le théorème de la moyenne : pour toute fonction continue à une variable réelle u sur le segment [a, b], il existe un réel c vérifiant :
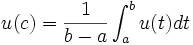 .
.
Dans
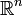
Soient
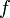 une fonction réelle dérivable sur un ouvert
une fonction réelle dérivable sur un ouvert 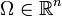 ,
, 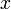 un point de
un point de 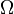 et
et 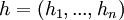 un point de
un point de 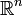 tel que
tel quealors il existe
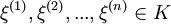 tels que
tels queavec
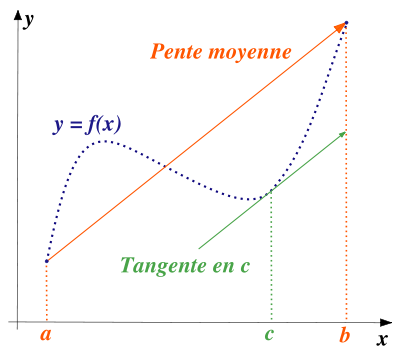
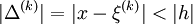 .
.Liens internes
- Portail des mathématiques
Catégories : Analyse réelle | Théorème de mathématiques
Wikimedia Foundation. 2010.

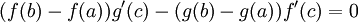
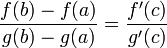
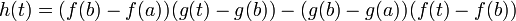
![\prod_{i=1}^n [x_i, x_i+h_i]=K\subset\Omega](/pictures/frwiki/55/79db4be6bdb4885d9a9793f9d2b05f2e.png)