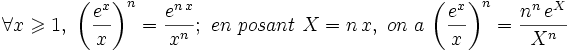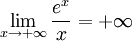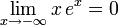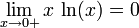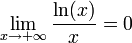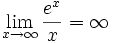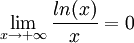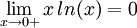Théorème des Croissances Comparées
- Théorème des Croissances Comparées
-
Théorème des Croissances Comparées
Le théorème des Croissances comparées est constitué de quelques résultats de limites de fonctions qui seraient qualifiées de 'formes indéterminées' par la méthode usuelle.
Énoncé des résultats
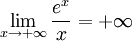
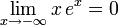
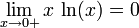
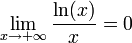
Démonstrations
On sait que (voir ci-après): 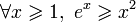
On a alors: 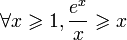
Par le théorème des gendarmes, on a le résultat voulu.
Preuve de 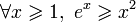 :
:
Soit ![\begin{align}f\ : & \ [1;+\infty]\to \mathbb{R} \\ \ & \qquad \quad x \mapsto e^x-x^2 \end{align}](/pictures/frwiki/56/8fcc703ea45277180f0cb23f8b62d260.png)
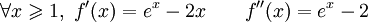
![\forall x\geqslant 1,\ e^x \geqslant 2 \quad \Rightarrow f''(x) \geqslant 0 \quad \Rightarrow f'\ est\ croissante\ sur\ [1;+\infty]](/pictures/frwiki/57/9ad883676076d2904b0237b4c4d36d7d.png)
![Or\ f'(1)=e-2\geqslant 0 \qquad \Rightarrow f\ est\ croissante\ sur\ [1;+\infty]](/pictures/frwiki/57/9ff52486af1fd91d01fbec6a128d1a1d.png)

D'où le résultat voulu.
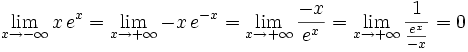
De la même manière, on utilise le résultat (montré par l'analyse de la fonction f(x)=ln(x)-sqrt(x) ): 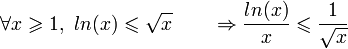
Par le théorème des gendarmes, on a le résultat voulu.
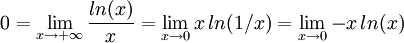
Résultats généralisés
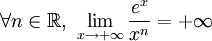
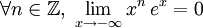
Démonstrations
Si n<0, le résultat est évident. Supposons 0<n<1 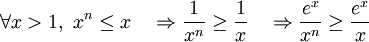 d'où le résultat par le théorème des gendarmes.
d'où le résultat par le théorème des gendarmes.
Si n>1, 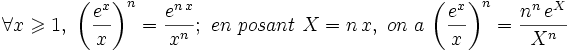
On peut alors appliquer le résultat de base.
Voir aussi
Limites de référence
Limite (mathématiques élémentaires)
Catégorie : Mathématiques élémentaires
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Théorème des Croissances Comparées de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Théorème des croissances comparées — Le théorème des croissances comparées est constitué de quelques résultats de limites de fonctions qui seraient qualifiées de formes indéterminées par la méthode usuelle. Sommaire 1 Énoncé des résultats classiques 1.1 Démonstrations 2 … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Croissance comparée — Théorème des Croissances Comparées Cet article fait partie de la série Mathématiques élémentaires Algèbre Logique Arithmétique Probabilités … Wikipédia en Français
Limites de référence — Cette page est une annexe de l article Limite (mathématiques élémentaires), conçue pour être une liste la plus complète possible des limites des suites usuelles, et des limites des fonctions usuelles partout où il y a lieu d étudier une limite, c … Wikipédia en Français
Limites De Référence — Cet article fait partie de la série Mathématiques élémentaires Algèbre Logique Arithmétique Probabilités … Wikipédia en Français
Limites de reference — Limites de référence Cet article fait partie de la série Mathématiques élémentaires Algèbre Logique Arithmétique Probabilités … Wikipédia en Français
TCC — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sigles d’une seule lettre Sigles de deux lettres > Sigles de trois lettres Sigles de quatre lettres … Wikipédia en Français
Tcc — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. {{{image}}} Sigles d une seule lettre Sigles de deux lettres > Sigles de trois lettres … Wikipédia en Français
Fonction puissance — En mathématiques, et plus spécialement en analyse, les fonctions puissances sont les fonctions définies par fa(x) = xa où a peut désigner un entier naturel, un entier relatif, ou même un réel que l on appelle l exposant de la fonction puissance.… … Wikipédia en Français
Opérations sur les limites — Cette page est une annexe de l article limite (mathématiques élémentaires), qui explique comment traduire en termes de limites les opérations usuelles : addition, multiplication, composition... Tous les résultats listés ici sont valables à… … Wikipédia en Français

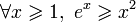
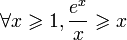
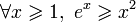 :
:![\begin{align}f\ : & \ [1;+\infty]\to \mathbb{R} \\ \ & \qquad \quad x \mapsto e^x-x^2 \end{align}](/pictures/frwiki/56/8fcc703ea45277180f0cb23f8b62d260.png)
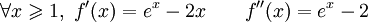
![\forall x\geqslant 1,\ e^x \geqslant 2 \quad \Rightarrow f''(x) \geqslant 0 \quad \Rightarrow f'\ est\ croissante\ sur\ [1;+\infty]](/pictures/frwiki/57/9ad883676076d2904b0237b4c4d36d7d.png)
![Or\ f'(1)=e-2\geqslant 0 \qquad \Rightarrow f\ est\ croissante\ sur\ [1;+\infty]](/pictures/frwiki/57/9ff52486af1fd91d01fbec6a128d1a1d.png)

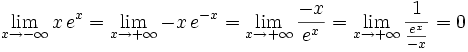
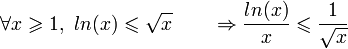
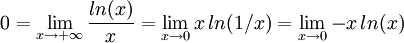
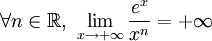
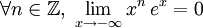
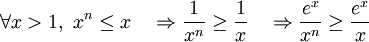 d'où le résultat par le théorème des gendarmes.
d'où le résultat par le théorème des gendarmes.