- Théorème de Miller
-
Effet Miller
On nomme Effet Miller l'influence du gain d'un amplificateur de tension inverseur sur ses propres caractéristiques d'entrée. (dans le cas d'un amplificateur non-inverseur, le même effet conduit à la génération d'impédances négatives)
Explication de l'Effet Miller
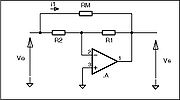
Le phénomène peut s'expliquer simplement grâce au schéma suivant :
On ne considère pour l'explication que les courants circulant dans la résistance de Miller Rm. Le montage est un amplificateur inverseur de gain Av = -R2/R1. Le courant circulant dans la résistance de Miller (Rm) est :
im = (Ve - (Ve x -R2/R1))/ Rm soit im = Ve x Av+1 /Rm .
La résistance équivalente vue de la source Ve est : Req = Ve / im = Rm / (Av+1)
La résistance Rm vue de la source Ve apparait donc comme ayant une valeur Av+1 fois plus faible.
La même démonstration est applicable à une capacité (condensateur) placée entre l'entrée et la sortie, avec pour effet de multiplier sa valeur par Av+1.
Cet effet explique entre autres l'augmentation de la capacité d'entrée d'un étage amplificateur inverseur due à la capacité base-collecteur (dans le cas d'un transistor bipolaire en émetteur commun), grille-drain (pour un transistor à effet de champ en source commune) ou grille-anode (pour un tube à vide en cathode commune).
Conséquences de l'effet Miller
L'Effet Miller a pour première conséquence une réduction des impédances d'entrée des montages électroniques. La seconde conséquence induite est une réduction de la bande passante des amplificateurs inverseurs (très sensible en haute fréquence) et la génération de déphasages nuisibles à la stabilité du montage.
Différentes techniques permettent de compenser, de réduire ou d'annuler l'effet Miller :
- le neutrodynage (compensation active);
- le montage amplificateur base commune (ou grille commune) (pas d'effet Miller);
- le montage cascode (étage d'entrée de gain en tension unitaire + étage en base commune).
Applications
L'effet Miller trouve cependant des applications (parfois insoupçonnées bien que directement induites) notamment dans la réalisation de filtres actifs en permettant la réalisation de capacités variables de plusieurs micro-farads ou d'inductances ultra-légères de plusieurs Henrys!
C'est également l'effet Miller qui a permis de fixer de manière fiable le produit Gain.bande des amplificateurs opérationnels depuis l'avènement du µA741 !
- Portail de l’électricité et de l’électronique
Catégorie : Amplificateur électronique
Wikimedia Foundation. 2010.