Theorie des codes

Théorie des codes

En théorie de l'information, la théorie des codes traite des codes et donc de leurs propriétés et leurs aptitudes à servir sur différents canaux de communication. On distingue deux modèles de communication : avec et sans bruit. Sans bruit, le codage de source suffit à la communication. Avec bruit, la communication est possible avec les codes correcteurs.

Histoire

En définissant l'information de façon mathématique, l'étape-clé à la fondation de la théorie des codes a été franchie par Claude Shannon. D'autres définitions existent, mais l'entropie de Shannon a été la plus prolifique. Ainsi, on est apte à répondre aux deux questions fondamentales de la théorie de l'information : quelles sont les ressources nécessaire à la transmission de l'information et la quantité d'information que l'on peut transmettre de façon fiable.

C'est de cette dernière question du codage de canal dont traite la théorie des codes. En répondant aux deux questions de base de la théorie de l'information, Shannon n'a justement pas fourni un ensemble très puissant de codes correcteurs. En particulier, il n'a pas déterminé d'exemple de code qui atteint la limite prévue par son théorème du codage de canal.

C'est ce vide que comble la théorie des codes. Il existe de nos jours une multitude de méthodes visant à produire de bons codes correcteurs.

Propriétés des codes

On distingue d'abord les codes par la quantité d'information transmise par un symbole. Le canal binaire symétrique étant le plus commun, on considérera souvent un code binaire. Il existe cependant aussi des codes trinaires et, en général, des codes q-aires.

Les noms de variables suivants sont la plupart du temps, utilisés par convention. C est un code contenant M mots de code, c'est-à-dire, de dimension M. La longueur d'un mot de code est dénotée par n. Un tel code est dit code (n,M).

Détection et correction d'erreurs

La plupart des codes s'utilisent soit pour la détection ou la correction d'erreur.

Distance minimale et décodage

Article détaillé : Méthodes de décodage.

La distance minimale d'un code influe la probabilité d'erreur de décodage. La distance minimale est un paramètre important, dénoté d. Un tel code est dit code (n,M,d).

Familles de codes

Codes équivalents

Deux codes sont équivalents si toutes leurs propriétés de correction d'erreur sont les mêmes.

Types de codes

On distingue généralement trois types de codes.

• Un code linéaire est un code correcteur à qui l'on impose une structure d'espace vectoriel.

• Un code cyclique est un code correcteur qui a davantage de structure que celle d'un espace vectoriel. En général, on peut concevoir les mots de code comme des polynômes. Exemples : le code de Reed-Solomon et le code de Hamming.

• Un code non linéaire est un code correcteur qui peut être construit d'une variété de façons, sans obtenir la structure d'un espace vectoriel.

Il y a un petit nombre de cas spéciaux. Un code trivial est un code qui recopie littéralement le message initial, d'où sa trivialité. Un code systématique est un code pour lequel le message a encodé est inclus dans la message encodé.

Par ailleurs, certains codes correcteurs peuvent être utilisés comme codes quantiques.

D'autres types de codes importants sont :

• code algébrique

• code aléatoire

Familles

Les codes correcteurs peuvent aussi être classés par familles.

• Un code de parité ajoute un ou plusieurs bits de parité au message.

• Un code de répétition envoie plusieurs copies de chaque bit à être transmis.

• Les codes de Hamming forment la famille la plus connue. Les codes de Hamming binaires sont équivalents aux codes cycliques et certains non binaires le sont aussi.

• Un code de Golay est un code linéaire considéré important en théorie et en pratique.

• Un code de Reed-Müller est un code linéaire dont les propriétés de décodage sont considérées particulièrement pratiques.

• Les codes BCH sont une généralisation des codes de Hamming. Ils s'agit aussi de codes cycliques. Un cas particulier est le code de Reed-Solomon.

• Un code de résidu quadratique est un code cyclique basé sur la résiduosité quadratique.

• Un code de Goppa qui, comme les codes cycliques, est basé sur un polynôme, dit polynôme de Goppa.

• Un code stabilisateur est basé sur la mesure d'un syndrome, c'est-à-dire d'un vecteur dans $F_2^{n-k}$.

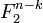• Un code expandeur est un code linéaire avec lequel il est toujours possible de corriger une fraction constante d'erreurs.

• Les codes superconcentrateur de Spielman sont les seuls codes pouvant être codés et décodés en temps linéaire.

• Un code alternant est un code linéaire d'importance pratique.

• Un code de Hadamard est un code généré à partir d'une matrice de Hadamard.

• Un code LDPC est un code qui possède une matrice de parité creuse.

Combinaisons de codes

On peut obtenir de nouveaux codes à partir d'opérations qui combinent un ou deux codes de base.

• opérations triviales : poinçonnage ou raccourcissement
• concaténation : code de Forney, code de Justesen
• produit

Autres propriétés

On distingue aussi certaines classes de codes par leurs propriétés.

• code intersectant
• code séparant
• code MDS

Code et « design »

Il y a une connexion entre les codes et les designs combinatoriaux.

Le problème principal de la théorie des codes

Soit A_q(n,d) le plus grand M pour lequel il existe un code (n,M,d) et q-naire. Le problème principal de la théorie des codes est de déterminer ces valeurs.

Codage de source

Article détaillé : Codage de source.

Le but du codage de source peut être de compresser l'information répétitive du langage, sa redondance. Pour toute langue, on peut considérer l'entropie d'un message, c'est-à-dire la quantité d'information transmise. Ceci donne lieu au théorème du codage de source.

Codage de canal

Le but est d'ajouter de l'information redondante à un message pour compenser le bruit sur le canal de communication. Ceci donne lieu au théorème du codage de canal et c'est à celui-ci qu'on doit l'origine de la théorie des codes.

Certains problèmes cryptographiques sont basés sur l'hypothèse de la difficulté du décodage.

Théorie algébrique des codes

Article détaillé : Théorie algébrique des codes.

La théorie algébrique des codes est un sous-domaine de la théorie des codes où les propriétés des codes sont exprimées algébriquement. Autrement dit, l'approche est algébrique par opposition à l'approche traditionnelle qui est probabiliste. ^[1] On y étudie principalement :

• la construction de « bons » codes, c'est-à-dire avec certains paramètres souhaitables, tels :
  • la longueur des mots de code
  • le nombre total de mots de code valides
  • la distance de Hamming minimale entre deux mots de code valides
• le décodage efficace de ces codes

Références

1. ↑ Préface de : Elwyn R. Berlekamp, Algebraic Coding Theory, McGraw-Hill, 1968, 466 p.

Voir aussi

Bibliographie

• Jean-Guillaume Dumas, Jean-Louis Roch, Eric Tannier, Sebastien Varrette "Théorie des codes (Compression, cryptage, correction)", ISBN 978-2-10-050692-7 Site de l'ouvrage
• Bruno Martin "Codage, cryptologie et applications", ISBN 978-2-88074-569-1 Site de l'ouvrage

Liens externes

• (fr) Notions de communication numérique du département SI de la Polytechnique Nice-Sophia
• (fr) Polycopié du cours dispensé à l'Ensimag

Ce document provient de « Th%C3%A9orie des codes ».