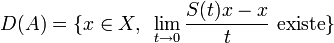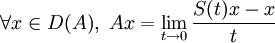- Theoreme de Hille-Yosida
-
Théorème de Hille-Yosida
En théorie des semi-groupes, le théorème de Hille-Yosida est un outil puissant et fondamental reliant les propriétés de dissipation de l'énergie d'un opérateur non borné
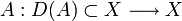 à l'existence-unicité et la régularité des solutions d'une équation différentielle (E)
à l'existence-unicité et la régularité des solutions d'une équation différentielle (E) 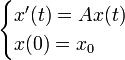 .
.Sommaire
Semi-groupes
La théorie des semi-groupes doit son origine à l'étude du flot d'une équation différentielle ordinaire autonome en dimension finie ainsi que de l'exponentielle d'opérateurs.
Définitions
- Soit X un espace de Banach; on dit que la famille d'opérateurs linéaires
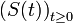 est un semi-groupe (fortement continu) si :
est un semi-groupe (fortement continu) si :
- (i)
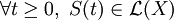
- (ii)
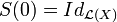
- (iii)
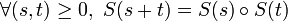
- (iv)
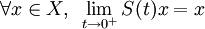
La condition (iv) est équivalente à ce que
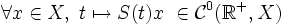 . Si on remplace (iv) par (iv) * :
. Si on remplace (iv) par (iv) * : 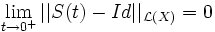 on dit que
on dit que 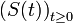 est uniformément continu.
est uniformément continu.On retrouve (vaguement) avec cette définition la notion de famille à un paramètre de difféomorphismes bien connue en théorie des EDO.
- On définit le générateur infinitésimal (A,D(A)) d'un un semi-groupe fortement continu
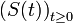 comme l'opérateur non borné
comme l'opérateur non borné 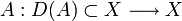 où:
où:
Dans le cas où D(A) = X et
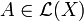 la famille d'opérateurs
la famille d'opérateurs 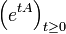 (définie classiquement par sa série) est un semi-groupe fortement continu de générateur infinitésimal A: c'est pourquoi on note parfois abusivement S(t) = etA.
(définie classiquement par sa série) est un semi-groupe fortement continu de générateur infinitésimal A: c'est pourquoi on note parfois abusivement S(t) = etA.- On dit que le semi-groupe
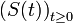 est de contraction si
est de contraction si 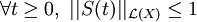 .
.
Propriétés des semi-groupes de contraction
- Théorème 1: soit X un espace de Banach,
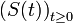 un semi-groupe de contraction sur X et (A,D(A)) son générateur infinitésimal. Alors:
un semi-groupe de contraction sur X et (A,D(A)) son générateur infinitésimal. Alors:
- (i)
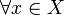 le flot
le flot 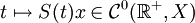
- (ii)
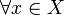 et
et 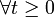
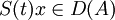 , le flot
, le flot 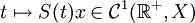 et vérifie x'(t) = Ax(t)
et vérifie x'(t) = Ax(t) - (iii) (A,D(A)) est fermé de domaine dense.
- Théorème 2 (caractérisation des générateurs infinitésimaux): soit
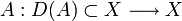 un opérateur non borné sur X. On a l'équivalence:
un opérateur non borné sur X. On a l'équivalence:
- (i) (A,D(A)) est le générateur infinitésimal d'un semi-groupe de contraction
- (ii) D(A) est dense et pour toute condition initiale
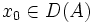 il existe une unique solution
il existe une unique solution 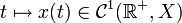 de (E).
de (E).
De plus sous cette hypothèse la solution x(t) est à valeurs dans D(A) et vérifie
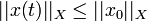 ainsi que
ainsi que 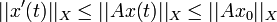 (inégalités d'énergie).
(inégalités d'énergie).On commence à voir apparaître le lien entre le problème (E) et la notion de semi-groupe. Pour préciser, il faut maintenant introduire la notion d'opérateur dissipatif.
Opérateurs dissipatifs
Définitions
- Un opérateur (A,D(A)) est dissipatif si
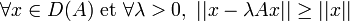 . Dans le cas où X = H est hilbertien on montre que A est dissipatif si et seulement si
. Dans le cas où X = H est hilbertien on montre que A est dissipatif si et seulement si 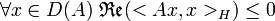 .
.
Remarque: Si (A,D(A)) est un opérateur dissipatif alors
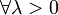 l'opérateur (Id − λA) est injectif car
l'opérateur (Id − λA) est injectif car 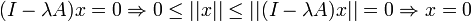 .
.- Si de plus
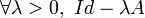 est surjectif on dit que (A,D(A)) est maximal-dissipatif (ou m-dissipatif). On peut montrer que
est surjectif on dit que (A,D(A)) est maximal-dissipatif (ou m-dissipatif). On peut montrer que 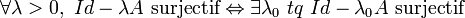 . En pratique pour montrer qu'un opérateur est m-dissipatif on montre d'abord à la main qu'il est dissipatif et on résout ensuite un problème variationnel pour une valeur λ0 bien choisie (par exemple avec le théorème de Lax-Milgram, voir exemple de l'équation de la chaleur traité plus bas).
. En pratique pour montrer qu'un opérateur est m-dissipatif on montre d'abord à la main qu'il est dissipatif et on résout ensuite un problème variationnel pour une valeur λ0 bien choisie (par exemple avec le théorème de Lax-Milgram, voir exemple de l'équation de la chaleur traité plus bas).
Dans ce cas l'opérateur (Id − λA) est un isomorphisme (a priori non continu) de L(A,X) et on note Jλ = (Id − λA) − 1. De plus, comme
![||J_{\lambda}y||_X \leq ||(Id-\lambda A)[J_{\lambda}y]||_X \leq ||y||_X](/pictures/frwiki/102/fbad7312b4d7fa3feffc0caca79a9a50.png) ,
, 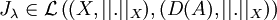 . Nous allons voir que cette propriété de continuité peut être améliorée (on va rendre moins fine la topologie sur (D(A), | | . | | X) en munissant D(A) d'une norme | | . | | D(A)).
. Nous allons voir que cette propriété de continuité peut être améliorée (on va rendre moins fine la topologie sur (D(A), | | . | | X) en munissant D(A) d'une norme | | . | | D(A)).Propriétés des opérateurs m-dissipatifs
Prop 1: si (A,D(A)) est m-dissipatif alors c'est un opérateur fermé.
Corollaire 1: pour
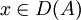 on pose | | x | | D(A) = | | x | | X + | | Ax | | X. Alors | | . | | D(A) est une norme pour laquelle D(A) est un espace de Banach et
on pose | | x | | D(A) = | | x | | X + | | Ax | | X. Alors | | . | | D(A) est une norme pour laquelle D(A) est un espace de Banach et 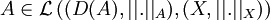 .
.Prop 2: si H est un espace Hilbertien et
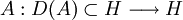 est m-dissipatif alors il est à domaine dense.
est m-dissipatif alors il est à domaine dense.Prop 3: réciproquement si
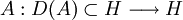 est de domaine dense, dissipatif, fermé et tel que son adjoint (A * ,D(A * )) est dissipatif alors (A,D(A)) est m-dissipatif.
est de domaine dense, dissipatif, fermé et tel que son adjoint (A * ,D(A * )) est dissipatif alors (A,D(A)) est m-dissipatif.Corollaire 3: toujours dans le cadre hilbertien
- (i) si (A,D(A)) est dissipatif autoadjoint à domaine dense alors il est m-dissipatif
- (ii) si (A,D(A)) est antioadjoint à domaine dense alors il est m-dissipatif
Remarque: dans (ii) la condition de dissipativité n'est pas nécessaire car (A,D(A)) autoadjoint entraîne que < Ax,x > H = 0 donc la dissipativité, voir l'exemple de l'équation des ondes plus bas.
Théorème de Hille-Yosida
Enoncé
- Théorème 3 (Hille-Yosida): soit X un espace de Banach et
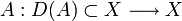 un opérateur non borné. On a l'équivalence
un opérateur non borné. On a l'équivalence
- (i) (A,D(A)) est m-dissipatif à domaine dense
- (ii) (A,D(A)) est le générateur infinitésimal d'un semi-groupe de contraction
Le point (i) du théorème précédent peut être réécrit en termes de résolvante : (i') (A,D(A)), opérateur fermé à domaine dense, vérifie
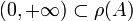 et
et 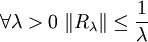 .
.Ainsi sous ces hypothèses et d'après le théorème 2 pour toute condition initiale
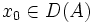 il existe une unique solution forte
il existe une unique solution forte 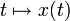 dans
dans 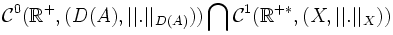 . Lorsque la condition initiale est prise quelconque dans X on a une solution faible
. Lorsque la condition initiale est prise quelconque dans X on a une solution faible 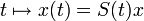 de classe seulement
de classe seulement 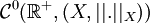 ( et on montre que toute solution faible est limite dans X de solutions fortes).
( et on montre que toute solution faible est limite dans X de solutions fortes).Régularité des solutions
On constate que la régularité de la solution est étroitement liée au choix de la condition initiale en fonction du domaine de A: il est donc naturel de penser qu'en imposant plus de "régularité" à x0 on obtienne plus de régularité sur les solutions. Plus précisément on pose pour
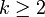
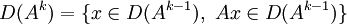 . Alors on a le
. Alors on a leThéorème 4: on peut munir les D(Ak) des normes
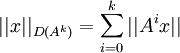 pour lesquels ce sont des espaces de Banach. De plus si la condition initiale
pour lesquels ce sont des espaces de Banach. De plus si la condition initiale 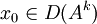 alors la solution est de classe
alors la solution est de classe 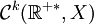 et
et 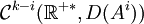 pour i = 1...k et au sens des topologies précédentes.
pour i = 1...k et au sens des topologies précédentes.Exemples
L'équation de la chaleur
On se donne Ω un ouvert borné de classe
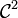 de
de 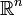 et on cherche à résoudre l'équation de la chaleur
et on cherche à résoudre l'équation de la chaleur 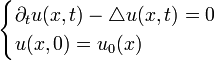 sur
sur ![(x,t)\in \Omega \times [0,+\infty]](/pictures/frwiki/49/19877724639c34842b23ba17f4e7ed6f.png) pour une condition initiale donnée. On peut réécrire cette EDP sous la forme d'une EDO y'(t) = Ay(t) en posant X = H = L2(Ω),
pour une condition initiale donnée. On peut réécrire cette EDP sous la forme d'une EDO y'(t) = Ay(t) en posant X = H = L2(Ω), 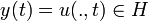 et en définissant (A,D(A)) par
et en définissant (A,D(A)) par 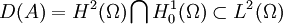 et
et 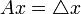 pour tout
pour tout 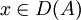 . Nous sommes dans le bon cadre pour utiliser la théorie des semi-groupes et le théorème de Hille-Yosida; reste à montrer que l'opérateur A est m-dissipatif. Il est bien connu que le laplacien est un opérateur autoadjoint (on a
. Nous sommes dans le bon cadre pour utiliser la théorie des semi-groupes et le théorème de Hille-Yosida; reste à montrer que l'opérateur A est m-dissipatif. Il est bien connu que le laplacien est un opérateur autoadjoint (on a 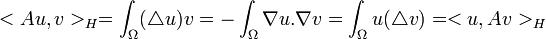 par double intégration par parties) et que D(A) est dense dans L2(Ω), il suffit donc de montrer qu'il est dissipatif ou de façon équivalente que
par double intégration par parties) et que D(A) est dense dans L2(Ω), il suffit donc de montrer qu'il est dissipatif ou de façon équivalente que 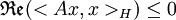 . Or tout
. Or tout 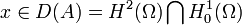 est de trace nulle, donc en intégrant par parties
est de trace nulle, donc en intégrant par parties 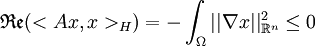 . Le corollaire 3 et le théorème de Hille-Yosida permettent enfin de conclure quant à l'existence-unicité et la régularité des solutions. Remarquer que
. Le corollaire 3 et le théorème de Hille-Yosida permettent enfin de conclure quant à l'existence-unicité et la régularité des solutions. Remarquer que 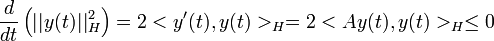 : on retrouve bien sur le côté dissipatif et irréversible de l'équation de la chaleur.
: on retrouve bien sur le côté dissipatif et irréversible de l'équation de la chaleur.L'équation des ondes
L'équation des ondes homogène se formule dans un domaine Ω suffisamment régulier (c'est-à-dire
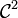 en pratique) et sur un intervalle de temps [0,T) (avec T > 0) selon
en pratique) et sur un intervalle de temps [0,T) (avec T > 0) selon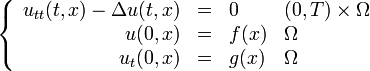
On se place dans la théorie des semi-groupes en mettant l'équation précédente au premier ordre en temps. On pose alors
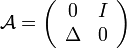 ,
, 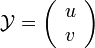 (avec v = u' ) et
(avec v = u' ) et 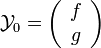 l'équation devient alors
l'équation devient alors 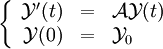 .
.Le domaine du Laplacien étant
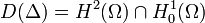 , celui de
, celui de 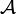 est
est 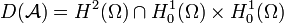 sur
sur 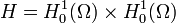 . Les conditions initiales seront alors prises dans H.
. Les conditions initiales seront alors prises dans H.
Reste à vérifier que nous sommes bien dans les conditions d'application du théorème de Hille-Yosida :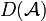 est dense dans H.
est dense dans H.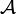 est fermé.
est fermé.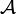 est dissipatif. Ce point mérite une preuve : on utilise la caractérisation (i') du théorème. Soient λ > 0 et
est dissipatif. Ce point mérite une preuve : on utilise la caractérisation (i') du théorème. Soient λ > 0 et 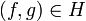 . L'équation résolvante s'écrit en (u,v)
. L'équation résolvante s'écrit en (u,v)
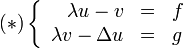 d'où (λ2I − Δ)u = λf + g qui admet une unique solution dans
d'où (λ2I − Δ)u = λf + g qui admet une unique solution dans 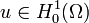 via Lax-Milgram (car d'une part λ2 > 0 et d'autre part les valeurs propres du Laplacien sont strictement négatives donc (λ2I − Δ) est un opérateur elliptique dont la forme bilinéaire associée vérifie les hypothèses du théorème de Lax-Milgram). Et alors v = λu − f est dans
via Lax-Milgram (car d'une part λ2 > 0 et d'autre part les valeurs propres du Laplacien sont strictement négatives donc (λ2I − Δ) est un opérateur elliptique dont la forme bilinéaire associée vérifie les hypothèses du théorème de Lax-Milgram). Et alors v = λu − f est dans 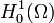 .
.L'estimation de l'opérateur résolvant Rλ vient du produit scalaire de ( * )2 par v en remplaçant u par sa valeur dans ( * )1:
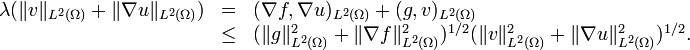
D'où, puisque (u,v) = Rλ(f,g), on obtient l'estimation attendue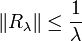 . Le semi-groupe engendré par
. Le semi-groupe engendré par 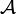 est donc un semi-groupe de contraction.
est donc un semi-groupe de contraction.- Portail des mathématiques
Catégorie : Théorème de mathématiques - Soit X un espace de Banach; on dit que la famille d'opérateurs linéaires
Wikimedia Foundation. 2010.