Theoreme d'Artin-Wedderburn

Théorème d'Artin-Wedderburn

En mathématiques et plus particulièrement en algèbre le Théorème d'Artin-Wedderburn traite de la structure d'algèbre ou d'anneau semi-simple.

Il correspond au théorème fondamental des structures semi-simples et permet d'expliciter exactement leur nature. Elles correspondent à des produits d'algèbres des endomorphismes de modules sur des corps non nécessairement commutatifs.

Il est démontré une première fois dans le cadre des algèbre sur un corps commutatif par Joseph Wedderburn en 1907 puis généralisé par Emil Artin sur les anneaux pour trouver sa forme définitive en 1927.

Ce théorème est au cœur de plusieurs théories, on peut citer les représentations d'un groupe fini ou non, la théorie des anneaux où il permet par exemple de construire des corps non commutatifs et encore celle des structures semi-simples en général.

Enoncés

Ce théorème a connu plusieurs versions au cours de son histoire, voici les trois principales :

La première version correspond au théorème de Burnside, elle ne traite que du cas d'une algèbre simple :

• Si E est un espace vectoriel de dimension finie, alors l'algèbre L_K(E) est simple.

Ce deuxième théorème correspond, en termes actuels au théorème de Wedderburn, il traite des algèbres sur un corps commutatif :

• Une algèbre semi-simple sur un corps commutatif K est isomorphe à un produit d'algèbres d'endomorphismes sur des sur-corps de K.

La troisième version s'exprime en termes d'anneau, elle porte maintenant le nom de théorème d'Artin-Wedderburn :

• Un anneau semi-simple tel que tout idéal simple est de dimension finie sur son corps d'endomorphismes, est isomorphe à un produit d'algèbres d'endomorphismes de modules sur des corps a priori distincts et gauches.

Les corps dont il est question ici sont a priori des corps gauches, c'est-à-dire non commutatifs.

L'article sur les algèbres semi-simples montre que la version d'Artin se généralise immédiatement aux algèbres.

Démonstrations

Définitions

Tout au long de ce paragraphe, les notations suivantes sont utilisées : K désigne corps commutatif, L une algèbre sur K et E un espace vectoriel sur K. Plusieurs définitions sont utilisées pour exprimer le théorème.

L'algèbre L est aussi un module sur l'anneau L. Ses sous-modules sur L ne disposent plus de la notion de dimension, car la structure d'espace vectoriel est absente sous cet angle. Elle est remplacée par la définition suivante :

• La longueur d'un module L, est la borne supérieure de l'ensemble des entiers n telle qu'il existe une suite strictement croissante au sens de l'inclusion de sous A-modules de L.

On suppose ici que L en tant que L module est semi-simple, ce qui correspond à la définition suivante :

• Soit S un sous-module de L, F est dit facteur direct si et seulement si F admet un sous-module supplémentaire.

Comme L opère à droite et à gauche sur le module, un sous-module est un idéal bilatère.

• Un module L est dit semi-simple si et seulement si tout sous-module est facteur direct.

Une telle algèbre est dite semi-simple. Sa structure, en tant que module est connue :

• Si le module L semi-simple, alors il est somme directe de ses composantes isotypiques.

$\mathbb L \simeq \bigoplus_{i} S_i^{\alpha_i}$

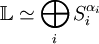
Ici, (S_i) désigne une famille maximale au sens de l'inclustion de sous-modules non isomorphes deux à deux et α_i le nombre de copies de S_i dans sa composante isotypique. Avec les définitions suivantes :

• Un sous-module S du module L est dit simple si et seulement s'il ne contient pas d'autres sous-modules que lui-même et l'ensemble nul.
• La composante isotypique du sous-module S dans L est le sous-module engendré par tous les sous-modules de L isomorphe à S.

Dans tout le paragraphe concernant les démonstrations, les composantes isotypiques sont notés S_i, leur nombre n, leur degré de multiplicité α_i, et D_i désigne l'opposé du corps des endomorphismes de S_i en tant que L module. On rappelle la définition suivante :

• L'anneau opposé de A est l'anneau noté ici A^op muni de la multiplication définie par :

$\forall a,b \in \mathbb A \quad a^{op}.b^{op}=ba\;$

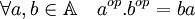
Démonstration de Burnside

• Si E est un espace vectoriel de dimension finie, alors l'algèbre L_K(E) est simple.

Soit f un endomorphisme non nul, montrons que le plus petit idéal bilataire contenant f est l'algèbre entière. Il existe un élément e₁ de E à l'extérieur du noyau de f, car sinon f serait nul ce qui n'est pas le cas. Notons a l'image de e₁ par f. Le théorème de la base incomplète montre qu'il existe une famille (e_i) tel que l'ensemble des indices contient 1 et qui est une base de E. Soit h₁ l'application linéaire qui associe le vecteur nul à tous les vecteurs de la base sauf à e₁ qui a pour image lui-même. Soit h₂ une application ayant pour image de a e₁. Alors la composition g = h₂ o f o h₁ a est un projecteur sur e₁ parallèlement à l'espace vectoriel engendré par les autres vecteurs de la base, de plus g est un élément de l'idéal contenant f. Soit p_i l'application linéaire nulle sur la base sauf sur e_i qui à pour image e₁. Soit q_j une application linéaire tel que l'image de e₁ est égale à e_j. Alors q_j o g p_i est une famille de l'idéal engendré par f. Cette famille est génératrice de L(E), ce qui termine la démonstration.

Cette démonstration s'applique aussi dans le cas des modules sur un corps gauche. Ce cas est important car, dans le cas des algèbres semi-simples, il établit la réciproque du théorème d'Artin-Wedderburn.

Démonstration d'Artin

Le théorème de Wedderburn est clairement un cas particulier de celui d'Artin. La démonstration d'Artin étant relativement simple, uniquement celle-ci est donnée dans cet article.

• Si L est semi-simple et si toute composante isotypique est de dimension finie sur son corps d'endomorphismes, alors la composante isotypique de S_i est isomorphe à l'ensemble des endomorphismes d'un module de dimension α_i sur le corps D_i, et L est isomorphe à la somme directe de ces algèbre d'endomorphismes.

$si\quad \mathbb L \simeq \bigoplus_i S_i^{\alpha_i}\quad alors \quad \mathbb L \simeq \bigoplus_i \mathcal L_{\mathbb D_i}(\mathbb D_i^{\alpha_i})\quad avec \quad \mathbb D_i = \mathcal L_{\mathbb L} (S_i)^{op}$

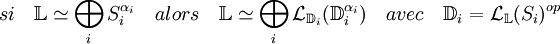
Remarque : parler de dimension d'un module fait ici sens car le module possède pour anneau un corps. Cette structure n'est néanmoins pas celle d'un espace vectoriel, car le corps est a priori gauche.

Démontrons tout d'abord le lemme suivant :

• L'ensemble des endomorphismes de L est isomorphe à la somme directe des ensembles des endomorphismes des composantes isotypiques.

$\mathcal L_{\mathbb L}(\mathbb L) \simeq \mathcal L_{\mathbb L}(S_i^{\alpha_i})$

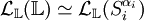
Il est clair que la somme directe est incluse dans l'ensemble des endomorphismes de L.

Réciproquement, le paragraphe Décomposition canonique de l'article Module semi-simple montre que tout sous-module simple de la composante isotypique de S_i est isomorphe à S_i. Le lemme de Schur assure qu'il n'existe pas de morphisme autre que le morphisme nul entre deux modules simple non isomorphes. En conséquence le seul morphisme entre la composante isotypique de S_i et S_j si i et j sont différents sont les morphismes nuls, ce qui termine la démonstration de ce lemme.

Démontrons ensuite le lemme suivant :

• L'opposé de l'anneau des endomorphismes de la composante isotypique de S_i est isomorphe à l'ensemble des endomorphismes d'un espace vectoriel de dimension α_i sur le corps D_i^op.

$\mathcal L_{\mathbb L}(S_i^{\alpha_i})^{op} \simeq \bigoplus_{j=1}^{\alpha_i}\mathcal L_{\mathbb D}(\mathbb D^{\alpha_i})$

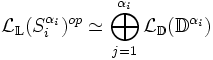
Le raisonnement est analogue à celui du lemme précédent. Si S_ij pour j variant de 1 à α_i désigne une décomposition en somme directe de la composante isotypique de S_i, alors chaque facteur S_ij est isomorphe à S_i. L'ensemble des endormorphismes de la composante isoptypique est donc isomorphe à l'ensemble des matrices à coefficients dans l'ensemble des endomorphismes du module S_i. L'ensemble des coefficients est un corps (non nécessairement commutatif) dont l'opposé est D_i (cf Décomposition canonique de l'article Module semi-simple). L'isomorphisme canonique entre l'ensemble des matrices carrées de dimension α_i et l'ensemble des endomorphismes sur un espace vectoriel de dimension α_i termine la démonstration du deuxième lemme.

Pour conclure, il suffit alors de remarquer que l'opposé de L est isomorphe à l'ensemble des endomorphismes de L.

Notes et références

Liens externes

• (fr) Théorie des algèbres simples J.P. Serre Séminaire Henri Cartan
• (fr) Algèbre commutative A. Chambert-Loir
• (en) Finite group representation for the pure mathematician Peter Webb
• (fr) Théorie des algèbres semi-simples P. Cartier Séminaire Sophus Lie
• (fr) Quelques applications des algèbres de matrices à la théorie des corps non commutatifs Erwan Biland
• (en) Références historiques Par le site de l'université de St Andew

Références

• Serge Lang, Algèbre, Dunod, 2004, 926 p. (ISBN 2100079808) [détail des éditions]
• N. Bourbaki, Algèbre commutative Chapitre VIII et IX Masson 1983
• Artin Nesbitt Thrall Rings with minimum condition. Ann Arbor, Univ. of Michigan Press, 1948
• S. Lang and J. T. Tate E. Artin The collected papers of Emil Artin Reading, Mass.-London 1965
• P. Webb S. Priddy J. Carlson Group Representations, Cohomology, Group Actions, and Topology University of Wisconsin, Madison 1998

Ce document provient de « Th%C3%A9or%C3%A8me d%27Artin-Wedderburn ».