Test de kolmogorov-smirnov

Test de Kolmogorov-Smirnov

En statistiques, le test de Kolmogorov-Smirnov est un test d'hypothèse utilisé pour déterminer si un échantillon suit bien une loi donnée connue par sa fonction de répartition continue, ou bien si deux échantillons suivent la même loi.

Principe

Ce test repose sur les propriétés des fonctions de répartition empirique (en) : si 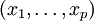$(x_1,\dots,x_p)$ est un échantillon de n variables aléatoires indépendantes à valeurs réelles, alors la fonction de répartition empirique de cet échantillon est définie par 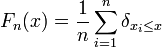$F_n(x)={1 \over n}\sum_{i=1}^n \delta_{x_i\leq x}$ avec $\delta_{x_i\leq x} = \left\{\begin{matrix}1 & \mathrm{si}\ x_i\leq x, \\ 0 & \mathrm{sinon}.\end{matrix}\right.$

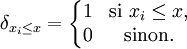
La fonction de répartition empirique est un processus qui prend ses valeurs dans l'espace des fonctions croissantes comprises entre 0 et 1. Grâce à ses propriétés, on a la convergence suivante :

$\mathbb{P}\left[ \sup_{x} |F_n(x)-F(x)|>\frac{c}{\sqrt{n}} \right]\xrightarrow[n\to\infty]{} \alpha(c)= 2\sum_{r=1}^{+\infty} (-1)^{r-1}\exp(-2r^2c^2)$

pour toute constante c > 0. Le terme α(c) vaut 0.05 pour c = 1.36. Remarquons que la limite à droite ne dépend pas de F. Cela découle du fait que 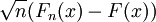$\sqrt{n}(F_n(x)-F(x))$ converge en loi vers un pont brownien changé de temps par l'inverse F ^{− 1} de F. La série α(c) se déduit des propriétés de ce dernier processus.

Il est ainsi facile de proposer un test d'hypothèse pour décider si un échantillon provient bien d'une loi donnée, ou si deux échantillons ont la même loi, lorsque leurs fonction de répartitions sont continues.

On peut aussi considérer max_x(F_n(x) − F(x)) et max_x(F(x) − F_n(x)).

Le test de Kolmogorov-Smirnov est par exemple utilisé pour tester la qualité d'un générateur de nombres aléatoires^[1].

Exemple

On illustre le test en simulant trois variables aléatoires: x et y de loi normale, z de loi uniforme. On applique ensuite le test de même distribution sur les trois paires puis le test d'adéquation à une distribution connue, en utilisant la fonction ks.test() du logiciel libre de statistiques R.

Génération de variables aléatoires x, y et z

x <- rnorm(50) #Simulation de 50 observations d'une loi normale
y <-rnorm(40)  #Simulation de 40 observations d'une loi normale
z <- runif(30) #Simulation de 30 observations d'une loi uniforme 

Test d'adéquation de distribution de deux échantillons

Test de x et y

Résultat affiché	Code R
Two-sample Kolmogorov-Smirnov test data: x and y D = 0.135, p-value = 0.7652 alternative hypothesis: two-sided	ks.test(x, y)

La probabilité que les échantillons x et y (générés par une loi normale) soient issues de la même loi aléatoire est de 0.7 (les chiffres obtenus en reproduisant l'exemple peuvent varier!).

Test de x et z

Résultat affiché	Code R
Two-sample Kolmogorov-Smirnov test data: x and z D = 0.48, p-value = 0.0002033 alternative hypothesis: two-sided	ks.test(x, z)

La probabilité que les échantillons x (généré par une loi normale) et z (généré par une loi uniforme) soient issues de la même loi aléatoire est plus petite que 0.1%, on peut donc rejeter l'hypothèse de même distribution.

Test de y et z

Résultat affiché	Code R
Two-sample Kolmogorov-Smirnov test data: y and z D = 0.55, p-value = 2.889e-05 alternative hypothesis: two-sided	ks.test(y, z)

La probabilité que les échantillons y (généré par une loi normale) et z (généré par une loi uniforme) soient issues de la même loi aléatoire est plus petite que 0.1%, on peut donc rejeter l'hypothèse de même distribution.

Test d'adéquation d'un échantillon à une distribution connue

Test si x suit une loi normale

Résultat affiché	Code R
One-sample Kolmogorov-Smirnov test data: x D = 0.0824, p-value = 0.8586 alternative hypothesis: two-sided	ks.test(x, "pnorm")

La probabilité est ici de 80%, on ne rejette donc pas l'hypothèse (qui est vraie puisque x est généré selon une loi normale) que x suit une loi normale.

Test si x suit une loi uniforme

Résultat affiché	Code R
One-sample Kolmogorov-Smirnov test data: x D = 0.5501, p-value = 1.033e-14 alternative hypothesis: two-sided	ks.test(x, "punif")

La probabilité est ici de moins de 0.01%, on rejette donc l'hypothèse (qui est fausse puisque x est généré selon une loi normale) que x suit une loi uniforme.

Voir aussi

• Andrey Kolmogorov
• Vladimir Smirnov
• tests de normalité de la loi normale
• Test de Jarque Bera
• test de Kuiper
• test de Shapiro-Wilk
• test d'Anderson-Darling
• critère de Cramér-von-Mises

Références

• (en) Galen R. Shorack et Jon A. Wellner, Empirical Processes With Applications to Statistics, John Wiley & Sons Inc, 1986, 976 p. (ISBN 047186725X).

• (en) David Williams, Weighing the Odds: a Course in Probability and Statistics, Cambridge University Press, 2001, 548 p. (ISBN 052180356X).

Notes

1. ↑ (en) Donald E. Knuth, The Art of Computer Programming, vol. 2, 3^e éd., Addison-Wesley Professional, 784 p. (ISBN 0201896842), p. 48–55.

Liens externes

• Calcul de la table de Smirnov-Kolmogorov (en anglais) : http://www.octave.org/octave-lists/archive/octave-sources.2003/msg00031.html
• Exemple de table : http://www.eridlc.com/onlinetextbook/appendix/table7.htm

Ce document provient de « Test de Kolmogorov-Smirnov ».