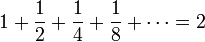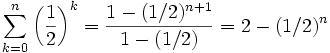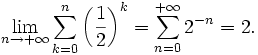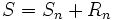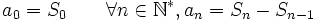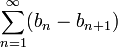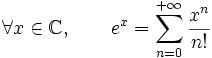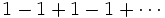- Série semi-convergente
-
Série (mathématiques)
 Pour les articles homonymes, voir Série.
Pour les articles homonymes, voir Série.En mathématiques, la série constitue une généralisation de la notion de somme, pour une succession infinie de termes. L'étude des séries consiste à effectuer la somme d'un nombre fini n de termes successifs, puis à observer le comportement lorsque n devient indéfiniment grand, par un calcul de limite. Un certain nombre de méthodes permettent de déterminer la nature (convergence ou non) des séries sans réaliser explicitement ces deux calculs.
Sommaire
Séries numériques
Une série de terme général xn est formellement le couple formé par les deux suites
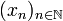 et
et 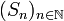
- où pour tout entier naturel n,
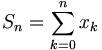
Cette suite
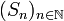 est aussi appelée la « suite des sommes partielles », puisqu'à un indice n donné, Sn fait correspondre la somme des n + 1 premiers termes de
est aussi appelée la « suite des sommes partielles », puisqu'à un indice n donné, Sn fait correspondre la somme des n + 1 premiers termes de 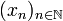 .
.Ainsi, la suite des sommes partielles associée à la série de terme général xn est de la forme :

Les séries numériques sont les séries dont les termes xn sont des nombres réels ou des nombres complexes. Il existe également des séries vectorielles, dont les termes sont des vecteurs d'un certain espace vectoriel. On peut ainsi étudier par exemple des séries de matrices ou des séries de fonctions. Leurs spécificités seront indiquées plus bas.
On note la série de terme général xn :
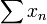 ou
ou 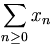 .
.Convergence
La série numérique
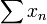 est dite convergente si la suite des sommes partielles
est dite convergente si la suite des sommes partielles 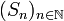 est convergente ; sa limite S est alors appelée somme de la série, elle est notée
est convergente ; sa limite S est alors appelée somme de la série, elle est notée 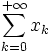 , et son calcul est la sommation de la série. Dans le cas contraire, la série est dite divergente.
, et son calcul est la sommation de la série. Dans le cas contraire, la série est dite divergente.Deux séries sont dites de même nature si elles sont toutes deux convergentes ou toutes deux divergentes.
On parle de série absolument convergente si la série de terme général | xk | est elle-même convergente (|x| signifiant ici "valeur absolue de x" si x est un nombre réel, "module de x" si x est un nombre complexe, norme s'il s'agit d'un autre élément). Si la série est convergente sans être absolument convergente, on parle de série semi-convergente.
Le fait qu'une série puisse être convergente résout beaucoup de problèmes, comme certains des paradoxes de Zénon. En revanche, il est rare qu'on sache calculer de façon explicite la somme d'une série. Hormis quelques calculs classiques, la théorie des séries a pour objectif de déterminer la nature d'une série sans calcul de la suite des sommes partielles, et éventuellement de procéder à un calcul approché de la somme.
Le terme général doit tendre vers zéro pour que la série converge. La réciproque est fausse (la série harmonique est un contre-exemple courant). Si une série ne respecte pas cette condition, on dit qu'elle diverge grossièrement.
Exemple de série
La série de terme général
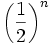 est convergente et sa somme vaut :
est convergente et sa somme vaut :Il est possible de « visualiser » sa convergence sur la droite réelle : on peut imaginer un segment de longueur 2, que l'on découpe en segments successifs de longueurs 1, 1/2, 1/4, etc. Il y a toujours assez de place pour marquer le segment suivant, parce que la longueur restante est constamment égale à la longueur du segment qui vient d'être marqué. Lorsque nous avons marqué 1/2, il reste un morceau de longueur 1/2 non marqué, ainsi nous pouvons encore certainement marquer le prochain 1/4. Cet argument ne peut en aucune façon servir de démonstration que la somme de toutes les longueurs des segments est égale à 2, mais permet de deviner que cette somme va rester inférieure à 2 et donc que la suite des sommes partielles est croissante et majorée.
Cette série est une série géométrique et on démontre sa convergence en écrivant pour tout entier naturel n, sa somme partielle au rang n :
La suite géométrique
 de raison 1/2 est convergente de limite nulle donc
de raison 1/2 est convergente de limite nulle doncReste d'une série convergente
Si la série
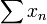 est convergente, alors pour tout entier naturel n, la somme
est convergente, alors pour tout entier naturel n, la somme 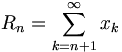 existe, et
existe, et 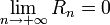 . Le terme
. Le terme  s'appelle le reste d'ordre n de la série
s'appelle le reste d'ordre n de la série 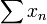 .
.Il est facile, par un procédé itératif, de calculer un terme de la suite des sommes partielles. La relation entre la somme partielle, la somme et le reste s'écrit
Ainsi, si on sait borner le reste, la somme partielle peut être vue comme une valeur approchée de la somme, avec une incertitude connue. C'est le principe du calcul numérique d'une somme de série.
Série et suite des termes généraux
Il est possible de retrouver le terme général à partir de la suite des sommes partielles par les formules
Ainsi toute somme partielle est une suite, mais toute suite est également une somme partielle (associée à la série des différences des termes consécutifs, avec un premier terme nul). Selon le cas, on aura intérêt à considérer une suite comme une somme partielle, ou inversement, selon la facilité de l'analyse des termes.
Par ailleurs, si la série
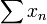 est convergente, alors la suite
est convergente, alors la suite 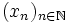 converge vers 0. La réciproque est fausse (on peut prendre la série harmonique comme contre-exemple). Lorsque le terme général d'une série ne tend pas vers 0, celle-ci est dite trivialement ou grossièrement divergente.
converge vers 0. La réciproque est fausse (on peut prendre la série harmonique comme contre-exemple). Lorsque le terme général d'une série ne tend pas vers 0, celle-ci est dite trivialement ou grossièrement divergente.Exemple :
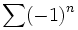 est une série grossièrement divergente, en revanche, pour
est une série grossièrement divergente, en revanche, pour 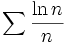 , bien que le terme général tende vers zéro, on ne peut pas trancher sans d'autres théorèmes.
, bien que le terme général tende vers zéro, on ne peut pas trancher sans d'autres théorèmes.Aspects historiques
La considération de véritables sommes infinies est une question étroitement liée à celle du passage à la limite. L'absence persistante des concepts satisfaisants engendra de nombreuses interrogations et spéculations, à l'exemple des paradoxes de Zénon.
Le mathématicien et astronome Madhava fut le premier, au XIVe siècle, à considérer de véritables séries. Ses travaux furent poursuivis par ses successeurs de l'école du Kerala, région du sud de l'Inde, et nous sont connus par le livre Yuktibhasa. Madhava s'intéresse à des fonctions trigonométriques, il en propose des développements de fonctions sous forme de séries, séries de Taylor, séries trigonométriques. Il utilise ces concepts pour des calculs d'approximation (notamment pour estimer le nombre π) et effectue des estimations de l'erreur commise. Il introduit aussi les premiers critères de convergence.
Au XVIIe siècle, James Gregory redécouvre plusieurs de ces résultats, notamment le développement des fonctions trigonométriques en séries de Taylor et la série de Gregory permettant le calcul de π. En 1715, Brook Taylor, en donnant la construction générale des séries qui portent son nom, établit un lien fructueux avec le calcul différentiel. Au XVIIIe siècle également, Leonhard Euler établit de nombreuses relations remarquables portant sur des séries et introduit les séries hypergéométriques.
Étude de la nature des séries numériques
Calculs explicites
Il est rare de pouvoir calculer explicitement tous les termes de la suite des sommes partielles.
- Les séries géométriques sont celles dont chaque terme est obtenu en multipliant le terme précédent par un nombre constant (appelé raison). La série de terme général zn est convergente si et seulement si le nombre (réel ou complexe) z vérifie :
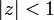 .
.
Exemples:
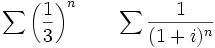 toutes deux convergentes
toutes deux convergentes- Les séries télescopiques sont de la forme
Elles sont convergentes si et seulement si la suite (bn) converge vers une limite L quand n tend vers l'infini. La valeur de la somme de la série est alors b1 - L.
Principes d'étude
Il existe un grand nombre de règles pour les séries à termes positifs. Elles sont toutes basées sur le principe de comparaison : si pour tout entier n, on a
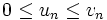 , alors
, alors- si la série
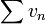 converge, la série
converge, la série 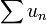 aussi ;
aussi ; - si la série
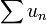 diverge, la série
diverge, la série 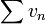 aussi.
aussi.
Pour ces séries à termes positifs, il convient donc de déterminer la nature de certaines séries de références (telles que les séries géométriques), puis de comparer à ces séries.
L'étude des séries à termes réels ou complexes, sans hypothèse particulière, peut poser plus de problèmes. Une condition suffisante a une grande importance : si la série des valeurs absolues (série à termes réels) ou des modules (séries à termes complexes)
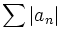 converge, alors la série
converge, alors la série 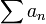 converge également. Elle est alors dite absolument convergente.
converge également. Elle est alors dite absolument convergente.Il existe des séries convergentes sans être absolument convergentes, comme la série harmonique alternée
 . Les méthodes d'étude pour ce type de série, plus techniques, (critère de convergence des séries alternées, théorème d'Abel,...) sont présentées dans :Article détaillé : Série convergente.
. Les méthodes d'étude pour ce type de série, plus techniques, (critère de convergence des séries alternées, théorème d'Abel,...) sont présentées dans :Article détaillé : Série convergente.Exemples de référence
- La série harmonique est la série :
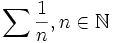 . Cette série est divergente. On montre en effet que quand
. Cette série est divergente. On montre en effet que quand 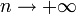 ,
,  où γ est la constante d'Euler.
où γ est la constante d'Euler.
- La série factorielle est la série : Exemple:
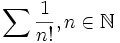 . Cette série a pour somme e, la constante de Néper.
. Cette série a pour somme e, la constante de Néper.
- Les séries de la forme :
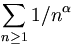 où
où 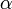 est un réel quelconque,
est un réel quelconque,
sont convergentes si et seulement si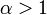 . Ces séries sont les séries de Riemann. La fonction Zeta de Riemann est la fonction qui à
. Ces séries sont les séries de Riemann. La fonction Zeta de Riemann est la fonction qui à 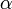 associe la somme de cette série.
associe la somme de cette série.
- Les séries de la forme :
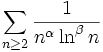 , avec
, avec 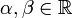 ,
,
sont convergentes si et seulement si (
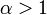 ) ou (
) ou ( et
et 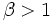 ). Ces séries sont les séries de Bertrand.
). Ces séries sont les séries de Bertrand.Séries à valeurs vectorielles
Si E est un espace vectoriel normé, une série dont les termes sont à valeurs dans E est dite convergente lorsque la suite des sommes partielles converge pour la norme choisie. Si E est de dimension finie, tous les choix de normes donneront la même notion de convergence.
Dans le cas des espaces de Banach, beaucoup de critères de convergence peuvent être énoncés, puisqu'il suffit de prouver la convergence absolue de la série pour montrer qu'elle converge. Cela permet fréquemment de conclure avec les outils d'étude des séries à termes positifs.
Plus généralement, la notion de série peut être définie dans tout groupe abélien topologique.
Séries de fonctions
Article détaillé : Série de fonctions.Formellement, les séries de fonctions sont simplement des séries dont le terme général appartient à un espace vectoriel de fonctions. Ainsi la fonction exponentielle est somme d'une série de fonctions puissances puisque
Il existe de nombreuses façons non équivalentes de définir la convergence d'une telle série, comme dans le cas des suites de fonctions. Les plus classiques sont sans doute la convergence simple et la convergence uniforme. Un grand nombre de théorèmes existent détaillant, en fonction du type de convergence, s'il est possible d'effectuer des calculs tels que dérivation ou intégration de la fonction somme d'une série.
Séries trigonométriques et séries de Fourier
Article détaillé : Série de Fourier.Les séries trigonométriques sont obtenues en sommant des fonctions sinusoïdales de fréquence n.f où f est une fréquence de référence donnée. Une question fondamentale en analyse harmonique est la possibiité de faire apparaître une fonction périodique donnée comme somme d'une série trigonométrique : sa série de Fourier.
Séries entières
Article détaillé : Série entière.La plupart des fonctions usuelles en mathématiques peuvent être représentées localement par une série de Taylor. Ce sont des séries dont le terme général s'écrit avec une puissance d'une variable ; elles sont appelées séries entières. Mais seulement dans certains cas. Exemples :
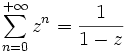
Cette série est convergente si et seulement si le nombre (réel ou complexe) z vérifie :
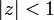 .
.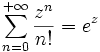
Cette série est convergente pour tout nombre réel ou complexe z.
Historiquement, les mathématiciens comme Leonhard Euler travaillaient librement avec les séries, même si celles-ci n'étaient pas convergentes. Lorsque les bases du calcul ont été solidement posées au dix-neuvième siècle, des démonstrations rigoureuses de la convergence des séries ont été exigées. Cependant, les calculs formels avec des séries (pas forcément convergentes) sont à l'origine des séries formelles dans les anneaux étudiés en algèbre générale.
Les séries formelles sont aussi utilisées en algèbre combinatoire pour décrire et étudier certaines suites, et aussi pour les fonctions génératrices.
Séries de Dirichlet
Article détaillé : Série de Dirichlet.Notion de sommes infinies
Les séries ne sont que l'exemple le plus simple de formalisation de la notion de somme infinie. Il existe d'autres définitions, plus exigeantes ou au contraire plus souples.
Les séries ne sont pas vraiment des sommes
Article détaillé : Famille sommable.Il y a dans la définition des sommes de séries convergentes un calcul de somme finie, suivi d'un passage à la limite. À cause de cette deuxième étape, l'expression « somme infinie » est incorrecte pour qualifier les séries. Une telle « somme » n'est en effet pas commutative, ni associative, ni distributive vis à vis de la multiplication. Il n'est pas possible, en général, de dériver une telle somme par rapport à un paramètre.
Les familles sommables ont des propriétés qui leur donnent beaucoup plus de titres à être qualifiées de « sommes infinies ». Alors que dans le cas des séries, on ajoute les termes dans l'ordre de succession des indices u0,u1, ... puis un, la notion de famille sommable demande d'obtenir un même résultat quel que soit l'ordre dans lequel on effectue les sommations. La propriété de commutativité par exemple est alors vraie par définition même.
Procédés de sommation des séries divergentes
Article détaillé : Série divergente.Les procédés de sommation sont des types de convergence plus faibles permettant de définir la somme de certaines séries divergentes. Par exemple le procédé de sommation de Cesàro donne pour résultat 0 lorsqu'on somme la série
Il est défini en calculant successivement les moyennes des n premiers termes de la suite des sommes partielles et en passant à la limite.
Les autres procédés de sommation les plus classiques sont la sommation d'Abel et la sommation de Borel.
Voir aussi
- Portail des mathématiques
Catégorie : Série - où pour tout entier naturel n,
Wikimedia Foundation. 2010.